【数字图像处理期末复习整理 个人】

直方图
均衡化
标准化
cdf
模板mask 三种
线性
smoothing
size
概念
sharpening mask
gradient mask

二阶一阶导数
非线性
Order-statistic filters

Chapter 4 frequency domain
fourier transforms概念、程序（数学细节不要求）
空间频率
傅里叶变换的基
系数*基
空间频率
detail
方波 谐波
formula公式
功率谱

高斯滤波器
高通低通
噪声
局部自适应滤波器
滤波效果

chapter 6 color image
色度图 理解概念
混色 主观
假彩色编码 编程
chapter7小波
统计范围有限
pyramid
entropy
冗余
度量
哈夫曼 变长编码

数字图像概述

应用领域

• Image Segmentation 图像分割
• Binary Image Operations 图像二值化
• Mathematical Morphologe 数学形态学
• Classification and Decision 分类和决策
• Image Mosaicing 图像拼接
• Image enhancement 图像增强
• Industrial Application 工业应用
• Remote Sensing 遥感
• License Plater reader 车牌读取
• Nover applications 新应用

Universities abroad 国外大学
Related areas:

• Computer vision 计算机视觉
• Virtual reality(VR) 虚拟现实
• Augmented(AR) 增强现实
• Computer graphics 计算机图形学
• Artificial intelligenc 人工智能
• Machine learning 机器学习
• Pattern recognition 模式识别
• Image processing 图像处理
• Image analysis 图像分析

图像采样和量化

1. 采样：图像在空间上的离散化（横坐标数字化）
2. 量化：把采样得到的各像素的灰度值从模拟转换到离散量（纵坐标的数字化）

计算图片存储容量

$$ImageSize=像素\times 色深bit$$

色度学基础与颜色基础

图像分辨率
每英寸图像内的像素点数，ppi
空间分辨率
空间分辨率是指图像可辨认的临界物体空间几何长度的最小极限
幅度分辨率
幅度分辨率是指幅度离散，每个像素都有一个强度值，称该像素的灰度
对比度
$对比度=最大亮度/最小亮度$

直方图

直方图均衡化

缺点：灰度级缺失

平滑滤波

• 邻域平均法
  • 变换后，大于阈值则变为新的灰度级，小于阈值则保持原灰度级
• 中值滤波法
  • 排序，取中位数
• 高斯滤波
• 消除高斯噪声
  加权平均灰度值
  线性平滑滤波

锐化

• 二阶导
  • 拉普拉斯算子
    
• 一阶导数锐化
  • 罗伯特差分法（罗伯特交叉梯度算子）
  • 梯度差分法

哈夫曼编码

阈值化分割

灰度化

1. 浮点算法：$Gray=R\times 0.3+G\times 0.59+B\times 0.11$
2. 平均值算法：$Gray=(R+G+B)/3$
3. 仅取绿色：$Gray=G$

二值化处理

1. 取阈值为127
2. 计算像素点矩阵中所有像素点的灰度平均值
3. 使用直方图法（双峰法）直方图找谷底，大于谷底取1，小于谷底取0

腐蚀与膨胀

• 腐蚀，完全对应结构元$B$则消去结构元中心点
• 膨胀，有一个对应结构元$\bar{B}$，则取结构元中心点

击中与击不中

点操作

亮度对比度矫正
$$g(i,j)=a\times f(i,j)+b$$
a修改直方图的离散程度–>a小于1，对比度降低
b使得灰度级偏移–>亮度
伽马矫正
$$o=(\frac{I}{255}{)}^{\gamma }\times 255$$
当$\gamma <1$时，原始暗区将更亮，直方图向右移动，而$\gamma >1$时相反
位平面操作（位平面切片）
图像压缩，取每个像素二进制灰度最高有效位或其他1~8位
对比度拉伸

阈值化处理Threshold

第6章 Color Image

颜色模型

• RGB： red green blue
• HSI：色调(Hue)，饱和度(Saturation)，亮度(Intensity)
• CMYK：Cyan青色，Magenta洋红色，Yellow黄色，Black黑色；印刷四分色

计算颜色模型

RGB
CIE XYZ模型
Lab模型

视觉颜色模型

HSI模型
HSV模型
HSL模型

工业颜色模型

CMYK模型
YUV模型
YCbCr模型 彩色图像压缩

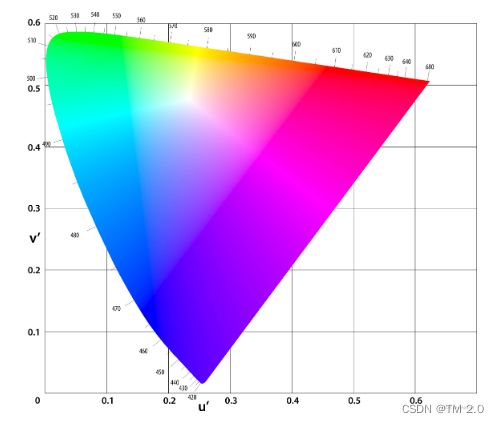
色度（色调Hue）图

伪彩色编码 Pseudo color coding

伪彩色图像处理

• 基于灰度的伪彩色编码
• 基于频域的伪彩色编码

傅里叶变换 Fourier transform

未中心化

中心化后

小波变换 Wavelet transform

缩放母小波的宽度来获得信号的频率特征，平移母小波来获得信号的时间信息。缩放和平移操作是为了计算小波系数，小波系数反映了小波和局部信号之间的相关度程度。
The frequency characteristics of the signal are obtained by scaling the width of the parent wavelet, and the time information of the signal is obtained by translating the parent wavelet. The scaling and panting operations are used to calculate the wavelet coefficients, which reflect the degree of correlation between the wavelet and the local signal.

与Fourier变换相比:小波变换是时间(空间)频率的局部化分析，它通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意节细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。有人把小波变换称为“数学显微镜”。

Chapter 1

An Introduction to the Course（课程简介）
History历史
Related Areas: Low-level, Mid-level, High-level
相关领域：低级、中级、高级
Charters of the course
课程章程
Example application: Application Areas
实例应用：应用领域
Image Segmentation
图像分割
Binary Image Operations
二进制图像操作
Mathematical Morphology
数学形态学
Classification and Decision
分类和决策
Image Mosaicing
图像拼接
Image enhancement
图像增强
Industrial Application
工业应用
Remote Sensing
遥感
Finger print image
指纹图像
License Plate reader
车牌读取器
Novel applications
新应用

Chapter 2

Topics：
话题
Universities abroad
国外大学
Major concepts
主要概念
Pixel, Matrix,
国外大学
Related areas: Computer vision, Virtual reality(VR), Augmented Reality (AR), Computer graphics, Artificial intelligence, Machine learning, Pattern recognition, Image processing, Image analysis,
相关领域：计算机视觉、虚拟现实（VR）、增强现实（AR）、计算机图形学、人工智能、机器学习、模式识别、图像处理、图像分析
Key technologies and applications
关键技术和应用
Sampling and quantification :
采样和定量：
The number of quantization levels
量化级别的数量
Digital representation of the image
图像的数字表示
Storage capacity: calculation
存储容量：计算
Human visual system & light
人类视觉系统和光线
photopic vision: cones
光视觉：圆锥体
scotopic vision: rods
暗视：视杆
brightness adaptation: subjective brightness
亮度自适应：主观亮度
visible spectrum
可见光谱
wavelength & object
波长和对象
CCD
Nyquist Sampling Theorem
抽样定理
Gray Scales
灰度
Dynamic Range
动态范围
Empirical study of resolutions
分辨率的实证研究
Isopreference curves
等距曲线
Interpolation
插值
Distance measure
测量距离
主观视觉

Chapter 3 Intensity Transformations and Spatial Filtering

第三章 强度变换和空间滤波
Topics：
Point operation:
点操作
Gray-level transformation, Gama correction, bit plane operation (Bit-plane slicing)
灰度级变换、伽马矫正、位平面操作（位平面切片）、对比度拉伸
Contrast Stretching
对比度拉伸
Threshold
阈值
Arithmetic/logic operations
算术逻辑运算
dynamic range of gray level
灰度动态范围

Histogram Processing
直方图处理
Concepts, significant & application
概念意义和应用
Normalized histogram
归一化直方图
Histogram Equalization
直方图均衡
Operation like Experiment II（Page148, example3.5）
类似实验二的操作
CDF（Cumulative Distribution Function）
累积分布

Evaluation criteria of histogram equalization: entropy
直方图均衡化的评价标准：熵
Smoothing spatial filter (mask)
平滑空间过滤器（遮罩）
Linear filters (averaging filter) : Arithmetic mean, Gaussian mean
线性滤波器（平均滤波器）：算术平均值，高斯平均值
Order-statistic filters (median filter)
顺序统计过滤（中间值过滤）
the difference between those smoothing spatial filters.。
平滑空间滤波器之间的差异
（All possible operations are required）
（需要所有可能的操作）
Size of the mask
遮罩的大小
Sharpening mask
锐化遮罩
First-Order Derivative: Gradient mask,
一阶导数|梯度掩模
Second-Order Derivative: Laplacian Operator
二阶导数：拉普拉斯算子

Chapter 4 Filtering in the Frequency Domain

频域滤波
Topics：
Image with different complexities (detail)
具有不同复杂性的图像（细节）
Global statistic for spatial frequencies
空间频率的全局统计
Mathematic foundation for Fourier transforms：
傅里叶变换的数学基础
The concepts:
概念
Spatial frequency
空间频率
Frequency domain: Why and How?
频域：
Coefficients of Fourier transform: the meaning?
傅里叶变化系数的意义
Fourier transform for image processing：
用于图像处理的傅里叶变换

短时傅里叶变换（Short-time Fourier Transform, STFT）

窗太小：频率分辨率差
窗太大：时间分辨率差
Two-Dimensional Discrete Fourier Transform
二维离散傅里叶变化
The formula:
公式
Forward transform
正向变换
Inverse transform
逆变换
Explanation for that
解释
Transformation kernel: the basis
变换内核：基
Forward transform to inverse transform
正变换到逆变换
Matlab toolbox of Fourier transform for image processing
图像处理中傅里叶变换的matlab工具
Operation steps
操作步骤
Matlab programming for frequency domain operations
频域运算的matlab编程
fft2傅里叶变换
ifft2逆傅里叶变换
fftshift Centered Representation
居中显示
ifftshift
Explanation and understand of power spectrum:
功率谱的解释和理解
relation between spatial domain and frequency domain: direction & position
空间域和频率域的关系：方向和位置
Spatial Frequency in different directions
不同方向的空间频率

Filtering in frequency domain:
频域滤波
dc component, programming
直流组件 编程
Cutoff
切断
radical cutoff: ideal filter
自由基截止：理想滤波器
smooth cutoff: Butterworth, Gaussian
平滑截止：巴特沃斯，高斯
Lowpass & highpass
Topics for research:
研究主题
What is the Fourier transform of a Gaussian ?
高斯的傅里叶变化是什么
Gaussian
高斯
Heuristically search for parameters of a Gaussian to make its Fourier transform identical to the one in time domain.
启发式搜索高斯的参数，使其傅里叶变换与时域的傅里叶变换相同
(1) As there is substantial relation between the frequency distribution and specific object feature in spatial domain, is it any possible to trace the object based on its frequency distribution in Fourier spectrum. If this is possible, present a scheme of experiment to confirm it.
由于频率分布与空间域中的特定对象特征之间存在着实质性的关系，是否有可能基于傅里叶频谱中的频率分布来跟踪对象。如果这是可能的，提出一个实验方案来证实。
(2) Observe closely on the Fourier spectra of a video. Is it possible to extract a moving object from the background by tracing the variation on their Fourier spectrum.
仔细观察视频的傅里叶光谱。通过追踪其傅里叶光谱的变化，是否可以从背景中提取运动物体。
Convolution Theorem
卷积定理

Chapter 5 Image Restoration and Reconstruction

图像恢复与重建
Topics
Noise models:
噪声模型
Spatial properties, Frequency properties, Gaussian noise, Uniform noise, Impulse (salt-and-pepper) noise
空间特征、频率特征、高斯噪声、均匀噪声、脉冲（salt-and-peper）噪声
Test for noise behavior
噪声行为测试
Restoration in the Presence of Noise Only-Spatial Filtering
纯噪声空间滤波器的恢复
Periodic Noise Reduction by Frequency Domain Filtering
利用频域滤波降低周期性噪声
Bandreject filters, Bandpass filters, Notch filters
带阻滤波器、带通滤波器、陷波滤波器
Estimation of noise parameters
噪声参数估计
Noise reduction methods for images
图像降噪方法
Adaptive noise reduction filter
自适应降噪滤波器
Adaptive local noise reduction filter: formula & programming
自适应局部降噪滤波器：公式和编程
Wiener filter: notion, formula & Matlab function (wiener2 )
维纳滤波器：概念、公式和matlab函数（wiener2）

Chapter 6 Color Image

Topics
Color models （RGB，HSI，CMYK）
颜色模型
Understand chromaticity (application questions)
了解色度（应用问题）
Saturation & Hue
饱和度和色度
Light Spectrum: visible spectrum
光谱：可见光谱
Pseudo color coding
伪彩色编码
calculation/Pseudocolor image processing
计算伪彩色图像处理
Gray scale based pseudo color coding
基于灰度的伪彩色编码
Frequency domain based pseudo color coding (wirh Programming )
基于频域的伪彩色编码

Chapter 7 Wavelets and Multiresolution Processing

小波和多分辨率处理
Topics
The notion of multiresolution
多分辨率的概念
Common features VS personalities
共同特征vs个性
Multiscale view
多尺度视图
Different scale of averaging
不同的平均尺度
Local mean and histogram
局部均值和直方图

Image Pyramids 图像金字塔

同一图像的不同分辨率的子图集合
A collection of subgraphs of the same image at different resolutions

Multiresolution concept of Pyramid金字塔的多分辨率概念

金字塔的多分辨率概念

Pyramid calculations 金字塔计算

向下取样

1. 对图像进行高斯核卷积（加权平均）
2. 删除图像的偶数行列

向上取样

1. 每个方向上扩大为原来的2倍，新增的行列用0填充
2. 使用同样的卷积核乘以4，获取新像素的新值

Approximation Pyramid: : Gaussian
近似金字塔：高斯
Prediction residual Pyramid: Laplacian
预测残差金字塔：拉普拉斯

Wavelet transforms 小波变换

Two dimension discrete image transforms in general 二维离散图像变换

二维图像离散小波变换（DWT）
Wavelet transform VS Fourier transform
小波变换vs傅里叶变换
The formula and explanations
公式和解释
Mother wavelet
母小波
Daughter wavelet
子小波
Scale and position
比例和位置
Properties
属性
Haar wavelet
哈尔小波转换
Wavelet Toolbox-wavemenu
小波工具箱波形菜单
Waveinfo

Wavelet Toolbox
小波工具箱
Programming examples
编程示例
dwt2
wavedec2
波长dec2
Image fusing and image mosaicking
图像融合和图像拼接

Chapter 8 Image compression

图像压缩
The notion of various data redundancy
各种数据冗余的概念
The notion of image compression: lossless & lossy
图像压缩的概念：无损和有损
First & higher order entropy
一阶和高阶熵
Huffman coding and RLE
哈夫曼编码与rle

short paper

1. 通过数字图像处理这门课程，我了解了图像的基本原理，如何数字化存储数字图像；通过平滑处理、锐化等方式实现图像的增强；利用傅里叶变换、小波变换等方式提取图像的特征；在课堂上，我领略到这门课程的乐趣，将之前所学的各种数学公式运用到实际的图像处理中；并且不仅仅是图像，在音频、电波等领域有许多知识也是相通的。这门课程带我进入了信号处理的大门，今后许多知识也将是在这基础之上的，受益颇深！
   Through the course of digital image processing, I learned the basic principles of images and how to digitally store digital images; The image is enhanced by smoothing and sharpening; Fourier transform and wavelet transform are used to extract image features; In the class, I learned the fun of this course, and applied various mathematical formulas learned before to the actual image processing; And it is not only images, but also a lot of knowledge in audio, radio and other fields. This course has brought me into the door of signal processing. Many knowledge in the future will also be based on this, which will benefit me a lot!
2. 麻省理工视觉实验室 在移动相机视频中，运动 分割通常使用图像平面运动来执行 像素或光流。但是，处于不同深度的物体 从相机可以表现出不同的光流，即使它们共享 相同的现实世界运动。这可能会导致深度依赖性 场景的分割。
   我们的目标是开发细分市场 对具有相似真实世界运动的像素进行聚类的算法 无论它们在场景中的深度如何。
   我们的解决方案使用光学 流向而不是完整的向量并利用 众所周知的属性，在相机平移下，光流 方向与对象深度无关。
   我们介绍一个 自动估计 观察到的独立运动并导致标记 与场景中的真实世界运动一致。
   我们的结果 系统是静态对象被正确标识为一个段， 即使它们在不同的深度。
   Computer Vision Lab of Massachusetts Institute of Technology
   Professor Erik G. Learned-Miller
   Coherent Motion Segmentation in Moving Camera Videos using Optical Flow Orientations
   In moving camera videos, motion segmentation is commonly performed using the image plane motion of pixels, or optical flow. However, objects that are at different depths from the camera can exhibit different optical flows even if they share the same real-world motion. This can cause a depth-dependent segmentation of the scene.
   The goal is to develop a segmentation algorithm that clusters pixels that have similar real-world motion irrespective of their depth in the scene.
   The solution uses optical flow orientations instead of the complete vectors and exploits the well-known property that under camera translation, optical flow orientations are independent of object depth.
   The probabilistic model that automatically estimates the number of observed independent motions and results in a labeling that is consistent with real-world motion in the scene.
   The result of The system is that static objects are correctly identified as one segment, even if they are at different depths.
3. 数字图像应用