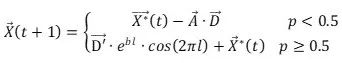【布局优化】基于鲸鱼算法实现3D无线传感器网(WSN)覆盖优化 Matlab源码
一、WSN模型
1.1 动机
近年来,随着对等网络、云计算和网格计算等分布式环境的发展,无线传感器网络(WSN)得到了广泛的应用。无线传感器网络(WSN)是一种新兴的计算和网络模式,它可以被定义为一个由称为传感器节点的微小、小型、昂贵和高度智能化的设备组成的网络。传感器节点位于被观测空间内的不同位置,通过无线通信信道交换从监测领域收集的数据。收集的数据被发送到sink节点,sink节点要么本地处理数据,要么将数据发送到处理能力更强的其他网络。
无线传感器网络最基本的挑战之一是节点定位。节点定位问题的实例很多,属于NP难优化问题。传统的确定性技术和算法不能在合理的计算时间内解决NP-hard问题。在这种情况下,最好采用非确定性(随机)算法,如元启发式算法。
群体智能元启发式算法模拟自然界中的生物群体,如鸟和鱼的群体、蜜蜂和蚂蚁的群体、蝙蝠和杜鹃鸟的群体等。这些算法是基于种群的、随机的和迭代的搜索方法,基于四个自组织原则:正反馈、负反馈,多重相互作用和波动。
1.2 无线传感器网络中的定位问题
定位问题是无线传感器网络中研究最多的问题之一,因为如果传感器节点的位置未知,则覆盖、功率和路由都将无法确定最佳。定位是无线传感器网络的关键。一些传感器节点的位置可以由全球定位系统(GPS)来定义,这些节点被称为锚节点或信标节点,而其他传感器节点则随机分布在搜索空间中。这些节点称为未知节点或传感器节点。由于每个节点的电池寿命、成本、气候条件等因素,只有少数节点的位置是由GPS坐标确定的,而其他节点的位置则需要采用定位算法进行估计。
针对无线传感器网络中传感器节点的定位问题,提出了锚节点和未知节点两种定位算法。第一阶段称为测距阶段,算法确定未知节点和相邻锚节点之间的距离。针对无线传感器网络中传感器节点的定位问题,提出了锚节点和未知节点两种定位算法。第一阶段称为测距阶段,算法确定未知节点和相邻锚节点之间的距离。第二阶段通过在第一阶段使用各种方法收集测距信息来估计节点的位置,如到达角(AOA)、到达时间(TOA)、到达时差(TDOA)、往返时间(RTT)、无线信号强度(RSS)等。
1.3 问题陈述
在由M个传感器节点组成的无线传感器网络中,定位问题的目标是利用M-N个锚节点的位置信息,在传输范围为R的情况下,估计N个未知节点的位置,如果一个传感器节点在三个或更多锚节点的传输范围内,则认为它是定位的。这是一个总坐标数为2n的二维定位问题。
本文采用RSS方法估计节点间距离。无论采用何种测距方法,都可能出现不精确的测量。N个未知节点坐标的位置估计可以表示为一个优化问题,涉及表示节点定位误差的目标函数的最小化[19]。该问题的目标函数由N个未知节点和M N个相邻锚节点之间的误差平方和表示[19]。
随着RSS的出现,三边测量将被用来解决WSN中的定位问题。该方法的原理是基于三个锚节点的已知位置。未知节点的位置可以在三个锚节点的传输范围内估计。
每个节点估计到第i个锚点的距离为d̂=di+ni,其中ni是高斯噪声,di是使用以下等式计算的实际距离:
应最小化的目标函数表示为计算节点坐标的实际和估计距离与实际节点坐标之间的均方误差(MSE):
其中di是实际距离,d̂i是估计距离(从噪声范围测量获得的值di),M≥3(传感器节点的位置在传输范围R内至少需要三个锚)。
由于节点定位中的距离测量是有噪声的,为了估计节点之间的足够距离,采用了群体智能元启发式等优化方法。
二、鲸鱼算法
2.1. 鲸鱼优化算法的生物机制
图1 座头鲸的泡泡捕食示意图
据研究,鲸鱼大脑的某些区域有与人类相似的梭形细胞,而这些细胞负责人类的判断、情感和社会行为。鲸鱼的这种细胞数量是成年人类的两倍,这是它们聪明的主要原因。事实证明,鲸能像人类一样思考、学习、判断、交流,甚至变得情绪化,但显然它的智能水平要低得多。
据观察,鲸鱼(主要是虎鲸)也能发展自己的方言。而座头鲸最有趣的地方是它们特殊的捕猎方法。这种觅食行为被称为泡泡网觅食法。座头鲸喜欢在接近海面的地方捕食磷虾或小鱼。据观察,这种觅食是通过沿着一个圆圈或“9”形路径创造独特的气泡来完成的,如图1所示。在2011年之前,这一行为仅仅是基于在地表的观察进行研究。后来利用传感器展开了更深入的研究,他们捕获了9头座头鲸的300个标签衍生的泡泡网进食事件。他们发现了两个与气泡有关的动作,并将它们命名为“向上螺旋”和“双环”。在前一种策略中,座头鲸会向下潜水12米,然后开始在猎物周围制造一个螺旋形的气泡,再游向水面。值得一提的是,泡泡网捕食是一种独特的行为,只能在座头鲸身上观察到。本文介绍如何利用螺旋泡沫网捕食机制进行数学建模,以达到优化的目的。
2.2. 数学模型与优化算法
1)对猎物的环绕
座头鲸能够识别猎物的位置并将其包围。由于优化设计在搜索空间中的位置不是先验已知的,因此WOA算法假设当前的最佳候选解是目标猎物或接近最优解。在定义了最佳搜索个体之后,其他搜索个体将尝试向最佳搜索个体更新它们的位置。这一行为由以下方程表示:
其中t表示当前迭代,![]() 和
和![]() 是系数向量,X*是目前得到的最佳解的位置向量,
是系数向量,X*是目前得到的最佳解的位置向量,![]() 为位置向量,| |为绝对值,•为逐元素乘法。这里值得一提的是,如果存在更好的解决方案,那么应该在每次迭代中更新X。
为位置向量,| |为绝对值,•为逐元素乘法。这里值得一提的是,如果存在更好的解决方案,那么应该在每次迭代中更新X。
向量![]() 和
和![]() 计算方法如下:
计算方法如下:
![]() (3)
(3)
![]() (4)
(4)
这里 ![]() 在迭代过程中(勘探和开发阶段)从2到0是线性递减的,
在迭代过程中(勘探和开发阶段)从2到0是线性递减的, ![]() 是[0,1]中的一个随机向量。
是[0,1]中的一个随机向量。
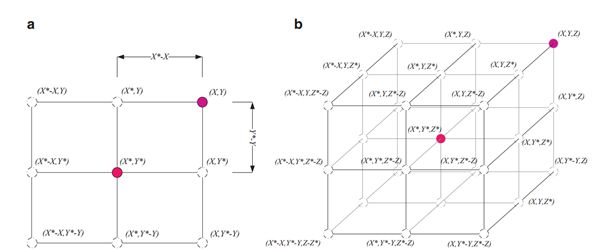
图2 二维和三维位置向量及其可能的下一个位置 (其中X*是目前获得的最佳解决方案)
图2(a)结合一个二维问题说明了公式(2)背后的原理。搜索个体的位置(X,Y)可以根据当前最佳记录的位置(X*,Y*)进行更新。围绕最佳个体的不同位置可以通过调整 ![]() 和
和 ![]() 向量来得到。图2(b)还描述了搜索在三维空间中可能的更新位置。需要注意的是,通过定义随机向量,可以到达图2所示关键点之间的搜索空间中的任意位置。因此式2允许任何搜索个体更新其在当前最佳解附近的位置,并模拟包围猎物。同样的概念可以扩展到n维的搜索空间,搜索个体将在超立方体中移动,以获得迄今为止最好的解决方案。
向量来得到。图2(b)还描述了搜索在三维空间中可能的更新位置。需要注意的是,通过定义随机向量,可以到达图2所示关键点之间的搜索空间中的任意位置。因此式2允许任何搜索个体更新其在当前最佳解附近的位置,并模拟包围猎物。同样的概念可以扩展到n维的搜索空间,搜索个体将在超立方体中移动,以获得迄今为止最好的解决方案。
2)泡泡网攻击方法
为了建立座头鲸泡泡网行为的数学模型,设计了下面两种方法:
(1) 收缩包围机制:这种行为是通过减少式(3)中的 ![]() 来实现,
来实现, ![]() 也因此变成(-a, a)之间的一个随机量,a在迭代过程中从2减到0。设置随机值
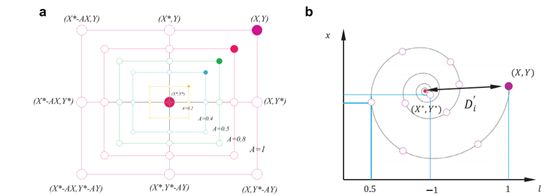
也因此变成(-a, a)之间的一个随机量,a在迭代过程中从2减到0。设置随机值 ![]() 在[- 1,1]中,搜索个体的新位置可以定义为介于原个体位置和当前最佳个体位置之间的任何位置。图3(a)显示了在二维空间中0≤a≤1可以实现从(X,Y)变到(X*,Y*)的可能位置。
在[- 1,1]中,搜索个体的新位置可以定义为介于原个体位置和当前最佳个体位置之间的任何位置。图3(a)显示了在二维空间中0≤a≤1可以实现从(X,Y)变到(X*,Y*)的可能位置。
(2) 螺旋更新位置:如图3(b)所示,这种方法首先计算位于(X,Y)的鲸鱼和位于(X,Y,Y)的猎物之间的距离。然后在鲸鱼和猎物的位置之间建立一个螺旋方程,模拟座头鲸的螺旋形运动如式(5):
![]() (5)
(5)
这里 ![]() 表示第i条鲸到猎物的距离(目前得到的最佳解),b为对数螺旋形状的常数,l为[- 1,1]中的随机数, 是一个元素对元素的乘法。
表示第i条鲸到猎物的距离(目前得到的最佳解),b为对数螺旋形状的常数,l为[- 1,1]中的随机数, 是一个元素对元素的乘法。
图3 bubbly -net搜索机制在WOA中实现(X是目前获得的最佳解决方案)
(a)收缩环绕机制 (b)螺旋更新位置
座头鲸在一个逐步缩小的圆圈内绕着猎物游动,同时沿着螺旋形的路径游动。为了模拟这种同时发生的行为,我们假设有50%的概率可以在缩小的包围机制和螺旋模型之间做出选择,以更新鲸鱼的位置。模型如下:
其中 ![]() 是一个随机数。
是一个随机数。
3)搜寻猎物(勘探阶段)
座头鲸是根据彼此的位置随机搜索的。随机计算出的 ![]() 比-1小或比1大时,将强迫搜索个体远离参考鲸鱼。相对于开发阶段,我们根据随机选择的搜索个体来更新搜索代理在探索阶段的位置,而不是根据找到的最佳搜索个体,这一机制将使WOA可进行全局搜索。此时的数学模型为:
比-1小或比1大时,将强迫搜索个体远离参考鲸鱼。相对于开发阶段,我们根据随机选择的搜索个体来更新搜索代理在探索阶段的位置,而不是根据找到的最佳搜索个体,这一机制将使WOA可进行全局搜索。此时的数学模型为:
这里 ![]() 是随机一头鲸对应的随机位置,图4画出了
是随机一头鲸对应的随机位置,图4画出了 ![]() 时特殊解的一些可能位置。
时特殊解的一些可能位置。
图4WOA算法中的勘探机制(X*是随机值)
WOA算法从一组随机解开始。在每次迭代中,搜索个体根据随机选择的搜索个体或者获得的最佳解更新其位置,将a参数由2逐步减为为0,以支持勘探和开发。当 ![]() 时,将选择一个随机的搜索个体;
时,将选择一个随机的搜索个体; ![]() 时,将选择最优解作为搜索个体。
时,将选择最优解作为搜索个体。
根据p的值,WOA可以在螺旋运动和圆形运动之间进行切换,当满足终止准则时终止WOA算法
三、代码
%% 清除环境变量
clear
clc
%% 网络参数
L = 50; % 区域边长
V = 35; % 节点个数
Rs = 5; % 感知半径
Rc = 10; % 通信半径
Re = 0.1; % 感知误差
data = 1; % 离散粒度
%% SSA参数
N = 30; % 种群规模
dim = 2*V; % 维数
ub = L;
lb = 0;
Max_iter = 300;
% 初始化节点位置
X = rand(N, dim).*(ub-lb)+lb;
% 计算适应度值
for i = 1:N
fitness(i) = fun(X(i, :), L, Rs, Re, data);
end
% 初始化领导者的位置和适应度值
[bestfitness, bestindex] = max(fitness);
gbest= X(bestindex, :);
fitnessgbest = bestfitness;
num2str(fitnessgbest)]);
end
%% 结果显示
x = gbest(1:2:end);
y = gbest(2:2:end);
disp('最优位置:' );
for i = 1:V
disp([num2str(x(i)), ' ', num2str(y(i))]);
end
disp(['最优覆盖率:', num2str(fitnessgbest)]);
%% 绘图
figure;
plot(Curve, 'r', 'lineWidth', 2); % 画出迭代图
title('WOA覆盖率进化曲线', 'fontsize', 12);
xlabel('迭代次数', 'fontsize', 12);
ylabel('网络覆盖率', 'fontsize', 12);
figure
for i = 1:V
axis([0 ub 0 ub]); % 限制坐标范围
sita = 0:pi/100:2*pi; % 角度[0, 2*pi]
hold on;
fill(x(i)+Rs*cos(sita), y(i)+Rs*sin(sita), 'k');
end
plot(x, y, 'r+');
title 'SSA优化覆盖';
![]()
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.