Multi-class Classification
1.Problem
本实验中,你将用logistic regression来识别手写数字体(0到9),由于MATLAB中的向量的索引是从1开始的,所以为了本实验方便,将数字0映射为数字10,数字1到数字9均保持不变。
1.1.Dataset
There are 5000 training examples in ex3data1.mat, where each training example is a 20 pixel by 20 pixel grayscale image of the digit. Each pixel is represented by a floating point number indicating the grayscale intensity at that location. The 20 by 20 grid of pixels is “unrolled” into a 400-dimensional vector. Each of these training examples becomes a single row in our data matrix X. This gives us a 5000 by 400 matrix X where every row is a training example for a handwritten digit image.
矩阵X可以写成:
1.2 Visualizing the data
In Part 1 of ex3.m,the code randomly selects selects 100 rows from X and passes those rows to thedisplayData function. This function maps each row to a 20 pixel by
20 pixel grayscale image and displays the images together. We have provided thedisplayData function, and you are encouraged to examine the code to see how it works. After you run this step, you should see an image like Figure
1.3 Vectorizing Logistic Regression
Since there are 10 classes, you will need to train 10 separate logistic regression classifiers. To make this training efficient, it is important to ensure that your code is well vectorized. In this section, you will implement a vectorized version of logistic regression that does not employ any for loops. You can use your code in the last exercise as a starting point for this exercise.
由于下面的内容较多,我直接截屏了哈:
function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with
%regularization
% J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
% efficiently vectorized. For example, consider the computation
%
% sigmoid(X * theta)
%
% Each row of the resulting matrix will contain the value of the
% prediction for that example. You can make use of this to vectorize
% the cost function and gradient computations.
%
% Hint: When computing the gradient of the regularized cost function,
% there're many possible vectorized solutions, but one solution
% looks like:
% grad = (unregularized gradient for logistic regression)
% temp = theta;
% temp(1) = 0; % because we don't add anything for j = 0
% grad = grad + YOUR_CODE_HERE (using the temp variable)
%
temp = theta;
temp(1,:) = 0; % because we don't add anything for j = 0
grad=1/m*X'*(sigmoid(X*theta)-repmat(y,1,size(theta,2)))+lambda/m*temp;%X:5000.400+1 theta: 400+1 10 y:5000 1
J=-1/m*y'*sum(log(sigmoid(X*theta)),2)-1/m*(ones(size(y'))-y')*sum(log(ones(size(X*theta))-sigmoid(X*theta)),2)+lambda/(2*m)*sum(sum(temp.*temp));%一定要注意theta和temp的区别
% =============================================================
grad = grad(:);
end
对应的MATLAB代码如下:
function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta
%corresponds to the classifier for label i
% [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
% logisitc regression classifiers and returns each of these classifiers
% in a matrix all_theta, where the i-th row of all_theta corresponds
% to the classifier for label i
% Some useful variables
m = size(X, 1);
n = size(X, 2);
% You need to return the following variables correctly
all_theta = zeros(num_labels, n + 1);%此处定义的theta为行向量啊,最好转置一下对应与列向量
% Add ones to the X data matrix
X = [ones(m, 1) X];
% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the following code to train num_labels
% logistic regression classifiers with regularization
% parameter lambda.
%
% Hint: theta(:) will return a column vector.
%
% Hint: You can use y == c to obtain a vector of 1's and 0's that tell use
% whether the ground truth is true/false for this class.
%
% Note: For this assignment, we recommend using fmincg to optimize the cost
% function. It is okay to use a for-loop (for c = 1:num_labels) to
% loop over the different classes.
%
% fmincg works similarly to fminunc, but is more efficient when we
% are dealing with large number of parameters.
%
% Example Code for fmincg:
%
% % Set Initial theta
% initial_theta = zeros(n + 1, 1);
%
% % Set options for fminunc
% options = optimset('GradObj', 'on', 'MaxIter', 50);
%
% % Run fmincg to obtain the optimal theta
% % This function will return theta and the cost
% [theta] = ...
% fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
% initial_theta, options);
%
% Set Initial theta
initial_theta = zeros(n + 1, 1);
% Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 50);
% Run fmincg to obtain the optimal theta
% This function will return theta and the cost
for c=1:num_labels
theta(c,:) = ...
fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
initial_theta, options);
end
all_theta=theta;
end
1.5 Predit result:
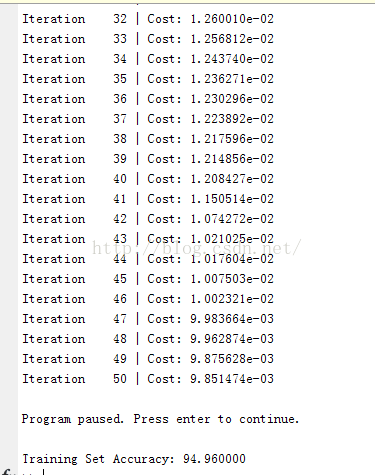
Once you are done, ex3.m will call your predictOneVsAll function using the learned value of Θ. You should see that the training set accuracy is about 94.9% (i.e., it classifies 94.9% of the examples in the training set correctly).
对应的MATLAB代码如下:
function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels
%are in the range 1..K, where K = size(all_theta, 1).
% p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
% for each example in the matrix X. Note that X contains the examples in
% rows. all_theta is a matrix where the i-th row is a trained logistic
% regression theta vector for the i-th class. You should set p to a vector
% of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
% for 4 examples)
m = size(X, 1);
num_labels = size(all_theta, 1);
% You need to return the following variables correctly
p = zeros(size(X, 1), 1);
% Add ones to the X data matrix
X = [ones(m, 1) X];
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
% your learned logistic regression parameters (one-vs-all).
% You should set p to a vector of predictions (from 1 to
% num_labels).
%
% Hint: This code can be done all vectorized using the max function.
% In particular, the max function can also return the index of the
% max element, for more information see 'help max'. If your examples
% are in rows, then, you can use max(A, [], 2) to obtain the max
% for each row.
%
[val,p]=max(X*all_theta',[],2);
end
最终运行结果为:
本博客配套的完整代码链接:http://download.csdn.net/detail/zhe123zhe123zhe123/9545997