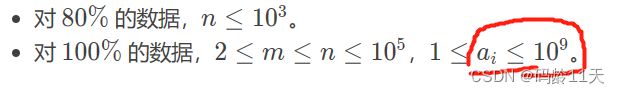洛谷2月普及组(月赛)
小宇(治愈版) - 刘大拿 - 单曲 - 网易云音乐
OI赛制且难度对标蓝桥杯省赛(真难,第三题做了几百年,第四题只敢骗骗分)
花了10块钱 买官网的思路,结果还是习惯自己硬磕,别人的思路根本不想看,还不如自己百度
切记切记,OI赛制是部分分 + 无反馈
所以骗分很重要
骗分 = 样例 + 模拟 + 暴力
养成先测试再提交的好习惯,否则,你以为你天王盖地虎,原来是个二百五
总结
总结写在前头
1,骗分 = 样例 + 模拟 + 暴力
2,不论是codeforces还是洛谷,只做对样例,不给分,盲猜改革后的蓝桥杯也没分
3,不论是codeforces还是洛谷,凡是和数字有关的,都和奇偶数规律有着千丝万缕的关系
4,第三题,AC 100%需要(邻接表 + STL的priority_queue + Dijkstra),我还有邻接表没学,先留个坑,日后有时间回来做
目录
总结
一,P9063 [yLOI2023] 分解只因数
解法1 AC 100%
解法2 AC 90%
解法3 AC 60%
二,P9064 [yLOI2023] 苦竹林
AC 30%
AC 100%
三,P9065 [yLOI2023] 云梦谣
AC 5%
四,P9066 [yLOI2023] 腐草为萤
AC 5%
一,P9063 [yLOI2023] 分解只因数
P9063 [yLOI2023] 分解只因数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
通过率 10%
难度:入门
首先要理解n不一定需要相乘得到的,比如 11 == 11,3 == 3,也可以是等本身,所以3和11也是只因数,一开始钻牛角尖了
解法1 AC 100%
因数中只要存在偶数,也就是不全为奇数,累乘的n就是偶数
所以,当n是偶数,说明质因数中存在偶数;当n是奇数,质因数全为奇数
所以n是奇数时输出"Yes",n是偶数时输出"No"
#include
#include //scanf()
using namespace std;
typedef long long LL;
bool check(LL n)
{
if(n % 2 == 1) return true;
return false;
}
int main()
{
int t;
scanf("%d", &t);
while(t) {
LL n;
scanf("%lld", &n);
if(check(n)) cout<<"Yes"< 5
2
No
3
Yes
4
No
6
No
9
Yes
4
12
No
123
Yes
1234
No
12345
Yes
解法2 AC 90%
常规解法,对质数,因数不熟练的新手,耗时比较久,比如我
质数:能被1和本身整除的数
1,遍历到m的平方差,即 i * i <= m
2,m % i == 0,则 m 不是质数
#include
#include //scanf()
using namespace std;
typedef long long LL;
bool check(LL n)
{
int flag = 1;
if(n == 1 || n == 2) return false; //1不是质数, 2是偶数
int m;
for(m = 2; m * m <= n; ++m) {
for(int i = 2; i * i <= m; ++i)
if(m % i == 0) {
flag = 0; //m不是质数
break;
}
if(flag && n % m == 0) //m是质数且是n的因子
if(m % 2 == 0) return false; //因子是偶数
}
return true;
}
int main()
{
int t;
scanf("%d", &t);
while(t) {
LL n;
scanf("%lld", &n);
if(check(n)) cout<<"Yes"< 第10个样例,Time Limit Exceeded,TLE了
输入3,由于 m * m <= 3连 m = 2都不满足,所以没经过判断,直接return true;了
解法3 AC 60%
投机取巧,骗分的方法,关键是快!只用了5分钟,分也不少
#include
#include //scanf()
using namespace std;
typedef long long LL;
bool check(LL n)
{
if(n == 2 || n == 4 || n == 6
|| n == 8 || n == 10 || n == 12 || n == 14
|| n == 16 || n == 18 || n == 20)
return false;
if(n == 3 || n == 5 || n == 9 || n == 15 || n == 21
|| n == 7 || n == 11 || n == 13 || n == 17 || n == 19)
return true;
}
int main()
{
int t;
scanf("%d", &t);
while(t) {
LL n;
scanf("%lld", &n);
if(check(n)) cout<<"Yes"< 二,P9064 [yLOI2023] 苦竹林
P9064 [yLOI2023] 苦竹林 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
通过率 14%
难度:普及-
1,先对数组a从小到大排序
2,尺取法,对连续的m个数遍历,每次更新Min
将Min与 (尺取的最后一个元素 - 尺取的第一个元素) 作比较
复杂度O(logn + n - m) ;logn表示log2n,是快排的复杂度
不会尺取法的看这里
尺取法(图文解析、初学推荐)_小白小郑的博客-CSDN博客_尺取法
算法基础----尺取法(双指针)_jkaliang的博客-CSDN博客
1,尺取法是算法竞赛中,常用的优化技巧
2,它比暴力枚举区间的效率高很多(特别是数据量大时,比如10^6),是一种高效枚举区间的方法,用于求取有一定限制的区间个数或最短区间
3,本题中通过左边界右移,右边界右移的方法,找到满足区间,并用Min保留相减最小值(也就是题目中的ε)
注意!!!OI赛制没有反馈,所以首先要自己想多点全面,偏门的案例
来验证代码,不然很可能就是信心满满 = AC 30%
先别急着提交,下面我展示5组测试样例
10 6
1 8 26 33 41 17 102 27 11 5
22
6 2
1 4 9 12 13 15
1
5 3
1 2 3 4 5
2
6 4
1 7 8 3 4 6
4
10 4
120 240 550 1101 1199 2012 3312 5520 5523 5524
959
然后,,,第一次30%
AC 30%
#include
#include //scanf()
#include //sort()
using namespace std;
int a[100010];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i)
scanf("%d", &a[i]); //读入数据
sort(a, a + n);
int Min = 1e8; //大坑
for(int i = m - 1; i < n; ++i) {
int j = i - (m - 1); //此时[j, i]刚好m个数
if(a[i] - a[j] < Min)
Min = a[i] - a[j];
}
cout< 思路很清晰啊,怎么会错呢?原来是第13行,初始最小值设置成1e8了
而题目原文却是:
所以,设置最小值,直接将题目中的范围粘贴过来好了。。
最大值一般设为负数
毕竟70%的样例都是大于1e8的
AC 100%
#include
#include //scanf()
#include //sort()
using namespace std;
int a[100010];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i)
scanf("%d", &a[i]); //读入数据
sort(a, a + n);
int Min = 1e9; //大坑
for(int i = m - 1; i < n; ++i) {
int j = i - (m - 1); //此时[j, i]刚好m个数
if(a[i] - a[j] < Min)
Min = a[i] - a[j];
}
cout< 复杂度O(n * logn),也就是快排的复杂度,后面的O(n - m)相比O(nlogn)可忽略
三,P9065 [yLOI2023] 云梦谣
P9065 [yLOI2023] 云梦谣 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目有点长,通过率 6%
难度:普及+/提高
1,读入数据较多,我们用scanf不用cin
2,点与点之间路径一样,都为1,我觉得用dfs比Dijkstra好做
所以就是纯dfs(后面证明dfs❌)
然鹅。。第一次就AC 5% ,而且我四个测试样例都对了,,,,
AC 5%
#include
#include //scanf()
using namespace std;
int a[3010][3010], book[3010][3010], b[3010][3010];
int fly[3010][3010], ans = 3000;
int n, m, k;
void dfs(int x, int y, int step)
{
int next[4][2] = { //方向数组, 循环得到下一步坐标
{-1, 0}, //上
{1, 0}, //下
{0, -1}, //左
{0, 1}}; //右
//dfs第一步: 遍历
int tx, ty; //临时变量
for(int i = 0; i < 4; ++i) {
tx = x + next[i][0]; //0表示每行第1个元素
ty = y + next[i][1]; //1表示每行第2个元素
//越界
if(tx < 1 || ty < 1 || tx > n || ty > m)
continue; //跳出本次循环
//非障碍物且未走过
if(a[tx][ty] != 0 && book[tx][ty] != 1) {
book[tx][ty] = 1; //标记
dfs(tx, ty, step + 1); //递归
book[tx][ty] = 0; //取消标记
}
}
//找到目标
if(x == n && y == m) {
ans = min(ans, step); //更新
return; //返回上一步
}
}
int main()
{
scanf("%d%d%d", &n, &m, &k);
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]); //读入数据
int r, t;
for(int i = 0; i < k; ++i) {
scanf("%d%d", &r, &t);
fly[r][t] = 1; //可飞行
}
book[1][1] = 1; //初始已走过
//得到全程走的最小值
dfs(1, 1, 0);
//得到飞的最小值
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
if(fly[i][j] == 1) { //可飞
if(a[i][j] != a[1][1]) //高度不同
dfs(i, j, 2);
else //高度一样
dfs(i, j, 1);
}
cout< 做了2小时才AC 5%,,,666
问题在哪呢?
1,dfs就不适合最短路(指数级复杂度),一般用Dijksta的堆优化求单源最短路
2,漏了,如果到达不了,要输出"-1"的情况(补上这个就AC 10%)
3,代码里默认(1, 1)能飞,这是错误的
因为只是样例中的(1, 1)能飞,存在(1, 1)不能飞,走几步才能飞的情况
最后的
cout<改成
if(ans == 3000) cout<<-1;
else cout<就AC 10%
好的,下一步考虑用stl的优先队列priority_queue优化Dijkstra
这已经是最简单的做法了,如果能成,估计只需要60行
不行了,堆优化的Dijkstra虽然可以用stl的最大最小值优先队列(大小根堆),但是还得学习什么“链式前向星”(也就是静态的邻接表),《啊哈算法》里有讲邻接表,但是我想先放放,先把简单的,更易拿分的掌握了,两个月以内再回来克服它
2023/02/12
10:27留坑
四,P9066 [yLOI2023] 腐草为萤
P9066 [yLOI2023] 腐草为萤 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
难度:提高+/省选-
题目就不放了,感兴趣的,自己去模拟 + 样例骗分吧
AC 5%
#include
using namespace std;
int a[110], b[110];
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; ++i)
cin>>a[i]; //初始位置
for(int i = 0; i < n; ++i)
cin>>b[i]; //亮度
for(int i = 1; i < n; ++i) {
if(b[i] > b[i - 1])
cout<