java常见算法-蓝桥杯每日一题冲刺国赛
1.
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例 1:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
示例 2:
输入:nums = [0,0,0], target = 1
输出:0
import java.util.Arrays;
class Soluion {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int n = nums.length;
int best = 10000000;
// 枚举 a
for (int i = 0; i < n; ++i) {
// 保证和上一次枚举的元素不相等
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
// 使用双指针枚举 b 和 c
int j = i + 1, k = n - 1;
while (j < k) {
int sum = nums[i] + nums[j] + nums[k];
// 如果和为 target 直接返回答案
if (sum == target) {
return target;
}
// 根据差值的绝对值来更新答案
if (Math.abs(sum - target) < Math.abs(best - target)) {
best = sum;
}
if (sum > target) {
// 如果和大于 target,移动 c 对应的指针
int k0 = k - 1;
// 移动到下一个不相等的元素
while (j < k0 && nums[k0] == nums[k]) {
--k0;
}
k = k0;
} else {
// 如果和小于 target,移动 b 对应的指针
int j0 = j + 1;
// 移动到下一个不相等的元素
while (j0 < k && nums[j0] == nums[j]) {
++j0;
}
j = j0;
}
}
}
return best;
}
}
2.
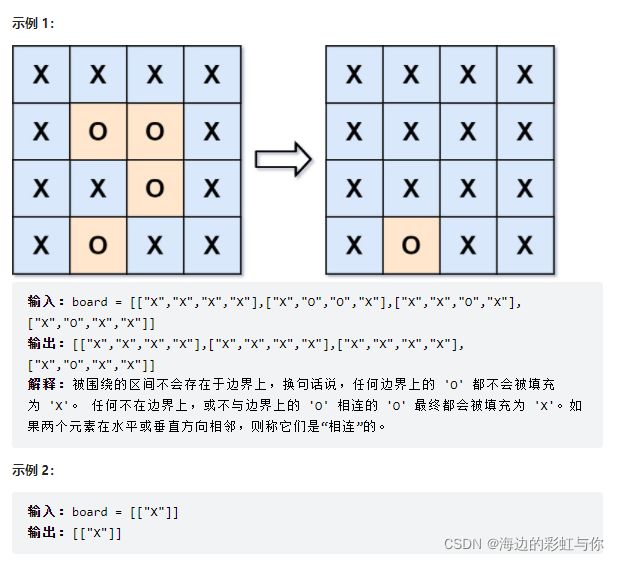
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
class Solution {
int m,n;
public void solve(char[][] board) {
n = board.length;
if (n == 0)
return;
m = board[0].length;
for (int i = 0; i < n; i++) {
dfs(i,0,board);
dfs(i,m-1,board);
}
for (int i = 1; i < m-1; i++) {
dfs(0,i,board);
dfs(n-1,i,board);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'A')
board[i][j] = 'O';
else if (board[i][j] == 'O')
board[i][j] = 'X';
}
}
}
public void dfs(int i,int j,char[][] board) {
if (i < 0 || j < 0 || i >= n || j >= m || board[i][j] != 'O')
return;
board[i][j] = 'A';
dfs(i+1,j,board);
dfs(i-1,j,board);
dfs(i,j+1,board);
dfs(i,j-1,board);
}
}3.
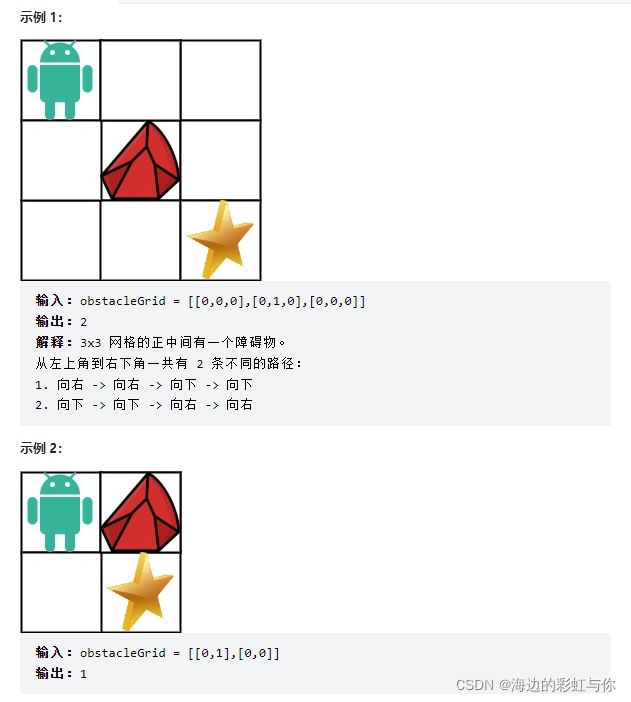
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int len1 = obstacleGrid.length;
int len2 = obstacleGrid[0].length;
int[][] dp = new int[len1][len2];
for (int i = 0; i < len2; i++) {
if (obstacleGrid[0][i] == 1)
break;
dp[0][i] = 1;
}
for (int i = 0; i < len1; i++) {
if (obstacleGrid[i][0] == 1)
break;
dp[i][0] = 1;
}
for (int i = 1; i < len1; i++) {
for (int j = 1; j < len2; j++) {
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
continue;
}
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[len1 - 1][len2 - 1];
}
}4.
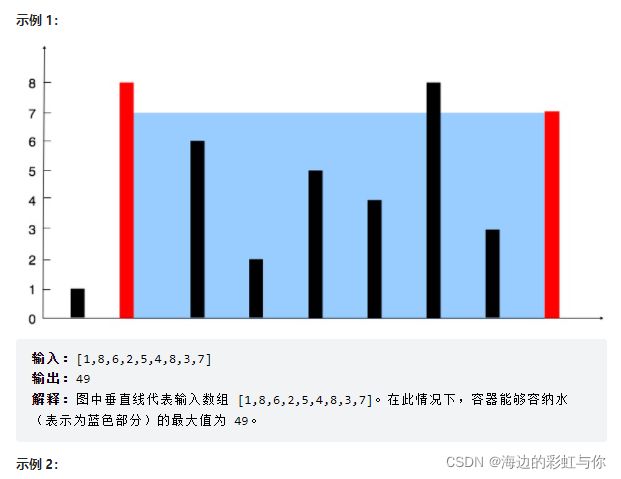
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
class Solution {
public int maxArea(int[] height) {
int len = height.length;
int res = 0;
int i = 0;
int j = len - 1;
while(i < j) {
int ans = Math.min(height[i],height[j]) * (j - i);
res = Math.max(res,ans);
if(height[i] <= height[j])
i++;
else
j--;
}
return res;
}
}5.
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
class Solution {
public void nextPermutation(int[] nums) {
int len = nums.length;
int i = len - 2;
while (i >= 0 && nums[i] >= nums[i + 1])
i--;
if (i >= 0) {
int j = len - 1;
while ( j > 0&&nums[j] <= nums[i] )
j--;
swap(i,j,nums);
}
reserve(i + 1,nums);
}
public void swap(int i,int j,int[] nums) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
public void reserve(int i,int[] nums) {
int start = i;
int right = nums.length - 1;
while (start < right) {
swap(start,right,nums);
start++;
right--;
}
}
}