蓝桥杯训练day1
前缀和+差分
- 1.前缀和
-
- (1)3956. 截断数组
- (2)795. 前缀和
- (3)796. 子矩阵的和
- (4)1230. K倍区间
- (5)99. 激光炸弹
- 2.差分
-
- (1)797. 差分
- (2)差分矩阵
- (3)3729. 改变数组元素
- (4)100. 增减序列
1.前缀和
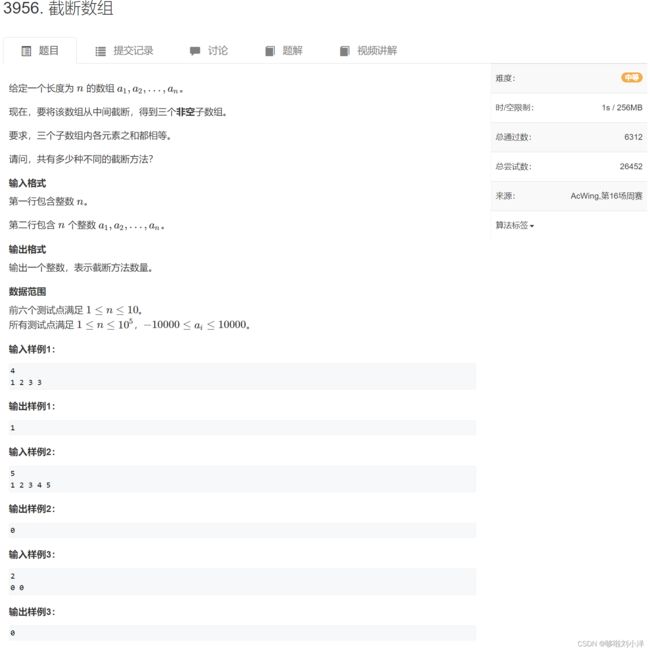
(1)3956. 截断数组
方法1:暴力
先用两个数组分别保存前缀和,后缀和。然后使用贪心思想来枚举后缀和的下标。
只有后缀和满足1/3的下标大于前缀和的下标,就加(具体看代码)过(19/22)数据
#include方法2:动态规划
枚举第二部分的位置,然后找第一部分有多少分割方案。使用动态规划的技巧来减少计算
#include(2)795. 前缀和
前缀和最简单的题目,模板题
用一个数组来记录前i个元素的和.
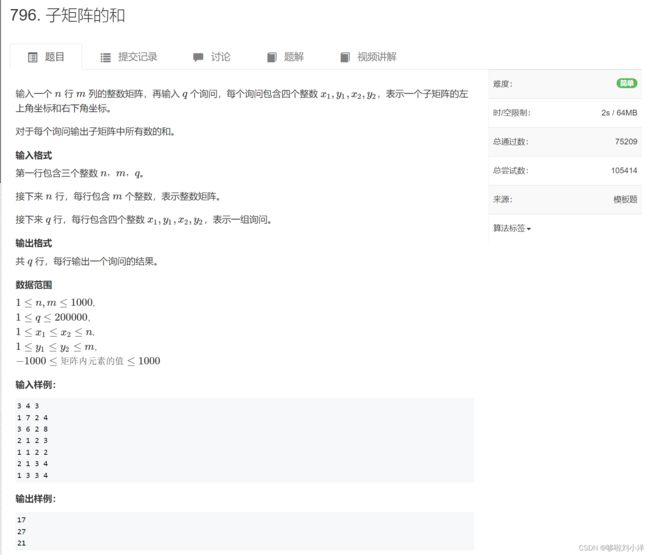
#include(3)796. 子矩阵的和
二维前缀和,
模拟过程,然后优化,反复几次即可掌握
#include(4)1230. K倍区间
这个题目,看的第一感觉应该是个简单题,没想到是个中等题,暴力只能过一半数据。
暴力:
#include想到
pre[r]-pre[l-1]=k
pre[r[=pre[l-1]+k
用pre[r]作为key,r作为key存储到哈希表,没想到也只多过一个数据
#include看了题解,发现距离答案一步之遥。在于
pre[r]-pre[l-1]=k等价于 pre[r]%k=pre[l-1]%k
所以找到两个前缀和相同的就好了,再利用一点动态规划的技巧.
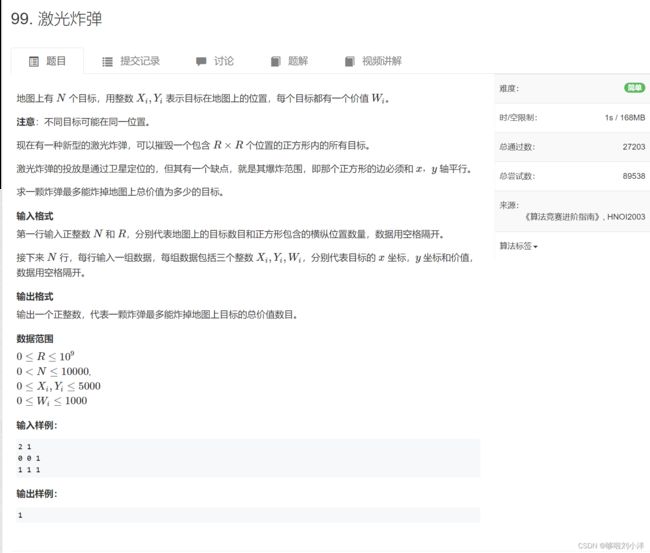
#include(5)99. 激光炸弹
#include2.差分
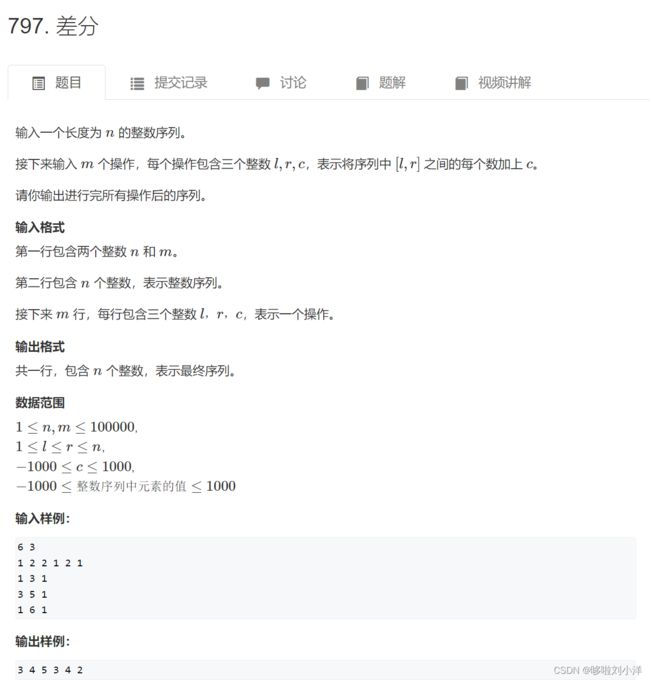
(1)797. 差分
#include(2)差分矩阵
同二维前缀和一样,就是扩展一个维度(但是很难哦)
#include(3)3729. 改变数组元素
说实话,这个题目放在差分下面,完全不知道和差分有什么关系。
就从后往前读一遍看看哪些位置可以为1就可以了,应该是个简单到不能再简单的题,,,
#include(4)100. 增减序列

这个题目难啊,由于所有的数都要一样,所有差分数组必须除了第一个数其余全是0.由于差分数组每次操作都需要b[L]+1,b[R+1]-1或b[L]-1,b[R+1]+1.所以将正数和负数相互抵消后,剩下的数要么和b[1]抵消,要么和b[n+1]抵消。
#include