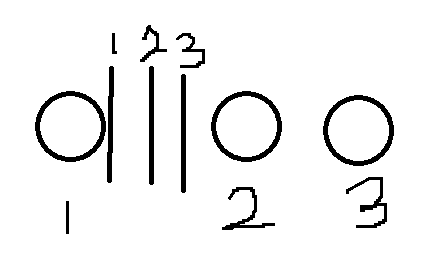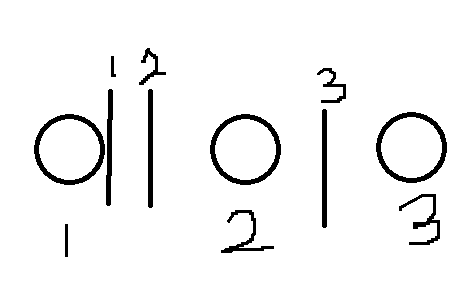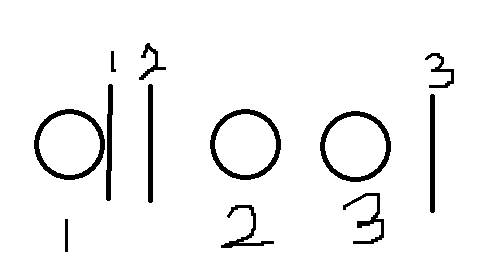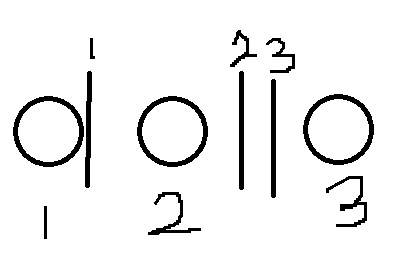2017.10.6 BJOI2015 bzoj4338 糖果
题目背景:
bzoj4338
分析:组合数
呜呜呜,为什么你们都推的出组合数······
本废喵死都没有推出组合数······
所以我们来详细考虑下这道题目:
首先,我们可以知道,如果我们求出填写一行的方式一共有t种,那么显然的,最后的答案就应该是P(t, n)即,t! / (t – n)!,所以我们要求取t,先把原题进行转化,
现在我们有k个珠子,然后有m个相同隔板,每一个隔板都放在某一个珠子的后面(一个珠子后面可以有多个隔板),一共有多少种不同的放法?
现在证明这两个问题为什么等价,我们可以发现,对于每一种放置的方法,都存在一个长度为m的序列a,a[i]表示第i个隔板前面是第几个珠子,隔板的顺序按其前面的珠子的编号来排
举个例子:当k = 3, m = 3时
case 1:
代表方案:1 1 1
case 2:
代表方案:1 1 2
case 3:
代表方案:1 1 3
case 4:
代表方案:1 2 2
case 5:
代表方案:1 2 3
case 6:
代表方案:1 3 3
case 7:
代表方案:2 2 2
case 8:
代表方案:2 2 3
case 9:
代表方案:2 3 3
case 10:
代表方案:3 3 3
一共10种方案,和10种图像一一对应,转化成立。
现在,我们得到了一个更加像组合数的题目,但是现在好像依然不好做,然后这一发我们再来转化一个题
我们有m + k个珠子,然后有m个隔板,每一个隔板可以放在编号2 ~ m + k的一个珠子后面,每个珠子后面只能够有一个隔板。
再来证明一下这个问题和上一个等价,现在因为我们保证了每个珠子后面只会有一个隔板,那么很显然的每两个隔板之间,必定有大于等于一个珠子,然后我们删去,每个隔板前面的那一个珠子,剩下的就是k个珠子和m个隔板,也就对应了上面一个转化问题的一种方案,也就应该对应了原题的一种方案,这个自己手动画图思考一下就好,我就只举两个例子了,
对应原题方案1 2 3
对应原题方案2 3 3
然后为什么只放2 ~ m + k后面呢,因为不然的话,放在以后面,删掉这个隔板前面的1,第一个隔板前面就没有东西了······
所以,我们相当于在 m + k - 1个位置中,选择出m个,所以最后获得的结论就是 t = C(m + k – 1, m)
有一种大功告成的喜悦····
感觉上,我们如果预处理一下阶乘和阶乘逆元,我们就可以得到60分了,是不是很开心,60分就是一个组合数取模,(然后本废喵什么都不知道,好了我们来解决最后的一步,组合数对合数取模,首先听说有个什么扩展lucas···本人表示我不懂····这个题,完全有更加暴力简单的做法,考虑,暴力分解因式,暴力分解出1 ~ m当中每一个质因数的有多少次方,直接先预处理1 ~ m当中的质数,然后暴力nloglogn 暴力枚举每一个质数的倍数然后除下去就好,然后因为我们知道,组合数肯定不可能出现分数,那么我们可以暴力在m + k - 1 ~ k当中除下来,因为我们知道小于等于a的最大的b的倍数,一定是 a - a % b 那么我们就可以找到每一个质数小于m + k - 1的第一个倍数,然后枚举后面的倍数把这个质数在1 ~ m中的次方除下去即可,最后暴力相乘取模就好了,好了,终于完结啦,撒花······(如果有不清楚的地方,参见代码
Update:
前段时间某dalao去请教了一下数竞dalao,发现了一种更好解释这个组合数的方法我们相当于在一个长度为m的数组当中填1 ~ k当中的一个数,然后,要单调不减,即数组a长度为m,对于i(i >= 1&& i <= m) a[i] >= a[i - 1], 然后定义b[i] = i + a[i],然后我们可以发先b[i] 严格大于 b[i - 1](i > i – 1, a[i] >= a[i - 1])然后考虑b[i] 的取值范围,因为第一个数,一定大于等于2,最大的数小于等于m + k,所以可以取的数位2 ~ m + k, 共有m + k - 1种选择,选择m个的方案数为C(m + k - 1, m)
Source:
/*
created by scarlyw
*/
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
inline char read() {
static const int IN_LEN = 1024 * 1024;
static char buf[IN_LEN], *s, *t;
if (s == t) {
t = (s = buf) + fread(buf, 1, IN_LEN, stdin);
if (s == t) return -1;
}
return *s++;
}
///*
template
inline void R(T &x) {
static char c;
static bool iosig;
for (c = read(), iosig = false; !isdigit(c); c = read()) {
if (c == -1) return ;
if (c == '-') iosig = true;
}
for (x = 0; isdigit(c); c = read())
x = ((x << 2) + x << 1) + (c ^ '0');
if (iosig) x = -x;
}
//*/
const int OUT_LEN = 1024 * 1024;
char obuf[OUT_LEN], *oh = obuf;
inline void write_char(char c) {
if (oh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), oh = obuf;
*oh++ = c;
}
template
inline void W(T x) {
static int buf[30], cnt;
if (x == 0) write_char('0');
else {
if (x < 0) write_char('-'), x = -x;
for (cnt = 0; x; x /= 10) buf[++cnt] = x % 10 + 48;
while (cnt) write_char(buf[cnt--]);
}
}
inline void flush() {
fwrite(obuf, 1, oh - obuf, stdout);
}
/*
template
inline void R(T &x) {
static char c;
static bool iosig;
for (c = getchar(), iosig = false; !isdigit(c); c = getchar())
if (c == '-') iosig = true;
for (x = 0; isdigit(c); c = getchar())
x = ((x << 2) + x << 1) + (c ^ '0');
if (iosig) x = -x;
}
//*/
const int MAXN = 100000 + 10;
long long n, m, k, mod, prime_cnt;
long long up[MAXN], down[MAXN], c[MAXN], prime[MAXN];
bool not_prime[MAXN];
inline void seive() {
not_prime[1] = true;
for (int i = 2; i < MAXN; ++i) {
if (!not_prime[i]) prime[++prime_cnt] = i;
for (int j = 1; j <= prime_cnt && prime[j] * i < MAXN; ++j) {
not_prime[i * prime[j]] = true;
if (i % prime[j] == 0) break ;
}
}
}
int main() {
R(n), R(m), R(k), R(mod), seive();
for (long long i = 1; i <= m; ++i) down[i] = i, up[i] = m + k - i;
for (long long i = 1; i <= prime_cnt; ++i) {
long long x = prime[i], cnt = 0;
for (long long j = x; j <= m; j += x)
while (down[j] % x == 0) cnt++, down[j] /= x;
c[i] = cnt;
}
for (long long i = 1; i <= prime_cnt; ++i) {
long long x = prime[i], s = m + k - 1LL- (m + k - 1LL) % x;
for (long long j = m + k - s; j <= m; j += x) {
while (c[i] && up[j] % x == 0) up[j] /= x, c[i]--;
if (c[i] == 0) break ;
}
}
long long sum = 1, ans = 1;
for (long long i = 1; i <= m; ++i) sum = sum * up[i] % mod;
for (long long i = 0; i < n; ++i) ans = ans * (long long)(sum - i) % mod;
std::cout << ans;
return 0;
}