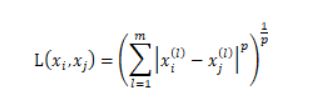机器学习--K近邻算法（KNN）（2）

一、简介

K-Nearest-Neighbor 算法是一种常用的监督学习算法，它没有显式的训练过程，是‘懒惰学习’的显著代表，此类学习算法仅在训练阶段将训练集保存起来，训练时间开销为0，待收到测试样本后在进行处理

k近邻模型的三要素： K值选择、距离度量、分类评价规则

二、工作机制

给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个‘邻居’的信息来进行预测。

在分类任务中，可使用“投票法”，即选择这k个样本中出现类别最多的标记作为预测结果；评价分类问题可以使用准确率 score

在回归任务中使用“平均法”，将这k个样本的实值输出标记的平均值作为预测结果；评价回归问题可以使用MSE（均方误差）、MAE（平均绝对值误差），需要注意，语法上y值必须是可以计算的数值类型。
最佳拟合：经验误差和泛化误差相近，泛化误差尽可能小

还可以基于距离远近进行加权平均或加权投票，距离越近，权重越大

距离度量方式：

其中p=2，就是欧氏距离
p=1，就是曼哈顿距离

三、算法实现

K近邻算法的实现最简单的方法是线性扫描，该方法要计算待预测样本与每一个训练实例的距离，当训练集很大时，计算非常耗时，显然这种方法不太可行。故引入kd树

如果实例点是随机分布的，kd树更适用于训练样本数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时。它的效率会迅速下降，几乎接近线性扫描。

3.1 KD树

Kd-树是K-dimension tree的缩写，是对数据点在k维空间（如二维(x，y)，三维(x，y，z)，k维(x1，y，z…)）中划分的一种数据结构，主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。本质上说，Kd-树就是一种平衡二叉树。

构造KD树相当于不断用垂直于坐标轴的超平面将K维空间进行切分，构成一系列的K维超矩形区域，直至子区域没有节点。KD树中的每一个节点对应于一个k维超矩形区域。

通常选择训练实例点再选定坐标轴上的中位数为切分点，这样得到平衡KD树，但平衡KD树不一定就是搜索效率最优的。

3.2 KD树搜索过程

①、在kd树中找出包含目标点的x的叶结点：从根结点出发，递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点。直到子结点为叶结点为止。
②、以此叶结点为“当前最近点”。
③、递归地向上回退，在每个结点进行以下操作：
（a）如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”。
（b）当前最近点一定存在于该节点的一个子结点对应的区域。检查该子结点的父结点的另一子结点对应的区域是否有更近的点。具体地，检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前最近点的距离为半径的超球体相交。如果相交，可能在另一个子结点对应的区域内存在距离目标点更近的点，移动到另一个子结点。接着，递归地进行最近邻搜索；如果不相交，向上回退。
④、当回退到根结点是，搜索结束，最后的“当前最近点”即为x的最近邻点。

四、简单应用

一般用于小样本集的数据模型，K不能为样本集的容量，K值不能为偶数。K的（经验）取值上限为sqrt（样本容量）

3.1 自定义数据集进行KNN预测（分类）

film:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# 导入我们自己构建的伪数据集
film = pd.read_excel('C:/Users/Administrator/Desktop/films.xlsx')

# 获取特征向量集合，和标签集合
y = film['类别'].copy()
X = film[['动作镜头','爱情镜头']].copy()

# 生成一组待预测样本
X_test = np.array([[11,6],[5,17]])

# 取X中的数值
X.values


# 绘制样本集在特征空间中的分布状况
plt.figure(figsize=(8,5))
plt.scatter(X['动作镜头'],X['爱情镜头'],s=100,c=y.map({
    '动作':0,
    '爱情':1
}),cmap=plt.cm.winter)
plt.legend([])

# 显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 给空间样本点添加图例描述，因为散点图不支持在绘图时添加图例
action = X.loc[y=='动作']
love = X.loc[y=='爱情']
s = 100
plt.scatter(action['动作镜头'],action['爱情镜头'],s=s,c='blue',label='动作电影')
plt.scatter(love['动作镜头'],love['爱情镜头'],s=s,c='cyan',label='爱情电影')
plt.xlabel('动作镜头')
plt.ylabel('爱情镜头')
plt.legend()

# 绘制测试点散点图
plt.scatter(X_test[:,0],X_test[:,1],s=100,marker='*',color='black')

# 导入 分类模型
from sklearn.neighbors import KNeighborsClassifier

# step1:构建算法对象
clf = KNeighborsClassifier(n_neighbors=3)

# step2: 训练算法对象 目的得到模型，模型有预测能力（本质为一个参数已知的函数）

# 注意：
# X 特征向量集合，必须为二维数组 VSM向量空间模型
# y 标签集合，一般为一维数组，也可能为多维数组
clf.fit(X,y)

# fit 之后clf分类器可以用来预测新数据

# step3：预测数据
clf.predict(X_test)

# 绘制第一二个点
p1 = plt.scatter(X_test[0,0],X_test[0,1],s=100,marker='*',c='blue')
p1 = plt.scatter(X_test[1,0],X_test[1,1],s=100,marker='*',c='cyan')

3.2 使用鸢尾花数据集进行KNN练习（分类）

绘制边界图像：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from sklearn import datasets

# 导入鸢尾花数据集
iris = datasets.load_iris()
# 特征向量集合
X = iris.data
# 标签集合
y = iris.target
# 字段名
feature_names = iris.feature_names
# 标签说明
target_names = iris.target_names

# 绘制样本数据的分布情况(绘制二维空间)，只取数据集的前两列研究
for i in range(target_names.size):
    condition = y ==i
    plt.scatter(X[condition][:,0],X[condition][:,1],label=target_names[i])
plt.legend()
plt.show()

# 以鸢尾花的前两列数据作为特征值， 标签作为标签
X = X[:,0:2]
y = y

# 生成鸢尾花训练集分布区间的所有点，作为测试数据
xmin, xmax = X[:,0].min()-0.05, X[:,0].max()+0.05
ymin, ymax = X[:,1].min()-0.05, X[:,1].max()+0.05

x_data = np.linspace(xmin, xmax, 100)
y_data = np.linspace(ymin, ymax, 100)

aa,bb = np.meshgrid(x_data,y_data)

X_test = np.concatenate((aa.reshape(-1,1),bb.reshape(-1,1)),axis=1)

# 绘制测试数据的图像
plt.scatter(X_test[:,0],X_test[:,1])

# 创建k值为3的KNN分类器对象
from sklearn.neighbors import KNeighborsClassifier
knn_3 = KNeighborsClassifier(n_neighbors=3)
knn_3.fit(X,y)
y_3 = knn_3.predict(X_test)

# 创建k值为10的KNN分类器对象
knn_10 = KNeighborsClassifier(n_neighbors=10)
knn_10.fit(X,y)
y_10 = knn_10.predict(X_test)

# 创建k值为样本容量的分类器对象
k = X.shape[0]
knn_all = KNeighborsClassifier(n_neighbors=k)
knn_all.fit(X,y)
y_all = knn_all.predict(X_test)

创建k值为经验上限的KNN分类器对象
k_max = int(np.sqrt(X.shape[0]))+1
knn_max = KNeighborsClassifier(n_neighbors=k_max)
knn_max.fit(X,y)
y_max = knn_max.predict(X_test)

# 封装绘制决策边界的函数
def show_edge(y_,k):
    plt.scatter(X_test[:,0],X_test[:,1],c=y_)
    for i in range(target_names.size):
        condition = y ==i
        plt.scatter(X[condition][:,0],X[condition][:,1],label=target_names[i])
    plt.legend()
    plt.title(label='k={}'.format(k))
    plt.show()

# 绘制图像
show_edge(y_3,3)      
show_edge(y_10,10)  
show_edge(y_max,k_max)  
show_edge(y_all,k)

结果展示：

样本数据分布情况：

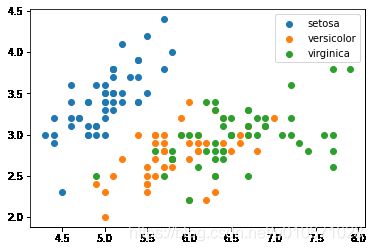
测试数据分布情况：

K=3,决策边界图像：

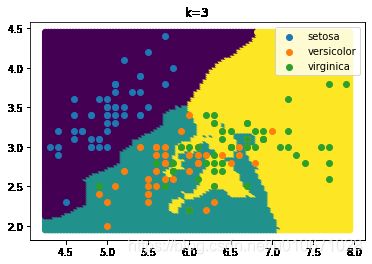
K=10,决策边界图像：

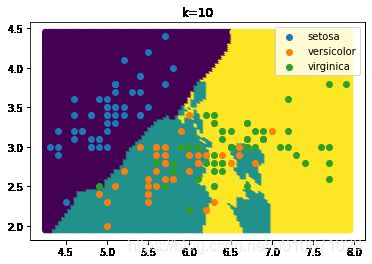
K=经验上限，即13,决策边界图像：

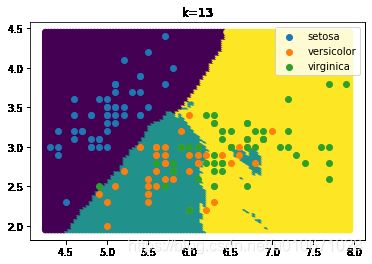
K=样本容量,决策边界图像：

使用样本数据评价上述模型

这样得到的准确率较高，一般不采用，通常进行拆分数据集
sklearn中的Classifier对象都有一个score方法，
score方法：对X中数据进行预测，并计算准确率

knn_3.score(X,y)
knn_10.score(X,y)
knn_max.score(X,y)
knn_all.score(X,y)

采用拆分数据集，来优化模型

按比例 37 28 19
大部分数据为训练数据 X_train,y_train 小部分数据为测试数据X_test,y_test

拆分原则：
随机拆分
保证样本均衡

# 将每一类数据前40个作为训练数据，后10个为测试数据
X_train_list = []
X_test_list = []
y_train_list=[]
y_test_list=[]
split=40
for i in range(3):
    condition = y==i
    X_c = X[condition]
    y_c = y[condition]
    X_train_list.append(X_c[:split])
    X_test_list.append(X_c[split:])
    y_train_list.append(y_c[:split])
    y_test_list.append(y_c[split:])
    
X_train = np.concatenate(X_train_list)
X_test = np.concatenate(X_test_list)
y_train = np.concatenate(y_train_list)
y_test = np.concatenate(y_test_list)

# 构造算法对象
knn1 = KNeighborsClassifier(n_neighbors=3)
knn2 = KNeighborsClassifier(n_neighbors=7)
knn3 = KNeighborsClassifier(n_neighbors=11)

# 训练
knn1.fit(X_train,y_train)
knn2.fit(X_train,y_train)
knn3.fit(X_train,y_train)

# 进行准确率评价
knn1.score(X_test,y_test)
knn2.score(X_test,y_test)
knn3.score(X_test,y_test)

寻找最优K

# 生成k值数组
k_list = np.arange(1,13,2)

# 封装调参的函数
def get_best_k(k_list):
    score_list=[]
    for k in k_list:
        knn = KNeighborsClassifier(n_neighbors=k)
        knn.fit(X_train,y_train)
        score_list.append(knn.score(X_test,y_test))
    return np.array(score_list)

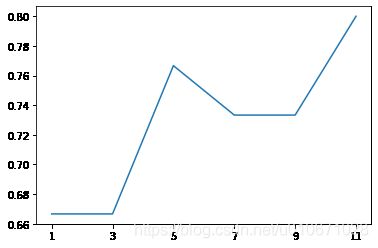
# 绘制k值对应准确率的折线图
plt.plot(k_list,get_best_k(k_list))
plt.xticks(k_list)

由此得出K=11，准确率最高，模型最优。

3.3 手写数字识别（分类）

了解sklearn 手写数字数据包 load_digits()：

key	values
feature_names	特征向量，64列
images	图像数据，shape=（1797，8，8）
target_names	标签名字
target	标签
data	扁平化处理后的图像数据，shape=（1797，64）

处理图形

图像处理一定要把图像进行扁平处理

图像必须灰度处理

灰度处理方法：
①、聚合：
plt.imshow(audi.mean(axis=2),cmap=‘gray’)

②、加权
plt.imshow(np.dot(audi,np.array([0.3,0.5,0.2])),cmap=‘gray’)

使用KNN分类模型预测手写数字数据集的

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
%matplotlib inline

# 手写数字的数据包
from sklearn.datasets import load_digits

# 保存原图形的形状
image_shape = image[0].shape

# 扁平处理
train = image.reshape(1797,-1)

# 获取数据标签
y = digits.target

# 封装一个拆分函数。sklearn也提供了此函数
def random_split(train,y,test_size,shuffle=False,random_state=None):
    
    if random_state != None:
        np.random.seed(random_state)
    if shuffle:
        shuffle_index = np.random.permutation(y.size)
        train = train[shuffle_index]
        y = y[shuffle_index]
    split = int(y.size*test_size)
    X_train = train[split:]
    X_test = train[:split]
    y_train = y[split:]
    y_test = y[:split]
     
    return X_train,X_test,y_train,y_test


# 求一个模型的评分序列
def knn_score(knn,count):
    scores = []
    for i in range(count):
        X_train,X_test,y_train,y_test = random_split(train,y,test_size=0.2,random_state=i)
        knn.fit(X_train,y_train)
        scores.append(knn.score(X_test,y_test))
    return np.array(scores)

# 比较不同的KNN模型的评分
def show_results(k_list,count):
    score_mean = []
    score_std = []
    for k in k_list:
        knn = KNeighborsClassifier(n_neighbors=k)
        scores = knn_score(knn,count)
        score_mean.append(scores.mean())
        score_std.append(scores.std())
    return pd.DataFrame({
        'K':k_list,
        'mean':score_mean,
        'std':score_std
    })

# 获取k值序列
max_k = int(np.sqrt(X_train.shape[0]))
k_list = np.arange(3,max_k,step=4)

# 调用函数
result = show_results(k_list,10)

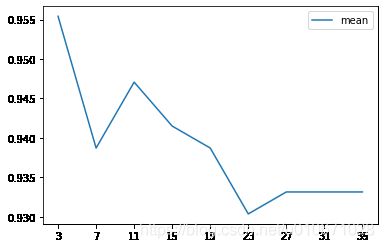
# 绘制效果图
plt.plot(result['K'],result['mean'],label='mean')
plt.legend()
plt.xticks(result['K'])
plt.show()

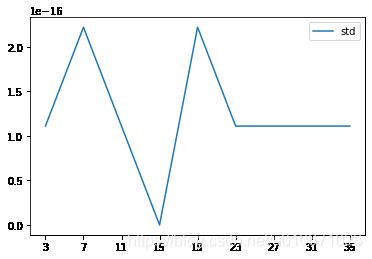
plt.plot(result['K'],result['std'],label='std')
plt.legend()
plt.xticks(result['K'])
plt.show()

绘图展示：


抽100个数据，使用最优模型进行预测结果展示：

# 取出样本集的特征向量集合和标签集合
data = digits.data
target = digits.target

# 由上图知道K=3为最优模型
best_model = KNeighborsClassifier(n_neighbors=3)
best_model.fit(data, target)
best_model.score(data, target)    # 0.993322203672788

# 取100个特征向量和标签
temp_data = data[:100]
temp_target = target[:100]

# 取100个预测值
y_ = best_model.predict(data)
temp_y_ = y_[:100]

# 绘制100张图像，观察其结果
sns.set_style(style='dark')
plt.figure(figsize=(18,22))
plt.title('RESULT')

for i in range(100):
    num_data = temp_data[i]
    num_y = temp_target[i]
    num_y_ = temp_y_[i]
    plt.subplot(10,10,i+1)
    title_color = 'blue'
    if num_y != num_y_:
        title_color = 'red'
    plt.title("T:{},P:{}".format(num_y, num_y_), color=title_color)
    plt.imshow(num_data.reshape(image_shape))

3.4 自定义数据集进行KNN回归问题的计算

KNN回归问题：语法上y值必须是可以计算的数值类型

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# 构造平米数x和房价y数据集
x = np.random.random(60)*60 + 60
f = lambda x:3*x + 2
bias = bias*np.array([1,-1])[np.random.randint(0,2,size=60)]
y = f(x) + bias

# 使用二维图像来表示房价与平米的关系，不是特征空间
sns.set()
plt.scatter(x,y)
plt.xlabel('m2')
plt.ylabel('RMB')

# 构造KNN回归模型
knn = KNeighborsRegressor(n_neighbors=5)

# 特征向量的vsm转换
X = x.reshape(-1,1)
knn.fit(X,y)
# 获取测试数据
X_test = np.linspace(X.max(),X.min(),100).reshape(-1,1)
y_ = knn.predict(X_test)

# 绘制图像
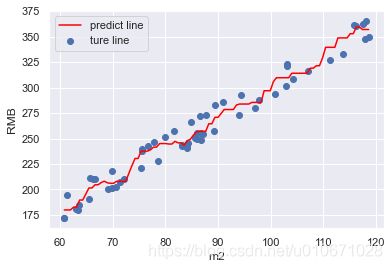
plt.plot(X_test,y_,label='predict line',color='red')
plt.scatter(x,y,label='ture line')
plt.xlabel('m2')
plt.ylabel('RMB')
plt.legend()

图像展示：

3.5 波士顿房价模型评价

from sklearn.datasets import load_boston
boston = load_boston()
data = boston.data
target = boston.target

# 获取经验上限k值
max_k = int(np.sqrt(X_train.size))

# 生成k值序列
k_list = np.arange(1,max_k,step=4)

# 封装评价KNN模型的函数
def mse_score(y,y_):
    return ((y-y_)**2).mean()


mse_train_list = []
mse_test_list = []
final_train_mse = []
final_test_mse = []
count = 10
# 循环k值序列
for k in k_list:
    knn = KNeighborsRegressor(n_neighbors=k)
    # 拆分count次样本集
    for i in range(count):
        X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=0.2,random_state=i)
        knn.fit(X_train,y_train)
    
        # 经验误差
        y_ = knn.predict(X_train)
        mse_train = mse_score(y_train,y_)
        mse_train_list.append(mse_train)
        # 泛华误差
        mse_test = mse_score(y_test,knn.predict(X_test))
        mse_test_list.append(mse_test)
    mse_train_list_mean = np.array(mse_train_list).mean()
    mse_test_list_mean = np.array(mse_test_list).mean()
    final_train_mse.append(mse_train_list_mean)
    final_test_mse.append(mse_test_list_mean)
    
result = pd.DataFrame({
    'K':k_list,
    'train_list':final_train_mse,
    'test_list':final_test_mse
})

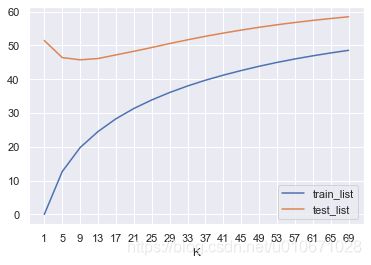
# 绘制图像
result.set_index('K').plot()
plt.xticks(k_list)
plt.show()

图像展示