使用DQN进行价格管理

---

前言

供应链和价格管理是企业运营中最早采用数据科学和组合优化方法的领域，并且在使用这些技术方面有着悠久的历史，并取得了巨大的成功。虽然有广泛的传统优化方法可用于库存和价格管理应用，但深度强化学习定价有潜力大幅提高这些和其他类型的企业运营的优化能力。

本次博客中，我将会和大家一起探讨强化学习在价格管理中的应用，分享内容主要分三部分

1. 首先我会通过一个简单的例子来说明传统价格优化问题的解法，以及优化的复杂性
2. 接着我会定义一个简单的价格管理环境，开发强化学习Optimizer，并评估其在价格管理 or 收益管理场景中的效果
3. 总结与展望，以及简单介绍另一篇进阶版强化学习在天猫动态定价中的应用

---

一、不同的价格响应

零售或制造业环境中的传统价格优化过程通常是使用某种需求模型对不同定价场景进行假设分析。在许多情况下，需求模型的开发具有挑战性，因为它必须正确地捕获影响需求的广泛因素和变量，包括常规价格、折扣、营销活动、季节性、竞争对手的价格、跨产品蚕食和光环效应。

然而，一旦建立了需求模型，定价决策的优化过程就相对简单了，线性或整数规划等标准技术通常就足够了。
例如，某生鲜电商在夏季季节开始时采购了一种季节性产品：西瓜，且必须在季节结束时将其销售一空。假如运营从离散集合中选择价格$[1,2,..,98,99]$，并且可以进行频繁的变价，我们可以提出以下的优化问题：
$$\begin{gathered} \max \sum _t\sum _j{p}_j\cdot d(t,j)\cdot x_{tj} \\ subjectto\sum _j{x}_{tj}=1,forallt \\ \sum _t\sum _{j}d(t,j)\cdot x_{tj}=c \\ {x}_{tj}\in 0,1 \end{gathered}$$

其中$t$代表时间间隔内迭代的时间戳，$j$代表有效价格水平上的索引，$p_j$代表索引为$j$的价格，$d(t,j)$代表在时间$t$给定价格索引$j$情况下的需求，$c$代表季节初的库存水平，并且$x_{tj}$是一个二进制的虚拟变量，如果价格索引被分配给时间间隔t那么$x_{tj}$就等于1，否则为0。第一个约束确保每个时间间隔只有一个有效价格，第二个约束确保总需求等于可用库存水平，这是个整数规划问题，可以用传统的优化lib来求解。

上面的模型【公式】非常灵活，因为它允许任意形状(线性、恒定弹性等)的价格需求函数和任意季节模式。它还可以直接扩展，以支持多个产品的联合价格优化。然而，上述模型假设时间间隔之间没有依赖关系。

我们在一些价格优化问题论文中[Online Network Revenue Management Using Thompson Sampling、Dynamic Learning and Pricing with Model Misspecification]往往会发现，论文通常假设价格需求响应函数是个简单的线性函数。然而在生鲜电商业务场景中，价格需求函数往往是非线性关系，同时，需求不仅取决于绝对价格水平，还可能受到近期价格变化幅度的影响——价格下降可能造成暂时的需求上涨，而价格上涨可能导致暂时的需求下降。价格变化的影响也可能是不对称的，因此价格上涨的影响比价格下跌的影响大得多或小得多。我们可以使用以下价格-需求函数对这些假设进行编码:
$$d(p_t,p_{t-1})=q_0-k\cdot p_t-a\cdot s((p_t-p_{t-1}{)}^{+})+b\cdot s((p_t-p_{t-1}{)}^{-})$$

其中

$$\begin{gathered} x^{+}=xifx>0,and0otherwise \\ {x}^{-}=xifx<0,and0otherwise \end{gathered}$$

$p_t$是当前时间间隔内的价格，$p_{t-1}$是前一个时间间隔内的价格，公式的前两部分代表一个截距$q_0$，斜率$k$的线性需求模型。后两项模拟了在两个时间间隔内的价格变化的响应。参数$a$，$b$分别代表价格上涨、下跌的敏感度。$s$是一个冲击函数，可以用来指定价格和需求变化之间的非线性关系，在本demo中，我们用$s(x)=\sqrt{x}$。

为了可视化方便，我们先定义并实现一些可视化函数：

import math 
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('seaborn-white')
import pandas as pd
from matplotlib import animation, rc
plt.rcParams.update({'pdf.fonttype': 'truetype'})

from qbstyles import mpl_style
mpl_style(dark=False)

# Visualization functions

from bokeh.io import show, output_notebook
from bokeh.palettes import PuBu4
from bokeh.plotting import figure
from bokeh.models import Label

output_notebook()

def plot_return_trace(returns, smoothing_window=10, range_std=2):
    plt.figure(figsize=(16, 5))
    plt.xlabel("Episode")
    plt.ylabel("Return ($)")
    returns_df = pd.Series(returns)
    ma = returns_df.rolling(window=smoothing_window).mean()
    mstd = returns_df.rolling(window=smoothing_window).std()
    plt.plot(ma, c = 'blue', alpha = 1.00, linewidth = 1)
    plt.fill_between(mstd.index, ma-range_std*mstd, ma+range_std*mstd, color='blue', alpha=0.2)

def plot_price_schedules(p_trace, sampling_ratio, last_highlights, fig_number=None):
    plt.figure(fig_number);
    plt.xlabel("Time step");
    plt.ylabel("Price ($)");
    plt.xticks(range(T))
    plt.plot(range(T), np.array(p_trace[0:-1:sampling_ratio]).T, c = 'k', alpha = 0.05)
    return plt.plot(range(T), np.array(p_trace[-(last_highlights+1):-1]).T, c = 'red', alpha = 0.5, linewidth=2)

def bullet_graph(data, labels=None, bar_label=None, axis_label=None,
                size=(5, 3), palette=None, bar_color="black", label_color="gray"):
    stack_data = np.stack(data[:,2])

    cum_stack_data = np.cumsum(stack_data, axis=1)
    h = np.max(cum_stack_data) / 20

    fig, axarr = plt.subplots(len(data), figsize=size, sharex=True)

    for idx, item in enumerate(data):

        if len(data) > 1:
            ax = axarr[idx]

        ax.set_aspect('equal')
        ax.set_yticklabels([item[0]])
        ax.set_yticks([1])
        ax.spines['bottom'].set_visible(False)
        ax.spines['top'].set_visible(False)
        ax.spines['right'].set_visible(False)
        ax.spines['left'].set_visible(False)

        prev_limit = 0
        for idx2, lim in enumerate(cum_stack_data[idx]):
            ax.barh([1], lim - prev_limit, left=prev_limit, height=h, color=palette[idx2])
            prev_limit = lim
        rects = ax.patches
        ax.barh([1], item[1], height=(h / 3), color=bar_color)

    if labels is not None:
        for rect, label in zip(rects, labels):
            height = rect.get_height()
            ax.text(
                rect.get_x() + rect.get_width() / 2,
                -height * .4,
                label,
                ha='center',
                va='bottom',
                color=label_color)
            
    if bar_label is not None:
        rect = rects[0]
        height = rect.get_height()
        ax.text(
            rect.get_x() + rect.get_width(),
            -height * .1,
            bar_label,
            ha='center',
            va='bottom',
            color='white')
    if axis_label:
        ax.set_xlabel(axis_label)
    fig.subplots_adjust(hspace=0)

接下来，我们研究一下上述价格响应函数的最优价格计划是什么样子的。我们首先实现计算给定价格表(几个时间步骤的价格向量)的利润的函数:

## 仿真
def plus(x):
    return 0 if x < 0 else x

def minus(x):
    return 0 if x > 0 else -x

def shock(x):
    return np.sqrt(x)

# 价格需求响应函数
def q_t(p_t, p_t_1, q_0, k, a, b):
    return plus(q_0 - k*p_t - a*shock(plus(p_t - p_t_1)) + b*shock(minus(p_t - p_t_1)))

# 在t时刻的利润
def profit_t(p_t, p_t_1, q_0, k, a, b, unit_cost):
    return q_t(p_t, p_t_1, q_0, k, a, b)*(p_t - unit_cost) 

# 在len(p)个时间间隔中，实时价格向量p所获得的总利润
def profit_total(p, unit_cost, q_0, k, a, b):
    return profit_t(p[0], p[0], q_0, k, 0, 0, unit_cost) + sum(map(lambda t: profit_t(p[t], p[t-1], q_0, k, a, b, unit_cost), range(1, len(p))))

# 在len(p)个时间间隔中，实时价格向量p所获得的需求向量
def demand_total(p,a,b):
    return q_t(p[0], p[0], q_0, k, 0, 0) + sum(map(lambda t: q_t(p[t], p[t-1], q_0, k, a, b), range(1,len(p))))

我们从某业务场景中sample一些数据来进行分析，在实际场景中，西瓜采购成本在不同的采购批次价格是不同的，demo中为了简化，使用历史一段时间内的平均价格作为采购成本30元，价格集合：$[1,2,...,98,99]$，其中假如我们是每7天进行一次变价，那么在西瓜整个销售周期中，我们可以进行19次定价：

## 参数
T = 19
price_max = 100
price_step = 1
q_0 = 1000
k = 20
unit_cost = 30
a_q = 50
b_q = 150

## 参数简化
def profit_t_response(p_t, p_t_1):
    return profit_t(p_t, p_t_1, q_0, k, a_q, b_q, unit_cost)

def profit_response(p):
    return profit_total(p, unit_cost, q_0, k, a_q, b_q)

## 可视化价格需求函数
price_grid = np.arange(price_step, price_max, price_step)
price_change_grid = np.arange(0.5, 1.5, 0.05)
profit_map = np.zeros( (len(price_grid), len(price_change_grid)) )
for i in range(len(price_grid)):
    for j in range(len(price_change_grid)):
        profit_map[i,j] = profit_t_response(price_grid[i], price_grid[i]*price_change_grid[j])

plt.figure(figsize=(20, 8))
for i in range(len(price_change_grid)):
    if math.isclose(price_change_grid[i], 1.0):
        color = 'black'
    else:
        p_norm = (price_change_grid[i]-0.5)/1
        color = (p_norm, 0.4, 1 - p_norm)
    plt.plot(price_grid, profit_map[:, i], c=color)
plt.xlabel("Price ($)")
plt.ylabel("Profit")
plt.legend(np.int_(np.round((1-price_change_grid)*100)), loc='lower right', title="Price change (%)", fancybox=False, framealpha=0.6)
plt.grid(True)

如上图所示，黑色那条曲线是基准利润曲线【价格不变】，当我们将商品降价后，曲线开始膨胀【颜色越来越红】，总利润 or 总收益 上扬；当我们将商品涨价后，曲线开始收缩【颜色越来越蓝】，30元为商品成本，价格为30元处，总利润或总收益为0
接下来我们使用基本的优化方法来构建本demo的两条基线。

• 最优不变价格
• 使用顺序贪心搜索法（one by one）来获得最优价格调度

# 最优不变价格
profits = np.array([ profit_response(np.repeat(p, T)) for p in price_grid ])
p_idx = np.argmax(profits)
price_opt_const = price_grid[p_idx]

print(f'最优价格为 {price_opt_const}, 获得的最大利润为 {profits[p_idx]}')

最优价格为 40, 获得的最大利润为 38000.0

结合上面的曲线图及我们计算出的结果，我们在T个时间步中采用恒定价格的方式在这种环境下【需求不仅取决于绝对价格水平，还可能受到近期价格变化幅度的影响】不是最优的。因此我们可以通过贪婪优化来提高利润：首先在第一个时间步骤中找到最优价格，然后在固定第一个时间步骤的情况下优化第二个时间步骤，依此类推:

# 最优价格序列
def find_optimal_price_t(p_baseline, price_grid, t):
    p_grid = np.tile(p_baseline, (len(price_grid), 1))
    p_grid[:, t] = price_grid
    profit_grid = np.array([ profit_response(p) for p in p_grid ])
    return price_grid[ np.argmax(profit_grid) ]

p_opt = np.repeat(price_opt_const, T)
for t in range(T):
    price_t = find_optimal_price_t(p_opt, price_grid, t)
    p_opt[t] = price_t

print(p_opt)
print(f'获得的最佳利润为 is {profit_response(p_opt)}')

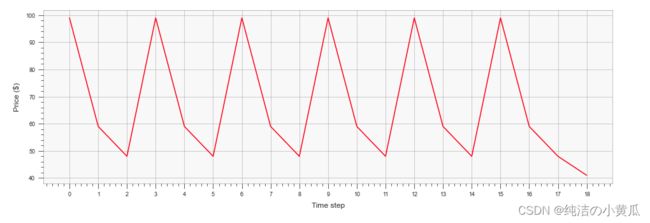
plt.figure(figsize=(16, 5))
plt.xlabel("Time step")
plt.ylabel("Price ($)")
plt.xticks(np.arange(T))
plt.plot(np.arange(T), p_opt, c='red')

[99 59 48 99 59 48 99 59 48 99 59 48 99 59 48 99 59 48 41]
获得的最佳利润为 is 198145.7051278035

由上图可知，由于价格-需求函数内部的一个简单的时间依赖性决定了一个复杂的价格策略，包括价格上涨和折扣促销。
零售通常有两种定价策略，一种是基于促销的Hi-Lo的定价策略，另一种是稳定定价的EDLP策略。中国电商平台和多数业态目前是Hi-Lo的定价策略，刺激消费者到店或者刺激消费者流量。它可以被视为许多零售商、电商使用的Hi-Lo定价策略有效性的一个证明;
从上图我们看到改变常规价格和促销价格可以最大化商品利润。上面的例子也说明了价格管理和强化学习优化之间的关系。我们所定义的价格响应函数本质上是一个微分方程，其中利润不仅取决于当前的价格行为，还取决于价格的动态。可以预期，这种方程可以表现出非常复杂的行为，特别是在长时间间隔内，因此相应的控制策略也可以变得复杂。因此，这种策略的优化需要强大而灵活的方法，例如深度强化学习。

二、利用DQN优化定价策略

尽管我们上面实现的贪心算法为一个简单的微分价格响应函数生成了最优定价计划，但当我们添加更多的约束或相互依赖时，用线性或整数规划来求解就变得越来越具有挑战性。在这次demo中，我们从不同的角度来解决这个问题，并应用一个通用的深度Q网络(DQN)算法来学习最优价格控制策略。
我们在这个例子中使用原始的DQN，因为它是一个相当简单的起点，说明了现代强化学习的主要概念。在实际设置中，可能会使用原始DQN的最新修改或替代算法，RLib中也有更加鲁棒的开源算法可供参考。

1.定义环境

强化学习考虑的是一个智能体以离散时间步长与环境交互的设置，其目标是学习奖励最大化的行为策略。在每个时间步$t$，在给定状态$s$，代理根据策略$\pi (s)$执行操作$a$，同时获得了奖励$r$，并进入了下一个状态$s^{{}^{\prime }}$。
我们在强化学习中重新定义了我们的价格环境：首先，我们在任何时间步$t$对环境状态进行编码，$s_t$作为之前所有时间步长的价格向量，并与时间步本身的one-hot编码相连接:
$$s_t=(p_{t-1},p_{t-2},...,p_0,0,...)|(0,...,1,...,0)$$
接下来， 每个时间步长内的动作$a$只是有效价格水平数组中的一个索引。最后是奖励$r$就是卖家的利润。我们的目标是找到一种基于当前状态规定定价行为的策略，以使销售季的总利润最大化。

2.DQN算法概述

在这里我们简要回顾下最原始的DQN算法

DQN算法的目标是在$T$的时间步长中，学习一个动作策略$\pi$，该策略能够最大化累计奖励总额（也被称为回报）：
$$R=\sum _{t=0}^T{\gamma }^t{r}_t$$

我们定义一个函数$Q$，它可以根据当前状态和下一个操作来估计预期收益，假设所有后续操作也将根据该策略执行:
$$Q^{\pi }(s,a)={\mathbb{E}}_{s,a}[R]$$

假如这个函数（称为$Q$函数）是已知的，策略$\pi$可以简单定义如下，以实现收益最大化：
$$\pi (s)=\underset{a}{\mathrm{argmax}}Q(s,a)$$

我们可以将上面的定义组合成以下的递归方程：
$$Q^{\pi }(s,a)=r+\gamma \underset{a^{{}^{\prime }}}{\max }Q(s^{{}^{\prime }},a^{{}^{\prime }})$$

其中$s^{{}^{\prime }}$，$a^{{}^{\prime }}$是下一个状态，以及在那种状态下采取的行动。如果我们使用近似函数来估计Q函数，那么可以通过这个方程两边的差值来近似度量这个近似函数的质量。

$$\delta =Q^{\pi }(s,a)-(r+\gamma \underset{a^{{}^{\prime }}}{\max }Q(s^{{}^{\prime }},a^{{}^{\prime }}))$$

这个值$\delta$称为时间差分误差，DQN背后的主要思想是训练一个深度神经网络，使用时间差分误差作为损失函数来近似$Q$函数。
原则上，训练过程可以很简单:

1. 初始化网络。它的输入对应于状态表征，而输出是所有动作的$Q$值向量。
2. 对每个时间步：
   1. 使用网络估计$Q$值
   2. 执行$Q$值最大的action，并观察奖励reward
   3. 计算误差$\delta$
   4. 使用随机梯度下降法更新网络参数，损失函数是由时间差误差推导出来的。

然而，这种简单的方法对于训练复杂的非线性逼近器(如深度神经网络)是不稳定的。DQN使用两种技术解决这个问题:

• Replay buffer：上面描述的基本训练过程的一个问题是，序列化的观测对象通常是相关的，但是网络训练一般需要独立分布的样本。
  DQN通过累计多个观察到的转换$(s,a,r,s^{{}^{\prime }})$进入缓存，然后对这样的转换进行批量抽样以重新训练网络。缓存通常要足够大，以最小化样本之间的相关性。

• Target networks：基本过程的第二个问题是，网络参数是根据使用同一网络产生的$Q$值计算的损失函数更新的。换句话说，学习目标与我们试图学习的参数同时移动，使得优化过程不稳定。DQN通过维护两个网络实例缓解了这个问题。第一个实例用来执行操作，并按照上面描述的方法不断更新。第二个被称为目标网络，是第一个网络的滞后副本，专门用于计算损失函数(即目标)的$Q$值。这种技巧有助于稳定学习过程。将基本学习过程与这两种思想相结合，得到DQN算法。

3.Algorithm: Deep Q Network (DQN)

1. 参数及初始化
   1. $\varphi$ – 策略网络$Q_{\varphi }$的参数
   2. ${\varphi }_{targ}$ – 目标网络$Q_{{\varphi }_{targ}}$
   3. $\alpha$ – 学习率
   4. $N$ – batch size
   5. $T_u$ – 目标更新频率
   6. 初始化${\varphi }_{targ}=\varphi$
2. For $t=1,...,MAX\_STEPS$ do

   1. 基于$Q_{\varphi }(s_t,a_t)$选择action(价格)

   2. 执行该操作并保存转换$(s_t,a_t,r_t,s_t^{{}^{\prime }})$进缓存

   3. 更新策略网络

      1. 从buffer中抽样batch size为N的转换
      2. 计算batch中每个样本的目标$Q$值

      $$y_i=r_i+\gamma \underset{a^{{}^{\prime }}}{\max }{Q}_{{\varphi }_{targ}(s^{{}^{\prime }},a^{{}^{\prime }})}$$
      其中，$Q(s,a)=0$是整个过程的最近状态（初始条件）

      3. 计算loss：
         $$L(\varphi )=\frac{1}{N}\sum _i(y_i-Q_{\varphi }(s_i,a_i){)}^2$$
      4. 更新网络参数：
         $$\varphi =\varphi -\alpha {\nabla }_{\varphi }L(\varphi )$$

   4. $ift\mathrm{mod}{T}_u=0then$

      1. 更新目标网络：${\varphi }_{targ}\leftarrow \varphi$

我们需要解决的最后一个问题是如何根据网络估计的$Q$值选择动作action。
从Thompson Sampling那篇paper中，我们知道总是以最大$Q$值采取行动action的策略不会很好地work，因为学习过程不会充分地探索环境，因此我们选择随机化选择过程，来提高模型的exploration的能力。
更具体地说，$\epsilon$-greedy策略以 $1-\epsilon$ 的概率选择最大Q值对应的action，其中随机化action的概率为 $\epsilon$

同时我们还使用退火技术，从一个相对较大的 $\epsilon$ 值开始，随着训练阶段，逐步减少 $\epsilon$ 大小。

# 第三方库
import math
import random
import numpy as np
from IPython.display import clear_output
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple
from itertools import count
import torch.nn.functional as F

import torch
import torch.nn as nn
import torch.optim as optim

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

使用Pytorch实现DQN

第一步是实现一个内存缓冲区，用于保存观察到的转换，并在网络训练期间重现它们:

Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))

class ReplayMemory(object):                             
    def __init__(self, capacity):
        self.capacity = capacity
        self.memory = []
        self.position = 0

    def push(self, *args):                                     # push new transition to the buffer
        if len(self.memory) < self.capacity:
            self.memory.append(None)
        self.memory[self.position] = Transition(*args)
        self.position = (self.position + 1) % self.capacity    # cyclic buffer

    def sample(self, batch_size):                              # sample transitions from the buffer 
        return random.sample(self.memory, batch_size)
    
    def __len__(self):
        return len(self.memory)

第二步是实现策略网络。网路的输入是环境状态，输出是每个可能定价行为的$Q$值向量。我们选择实现一个具有三个完全连接层的简单网络，尽管循环神经网络(RNN)在这里也是一个合理的选择，因为状态本质上是一个时间序列:

class PolicyNetworkDQN(nn.Module):
    def __init__(self, state_size, action_size, hidden_size=128):
        super(PolicyNetworkDQN, self).__init__()
        layers = [
              nn.Linear(state_size, hidden_size),
              nn.ReLU(),
              nn.Linear(hidden_size, hidden_size),
              nn.ReLU(),
              nn.Linear(hidden_size, hidden_size),
              nn.ReLU(),
              nn.Linear(hidden_size, action_size)
        ]
        self.model = nn.Sequential(*layers)

    def forward(self, x):
        q_values = self.model(x)
        return q_values  

接下来，我们定义将网络产生的$Q$值转换为定价行为的策略。我们使用带退火机制的$\epsilon$-greedy策略来搜索参数：采取随机行动的概率 $\epsilon$
在训练过程开始时设置得相对较高，然后以指数级衰减来微调策略。

class AnnealedEpsGreedyPolicy(object):
    def __init__(self, eps_start = 0.9, eps_end = 0.05, eps_decay = 400):
        self.eps_start = eps_start
        self.eps_end = eps_end
        self.eps_decay = eps_decay
        self.steps_done = 0

    def select_action(self, q_values):
        sample = random.random()
        eps_threshold = self.eps_end + (self.eps_start - self.eps_end) * math.exp(-1. * self.steps_done / self.eps_decay)
        self.steps_done += 1
        if sample > eps_threshold:
            return np.argmax(q_values)
        else:
            return random.randrange(len(q_values))

实现中最复杂的部分是网络更新过程。它从缓冲区中采样一批非最终动作action，计算当前和下一个状态的q值，计算损失，并相应地更新网络:

GAMMA = 1.00
TARGET_UPDATE = 20
BATCH_SIZE = 512

def update_model(memory, policy_net, target_net):
    if len(memory) < BATCH_SIZE:
        return
    transitions = memory.sample(BATCH_SIZE)
    batch = Transition(*zip(*transitions))

    non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)), device=device, dtype=torch.bool)
    non_final_next_states = torch.stack([s for s in batch.next_state if s is not None])

    state_batch = torch.stack(batch.state)
    action_batch = torch.cat(batch.action)
    reward_batch = torch.stack(batch.reward)

    state_action_values = policy_net(state_batch).gather(1, action_batch)

    next_state_values = torch.zeros(BATCH_SIZE, device=device)
    next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()

    # Compute the expected Q values
    expected_state_action_values = reward_batch[:, 0] + (GAMMA * next_state_values)  

    # Compute Huber loss
    loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
    
    # Optimize the model
    optimizer.zero_grad()
    loss.backward()
    for param in policy_net.parameters():
        param.grad.data.clamp_(-1, 1)
    optimizer.step()

最后，我们定义了一个helper函数，它执行动作并返回奖励和更新状态

def env_intial_state():
    return np.repeat(0, 2*T)

def env_step(t, state, action):
    next_state = np.repeat(0, len(state))
    next_state[0] = price_grid[action]
    next_state[1:T] = state[0:T-1]
    next_state[T+t] = 1
    reward = profit_t_response(next_state[0], next_state[1])
    return next_state, reward

def to_tensor(x):
    return torch.from_numpy(np.array(x).astype(np.float32))

def to_tensor_long(x):
    return torch.tensor([[x]], device=device, dtype=torch.long)

DQN训练

policy_net = PolicyNetworkDQN(2*T, len(price_grid)).to(device)
target_net = PolicyNetworkDQN(2*T, len(price_grid)).to(device)
optimizer = optim.AdamW(policy_net.parameters(), lr = 0.005)
policy = AnnealedEpsGreedyPolicy()
memory = ReplayMemory(10000)

target_net.load_state_dict(policy_net.state_dict())
target_net.eval()

num_episodes = 1800
return_trace = []
p_trace = [] # price schedules used in each episode
for i_episode in range(num_episodes):
    state = env_intial_state()
    reward_trace = []
    p = []
    for t in range(T):
        # 选择并执行action
        with torch.no_grad():
            q_values = policy_net(to_tensor(state))

        action = policy.select_action(q_values.detach().numpy())
        
        next_state, reward = env_step(t, state, action)

        # 将转换存在缓存中
        memory.push(to_tensor(state), 
                    to_tensor_long(action), 
                    to_tensor(next_state) if t != T - 1 else None, 
                    to_tensor([reward]))

        # 移动到下一个状态
        state = next_state

        # 更新模型
        update_model(memory, policy_net, target_net)

        reward_trace.append(reward)
        p.append(price_grid[action])

    return_trace.append(sum(reward_trace))
    p_trace.append(p)

    # 更新目标网络，并拷贝网络参数
    if i_episode % TARGET_UPDATE == 0:
        target_net.load_state_dict(policy_net.state_dict())

        clear_output(wait = True)
        print(f'Episode {i_episode} of {num_episodes} ({i_episode/num_episodes*100:.2f}%)')

plot_return_trace(return_trace)

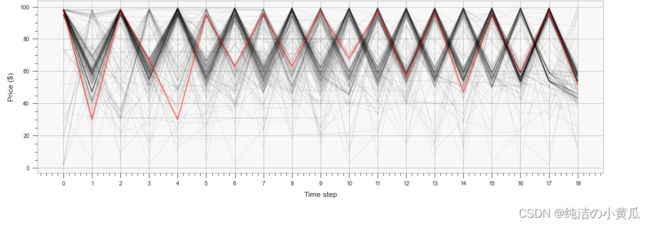
fig = plt.figure(figsize=(16, 5))
plot_price_schedules(p_trace, 5, 1, fig.number)

for profit in sorted(profit_response(s) for s in p_trace)[-10:]:
    print(f'Best profit results: {profit}')

实验及结果分析

plt.ioff()
fig = plt.figure(figsize=(16, 5))
def animate(t):
    fig.clear()
    plot_price_schedules(p_trace[0:t], 5, 1, fig.number)

ani = matplotlib.animation.FuncAnimation(fig, animate, frames=range(10, 1000, 10), interval=50, blit=False, repeat_delay=500)
ani.save('sim.gif', dpi=80, writer='pillow', fps=20)
rc('animation', html='jshtml')

# Visualize Q values for a given state
sample_state = [40.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0., \
                1.,     0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.]
Q_s = policy_net(to_tensor(sample_state))
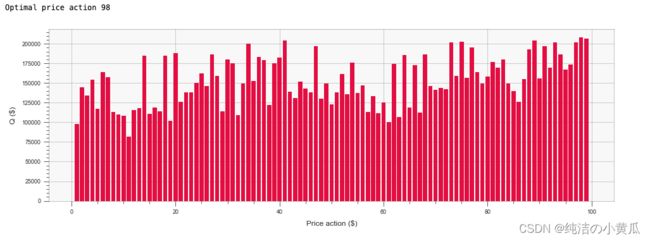
a_opt = Q_s.max(0)[1].detach()
print(f'Optimal price action {price_grid[a_opt]}')

plt.figure(figsize=(16, 5))
plt.xlabel("Price action ($)")
plt.ylabel("Q ($)")
plt.bar(price_grid, Q_s.detach().numpy(), color='crimson',  width=0.8, alpha=1)
plt.show()

---

总结

强化学习-定价、决策

• 强化学习的技术框架：model-free vs model-based
  • 一种方法就是Model-based方法，让agent学习一种模型，这种模型能够从它的观察角度描述环境是如何工作的，然后利用这个模型做出动作规划;但是，事实证明，我们有时候并不需要对环境进行建模也能找到最优的策略，一种经典的例子就是Q-learning，Q-learning直接对未来的回报进行估计，表示对状态下执行动作后获得的未来收益总和的估计，这些方法由于没有去对环境进行建模，因此他们都是Model-free的方法
• 强化学习vs传统优化方法、机器学习模型：
  • 传统价格优化，主要聚焦于量价关系函数的估计及单点价格优化，强化学习可以在序列化价格或库存变动优化中发力。
  • 传统的模型被训练用作优化点击率、转化率等直接的指标，强化学习可以在一系列营销策略：变价、流量曝光、广告引流等操作下来实现最大化收益或长期价值。
• 强化学习落地方向：制造、物流、营销、游戏
  • 游戏、下围棋很成功（其环境都是已经给定的，那里面的所有规则都是非常清楚的，所以我们可以在计算机的环境里面进行大量的采样，那么我们可以取得达到人类专家、甚至是能够超越人类水平的效果）
• 强化学习在真实业务场景落地成功的关键：好的环境（真实业务中的环境都是一些真实、开放的、一些边界不那么确定的一些环境），人为设定模拟器来模拟环境（knowledge-driven）, 从数据上面还原模拟器（data-driven）
• 强化学习成功应用案例：【淘宝搜索、滴滴出租车、菜鸟仓库派单】
• 定价领域强技术路线：1.人来做决策；2.人为设定模拟器；3.用预测的方法来代替决策【无法寻优】；4.数据驱动的模拟器

参考论文及源码

1. Mnih V., et al. “Human-level control through deep reinforcement learning”, 2015 [原始DQN网络论文]
2. Hessel M., et al. “Rainbow: Combining Improvements in Deep Reinforcement Learning,” 2017 [DQN网络的优化及扩展]
3. https://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html [pytorch DQN 实现源码]
4. Ferreira K., Simchi-Levi D., and Wang H. – Online Network Revenue Management Using Thompson Sampling, November 2017 [基于汤普森抽样的动态定价模型，前分享论文]
5. Nambiar, Mila, David Simchi-Levi, and He Wang. “Dynamic learning and pricing with model misspecification.” Management Science 65.11 (2019): 4980-5000. [model misspecification下的动态定价，前分享论文]
6. Kemmer L., et al. “Reinforcement learning for supply chain optimization,” 2018 [利用强化学习实现供应链优化]
7. High–low pricing https://en.wikipedia.org/wiki/High%E2%80%93low_pricing [高低定价策略]
8. https://www.reddit.com/r/MachineLearning/comments/f2sd5s/r_deep_reinforcement_learning_for_supply_chain/ [reddit深度强化学习做供应链优化讨论]
9. Reinforcement Learning: An Introduction https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf [斯坦福强化学习基础介绍]
10. https://arxiv.org/abs/1912.02572 Dynamic Pricing on E-commerce Platform with Deep Reinforcement Learning: A Field Experiment [基于深度强化学习的电子商务平台动态定价]
11. Deep Reinforcement Learning for Supply Chain and Price Optimization