【机器学习】马尔可夫链与隐马尔可夫模型(HMM)

1.马尔可夫链(Markov Chain)

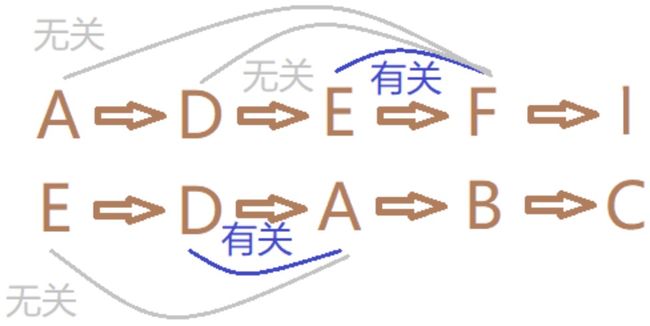
        马尔可夫链（Markov chain），又称离散时间马尔可夫链（discrete-time Markov chain），因俄国数学家安德烈·马尔可夫（A.A.Markov）得名。描述的是状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。马尔科夫链作为实际过程的统计模型具有许多应用。

        在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点，每一步可以移动到任何一个相邻的点，在这里移动到每一个点的概率都是相同的（无论之前漫步路径是如何的）

        举例说明1:

                一只被切除了大脑的白鼠被随机丢进如下洞穴, 小白鼠在洞穴间随机蹿动。

         窜动的路线就构成一个马尔科夫链。因为这只白鼠已没有了记忆，瞬间产生的念头决定了它从一个洞穴蹿到另一个洞穴；当其所在位置确定时，它下一步蹿往何处与它以往经过的路径无关。

         这种在已知“现在”的条件下，“未来”与“过去”彼此独立的特性就被称为马尔科夫性，具有这种性质的随机过程就叫做马尔科夫过程，其最原始的模型就是马尔科夫链。

  举例说明2:

        设定一个人有三种状态分布，分别是吃、睡、玩。假设他每个状态的转移都是有概率的。

        转移概率矩阵P，是保持不变的，就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。有了这个矩阵，再加上已知的第一天的状态分布，就可以计算出第N天的状态分布了。

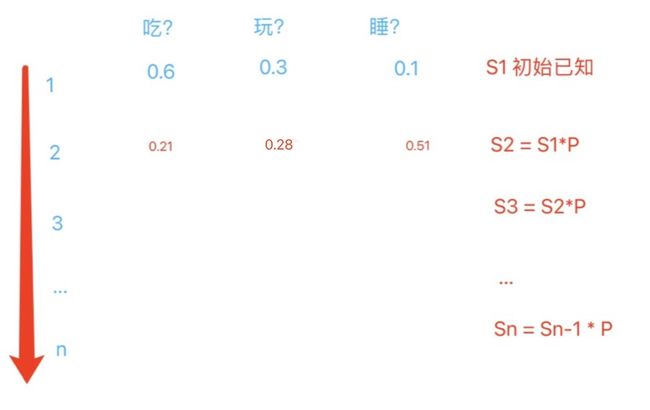
        S1 是4月1号中午12点的的状态分布矩阵 [0.6, 0.3, 0.1]，里面的数字分别代表吃的概率，玩的概率，睡的概率。

        4月2号的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。

        4月3号的状态分布矩阵 S3 = S2 * P (看见没，跟S1无关，只跟S2有关)。

        4月4号的状态分布矩阵 S4 = S3 * P (看见没，跟S1，S2无关，只跟S3有关)。

        4月n号的状态分布矩阵 Sn = Sn-1 * P (看见没，只跟它前面一个状态Sn-1有关)。

4月2号的状态分布矩阵计算过程：

2.隐马尔科夫模型（Hidden Markov Model，HMM）

        隐马尔科夫模型（Hidden Markov Model，HMM）是结构最简单的动态贝叶斯网络（dynamic bayesian network），也是一种有向图模型。隐马尔科夫模型相比马尔科夫链多了一个观测链 O，即马尔科夫链中每到一个状态，都会有一个观测输出。隐马尔科夫模型里面的“隐”字就是说有一种隐含状态，我们不能直接观测得到，而是根据另一种与之有关的可以直接观测到的可见状态去推算隐含状态最有可能的结果。

        假设观察者距离洞穴很远, 看不见老鼠窜动的轨迹, 但是每个洞穴中都装有不同颜色的灯, 当老鼠进入到该洞穴时会触发开关将灯点亮, 观察者可以看清被点亮的灯的颜色。

 假设老鼠窜动的轨迹如下

 那么观察者看到的灯亮的顺序则为

 一个隐马尔可夫模型则可以如下表示

 小白鼠在洞穴(状态)之间的转移存在转移概率, 可由矩阵表示:

        这个矩阵称为状态转移概率分布矩阵, 如小白鼠从房间F窜到房间C的概率为0.33

        假如实验中开关发生故障, 每次进入洞穴后点亮的灯的颜色不再确定, 而是每种颜色的灯亮存在概率, 如下矩阵:

        这个矩阵称为观测状态概率矩阵, 如小白鼠进到F洞穴, 红灯亮的概率为0.15, 绿灯亮的概率为0.7, 蓝灯亮的概率为0.15。

        小白鼠最初被随机丢进每个洞穴的初始概率为：

        隐马尔科夫模型由初始状态概率向量、状态转移概率矩阵和观测概率矩阵决定。和决定状态序列，决定观测序列。因此，隐马尔科夫模型λ可以由三元符号表示，即：。,,称为隐马尔科夫模型的三要素。

        隐马尔可夫模型中存在两个很重要的假设：

        （1）次马尔科夫链假设。即任意时刻的隐藏状态只依赖于它前一个隐藏状态。

        （2）观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态。

        隐马尔可夫模型属于有向图模型, 需要计算的概率是“观测序列(输入)和状态序列(输出)的联合概率”，即P(状态序列, 观测序列), 然后再根据贝叶斯公式求解出P(状态序列|观测序列), 构建它们的联合概率分布P(Y,X)的模型属于生成式模型

Reference:
        1.https://www.jianshu.com/p/667f5bb15367

        2.马尔可夫链 （Markov Chain）是什么鬼 - 知乎