【蓝桥杯】刷题日记,冲刺国赛
目录
1.递增三元组
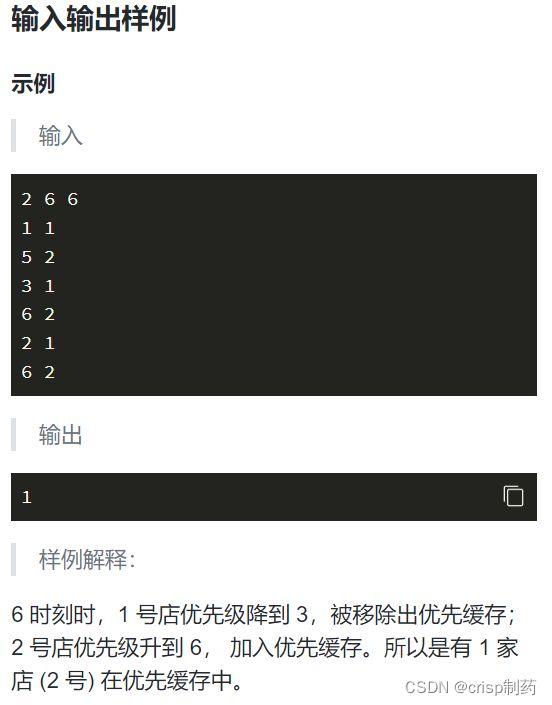
2.外卖优先级
3.最大乘积
5.含2天数
6.K倍区间
7.扫地机器人
8.数的幂次
9.机器人行走
10.天干地支
11.求值
1.递增三元组
解题思路:这题我们将运用到前缀和的思想,先记录a数组中比b【i】要小的数的个数,即为0-b【i-1】的前缀和,然后再找c数组中比b【i】要大的数的个数,统计个数,然后再用乘法原理就可以求出我们的答案
#include
using namespace std;
typedef long long LL;
const int N =100010;
int n;
int a[N],b[N],c[N];
int x[N],y[N];//x数组用于统计在a数组中比b【j】要小的数个数,y用于记录在c数组中比b【i】要大的数的个数
int cnt[N],s[N];//记录个数的数组,s是存前缀和的数组,前缀和是统计个数。
int main()
{
scanf("%d",&n);
//全部加一防止前缀和出现越界问题
for(int i=0;i 2.外卖优先级
题解思路:这题就是道比较复杂的模拟具体看代码吧
#include
#include
#include
using namespace std;
const int N=100010;
typedef pairPII;
PII a[N];//存时间和id
int score[N],last[N];//存店铺的优先级,最后的时间
bool st[N];//判断店铺是否进入优先缓存
int main()
{
int n,m,time;
scanf("%d%d%d",&n,&m,&time);
for(int i=0;i5)st[id]=true;//如果大于5就把该店铺放进优先缓存中。
last[id]=t;//更新一下最后时刻
}
for(int i=1;i<=n;i++)
if(last[i] 3.最大乘积
解题思路:暴力1-9的全排列,如何分成两个数字然后不断移动乘号就好
#include
#include
using namespace std;
bool pre(int num) {
int x = num;
int arr[10] = {0};
while (x != 0) //把这个数的每一位存进数组中
{
arr[x % 10]++;
x /= 10;
}
if(arr[0] != 0) return false;//判断是否含有0
for (int i = 1; i < 10; i++) //判断是否有重复的数字
if (arr[i] != 1)return false;
return true;
}
int main() {
int sum = 0;
int arr[9] = {1,2,3,4,5,6,7,8,9};
do {
int a = arr[8];
int b = arr[0];
for(int i = 1; i < 8; i++)
{
b *= 10;
b += arr[i]; //构建1~9这9个数字组成的数
}
int weight = 10;//可以看成权重
while (b != 0) {
if (pre(a * b) && a <=b) {
if (a*b > sum)
sum = a*b;
}
//下面是移动乘号的过程
a = (b % 10) * weight + a;
b /= 10;
weight *= 10;
}
}while (next_permutation(arr, arr + 9));
cout << sum;
return 0;
} 4.阶乘约数
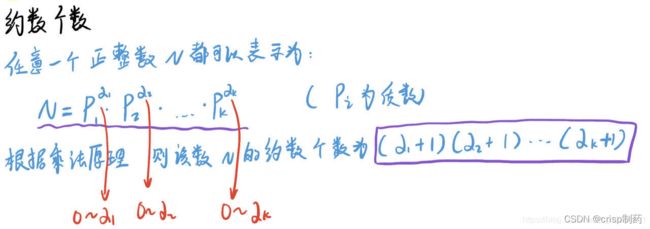
解题思路:这题用的是一个唯一分解定理
先求出1-100的全部的质数,然后再根据公式进行求解
#include
using namespace std;
int a[100];
int main()
{
for(int i=2;i<=100;i++)
{
int n=i;
for(int j=2;j<=n/j;j++)
{
while(n%j==0)
{
a[j]++;
n/=j;
}
}
if(n>1)
{
a[n]++;
}
}
long long ans=1;
for(int i=2;i<=100;i++)
{
if(a[i])
ans*=(a[i]+1);
}
cout< 5.含2天数
题解思路:暴力模拟,如果年份是含有2的话那就在判断是否为闰年是的话则有366天否则365天,如果年份中没有2的话,在判断一下是否为闰年,那一年有2的天数为31+120+29,否的话则天数为31+120+28,12月有31天,2月有28天,剩下的十个月每个月只有2,12,20~29一共12天带2所以一共有120天。
#include
using namespace std;
bool pd(int x)//判断是否含有2
{
while(x!=0)
{
if(x%10==2)return true;
x/=10;
}
return false;
}
bool run(int x)//判断是否为闰年
{
if(x%400==0||x%4==0&&x%100!=0)
{
return true;
}
return false;
}
int main()
{
int n=0,t=0;
for(int i=1900;i<=9999;i++)
{
if(pd(i))
{
if(run(i))
{
n=366;
}
else{
n=365;
}
}
else
{
if(run(i))
{
n=31+120+29;
}
else{
n=31+120+28;
}
}
t+=n;
}
cout< 6.K倍区间
解题思路:这题再次用到前缀和,以及取模运算的定理(a+b) % p = (a%p + b %p) %p
sum[r] % k 和 sum[l-1] % k 的余数如果相等,那么sum[r] - sum[l-1]的差值必然是k的倍数 ,比如说
13 % 7 和 20 % 7 (20-13)%7 =0;由这个例子可得两个前缀和相同的数可以组成一个k倍区间
#include
using namespace std;
const int N=100010;
typedef long long ll;
int sum[N],a[N],res[N];//ans是计算相同组合个数,res是用来统计不同前缀和的个数值
int n,k;
ll ans=0;
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=(sum[i-1]+a[i])%k;//前缀和取模
ans+=res[sum[i]];//更新答案
res[sum[i]]++;//两个相等的前缀和就能组成一个k倍区间
}
cout< 7.扫地机器人
题解思路
划定区间,该区间为每个机器人的活动的范围,检测该范围可不可以满足全部扫到
用二分搜索,检查时,给每一个区间划分范围 程序中用到的是 [l,l+m] (l左边界,m区间大小)
每次循环都更新l,并将l左边的范围全部清扫完,最后判断是否扫完,l>=n,如果花费t时间可以刚好完成,那么花费比t多的时间一定可以完成,比t少的时间一定不能完成
二分的判断是:
每个机器人优先处理他左边的,如果还有时间就处理他右边的
如果向右边处理,找到他右边的机器人,那么他右边的机器人一开始就向右处理一定更优
#include
#include
using namespace std;
const int N = 1e5 + 5;
int n, m;
int a[N];//机器人的位置
bool check(int x){
int l = 0;
for(int i = 0; i < m; i++){
if(a[i] - x <= l){//当前机器人扫描的最左范围小于等于上一个机器人的最右范围
if(a[i] <= l) l = a[i] + x - 1;// 若机器人 在左边界内 边界就该等于机器人向右所能扫到的最远点
else l += x;//如果当前位置大于边界的话那就+上x来到达机器人的位置
}else return false;//当前机器人扫的最左边都无法达到上一个机器人扫的最右边,二者中间有不能够扫的格子
}
if(l >= n) return true;//扫完了n个格子
else return false; // 遍历完机器人 若左边界小于 n 则说明没有全部清扫
}
int main(){
cin >> n >> m;//读入方格数和机器人数量
for(int i = 0; i < m; i++) cin >> a[i];//机器人的位置
sort(a, a + m);
int l = 0, r = n, mid= 0;
while(l < r){
mid = (l + r) >> 1;
if(check(mid)){//时间等于mid时全部扫了每一个格子,r = mid,在[l, r]内寻找更小的时间
r = mid;
}
else l = mid + 1;/*时间等于mid时没有扫完每一个格子,l = mid + 1,在[l, r]内寻找更大的时间来满足扫完每一个格子*/
}
cout << 2 * (l - 1) << endl;//花费时间=()区间大小-1)*2
return 0;
}
8.数的幂次
经典的快速幂模板题,直接看代码吧
#include
using namespace std;
long long qmi(long long a,int b,int p)
{
long long res=1;
while(b)//对b进行二进制化,从低位到高位
{
//如果b的二进制表示的第0位为1,则乘上当前的a
if(b&1) res = res *a %p;
//b右移一位
b>>=1;
//更新a,a依次为a^{2^0},a^{2^1},a^{2^2},....,a^{2^logb}
a=a*a%p;
}
return res;
}
int main()
{
int n;
scanf("%d", &n);
while (n -- )
{
int a, b, p;
scanf("%d%d%d", &a, &b, &p);
printf("%lld\n", qmi(a, b, p));
}
return 0;
} 9.机器人行走
#include
using namespace std;
typedef long long LL;
int main()
{
int n;
cin>>n;
while(n--)
{
double x=0,y=0;
string s;
cin>>s;
int t=0;//代表方向
for(int i=0;i<(int)s.size();i++)
{
if(s[i]=='R')//定义左右方向
{
t+=1;
t%=4;
}
else if(s[i]=='L')
{
t+=3;
t%=4;
}
else
{
int sum=s[i]-'0';//把字符串转换为数字
i++;
while(s[i]!='R'&&s[i]!='L'&&s[i]!='\0')
{
sum*=10;
sum+=s[i]-'0';
i++;
}
i-=1;
if(t==1)
{
x+=sum;
}
else if(t==2)
{
y-=sum;
}
else if(t==3)
{
x-=sum;
}
else{
y+=sum;
}
}
}
printf("%0.2lf\n",sqrt(x*x+y*y)*1.0);
}
return 0;
} 10.天干地支
这题直接暴力模拟
#include
using namespace std;
char a[10][10]={"geng","xin","ren","gui","jia","yi","bing","ding","wu","ji"};
char b[12][10]={"zi","chou","yin","mao","chen","si","wu","wei","shen","you","xu","hai"};
int main()
{
int n;
cin>>n;
if(n>=2020)
{int x=(n-2020)%10;
int y=(n-2020)%12;
printf("%s%s\n",a[x],b[y]);
}
else{
int x=(10-(2020-n)%10)%10;
int y=(12-(2020-n)%12)%12;
printf("%s%s\n",a[x],b[y]);
}
return 0;
} 11.求值
暴力模拟题
#include#include using namespace std; int main() { /* for(int i=100;;i++) 直接暴力,由于是填空题,防止超时直接输出答案即可 { int cnt=0; for(int j=1;j<=i;j++) { if(i%j==0) { cnt++; } } if(cnt==100) { cout<