从0开始的CNN学习之路(二)-新疆大学智能制造现代产业学院
目录
一、CNN的本质
二、损失函数 (Loss Function)
三、梯度下降
1.梯度下降
2.梯度爆炸
3.损失函数的局部最优解和全局最优解
4.BGD(批量梯度下降)
5.SGD(随机梯度下降)
6.mini-BGD(小批量梯度下降)
7.补充:
四、Logistic(逻辑斯蒂)回归
总结
前言
上一章我们通过RCNN算法,来给大家讲解了NMS,IOU等一些概念,让大家目标了RCNN在提取到特征后是如何进行目标检测的,那么从这一章,我将带大家一起分析,CNN是是如何利用提取的特征进行训练的
这一章,我们主要讲解损失函数和梯度下降,BP算法以及BN层卷积层等这些概念将在下一章讲解,大家不用担心
一、CNN的本质
首先,关于CNN,我认为它的本质就是一个数学模型:y=ax+b,只不过实际上这个模型要远远比y=ax+b复杂的多,其中的权重a和偏置b,就是我们要训练的网络模型
在CNN中,权重是指每个神经元连接的权值。对于卷积神经网络,权重主要包括卷积层和全连接层中的参数。
在卷积层中,权重通常由卷积核组成,每个卷积核都是一个小的矩阵,它在输入图像的不同位置执行卷积操作,从而提取图像的特征。每个卷积核的权重是在训练过程中学习得到的。
在全连接层中,权重是每个神经元连接的权重,这些权重决定了输入数据和输出数据之间的线性变换。每个神经元的权重也是在训练过程中学习得到的。
除了权重之外,卷积神经网络中还包括偏置(bias)参数,也就是上面提到的偏置b,偏置是在每个神经元上添加的一个常数,用于调整神经元的输出。偏置参数也是在训练过程中学习得到的。
理解了权重的含义后,那我们应该就能明白,我们训练神经网络的最终目的,就是得到合适的网络参数用来组成权重,这样只要我们将图片放入网络模型后使用合适的权重来训练,就能够得到正确的结果
所以,我们现在需要知道,如何才能够得到合适的网络参数,也就是如何训练出一个优秀的模型,因此,我们需要引入一个新的概念---损失函数(Loss Function)
二、损失函数 (Loss Function)
损失函数是用来计算模型的计算值与真实值之间距离的函数,换句话来说就是用来评判模型好坏的,如果损失函数的值越小,就说明模型计算值与真实值之间的距离越近,即模型越好
假设我们有下图一个模型:
那么该模型的损失函数如下图所示:
即检测值与真实值差的平方,这种损失函数叫做均方误差损失函数(MSE),实际上还有很多种损失函数,如L1损失函数,交叉熵损失函数等,大家下去可自行了解,不同的模型用不一样的损失函数,效果也是不一样的,在这里只是以MSE举例来帮助大家理解
注:最小二乘损失函数和MSE的区别在于,MSE需要除以样本总数m,而最小二乘则不需要
三、梯度下降
1.梯度下降
上文说到,我们使用损失函数可以知道训练模型的好坏,那么我们的目的是要一个好的模型,也就说,需要损失函数最小时的模型,因此我们现在的目标转换为使损失函数降低,找到损失函数的最优解
而找到损失函数最小时的最优解的方法,便是梯度下降
如上图所示公式,便是梯度下降的权重参数更新公式,其中α是学习率,θ是我们训练的模型参数,具体我们以下面这个例子来进行理解
如图是损失函数的函数图,当 θ在图上所示的点时,该点的梯度是整数,我们用θ值减去该点梯度,那么得到的新的θ值便会向左移,一直重复此操作,直到θ移动到谷底,也就是梯度为0的点时,θ将停止更新,而此点也就是损失函数的最低点,即最优解
2.梯度爆炸
在这里我们考虑一下α,即学习率,如果α的值过于大的话,那么将有一种可能:θ在进行第一次梯度更新时会越高最低点,移动到谷底左边,最终会来回左右震荡,并不断上升,直至内存不够系统报错
这种现象,就叫做梯度爆炸,为了避免这种结果,我们需要选择合适大小的学习率,既不能过大(会导致梯度爆炸),也不能过小(会导致梯度下降缓慢),因此学习率α是一个很敏感的值,我们可以通过不断尝试,选取合适的α值
同时,我们可以给不同的参数 θ选取不同的α值,代表不同参数的不等价
3.损失函数的局部最优解和全局最优解
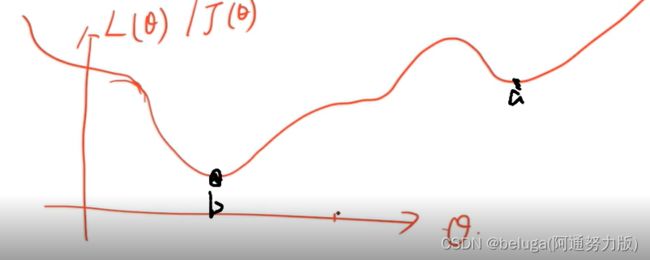
上文说过,我们通过梯度下降可以找到损失函数的最优解,但是如果 θ在a点附件,进行梯度下降的话,那么结果毫无疑问,它会落在a点,可是我们从图中可以看到,a点并不是损失函数的最小值,最小值应该是b点,对于这种情况,我们把a点称为损失函数的局部最优解,b点称为损失函数的全局最优解
4.BGD(批量梯度下降)
为了避免这种情况,我们引入了batch(批次)的概念,当batch等于全部样本时,即我们用数据集的所有数据来进行梯度下降,这样我们就可以避免陷入局部最优解的情况
但是,这种方法每迭代一步,都要用到训练集所有的数据,如果样本数目很大,那么可想而知这种方法的迭代速度将会非常缓慢!
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
5.SGD(随机梯度下降)
如果当batch等于一个样本时,这种方法叫做随机梯度下降,即每一次只随机取一个样本来进行梯度下降,这种方法增加了训练的随机性,但是是收敛性能不好,会导致结果在最优点附近晃动,并且仅以当前样本点进行最小值求解,通常无法达到真正局部最优解,但可以比较接近
优点:训练速度快,增加随机性并降低计算机要求,有时也可跳出局部最优解,但有可能又落入另一个局部最优解
缺点:准确度下降,并不是全局最优,并且走弯路,曲线会震荡,但总体是下降的
注:SGD虽然训练速度快,但是在样本量庞大时就显得收敛速度比较慢了,计算量非常庞大。此时BGD是要比SGD快的
6.mini-BGD(小批量梯度下降)
既然BGD和SGD各有优缺点,那么我们为什么不将其进行融合,采取一个折中的办法呢,于是,我们得到了mini-BGD(小批量梯度下降)
当batch是一个不为1的较小数时,我们将其称为小批量梯度下降
注:如显存够大,可调大batch,如果要增加随机性,则可以适当调小batch
7.补充:
1.严格意义上讲,只有当batch=1时,才能叫SGD,但现在基本上只要batch不等于全部数据集,都可以认为其是SGD(很多论文作者都是这么搞得)
2.BGD也是随机的,也可以认为是随机梯度下降
3.设数据集数量n=1000,batch size=10,那么我们训练一百次才能训练1个enpoch,即一轮
4.如果损失函数不是凸函数,BGD将无法取得全局最优解
四、Logistic(逻辑斯蒂)回归
逻辑回归是用来进行分类的,并不是回归,这点要注意
他的思想和上文说的梯度下降并无出入,在这里主要介绍一下他的损失函数
如何感兴趣,大家可以自行查找相关博客
上图为逻辑回归的模型和损失函数,这里可以看到逻辑回归使用的并不是上文我们提到过的MSE损失函数,而是交叉熵损失函数,这里是因为如果我们使用MSE得话,得到的将会是一个非凸函数,这样我们进行梯度下降的话,我们将无法得到最优解
因此,我们在这里要注意一点:如果能选择凸函数的话,我们要尽可能选择凸函数,而逻辑回归的损失函数就是一个很典型的凸函数
总结
以上就是今天要讲的内容,本文主要介绍了神经网络如何利用提取的特征来进行训练更新模型参数,当然这并不是全部内容,还有更重要的BP算法将在后面讲解,谢谢大家
(如果觉得文章可以,来个一键三连鼓励鼓励呗)