机器人空间采样算法研究现状简述

‍

[文末提供原文PDF免费下载(期刊论文版式)]‍

‍ 摘要：运动规划是移动机器人自主导航系统中的重要模块之一，相关算法研究成果层出不穷，本文将空间采样算法拆解为四个子类算法：PRM类算法、RRT类算法、CVM类算法和DWA类算法，并沿时间顺序概述相关算法的发展历程，最后从模型复杂度、实时性、环境适应能力及路径曲线质量等方面分析了上述四类算法的优缺点。

01 引言

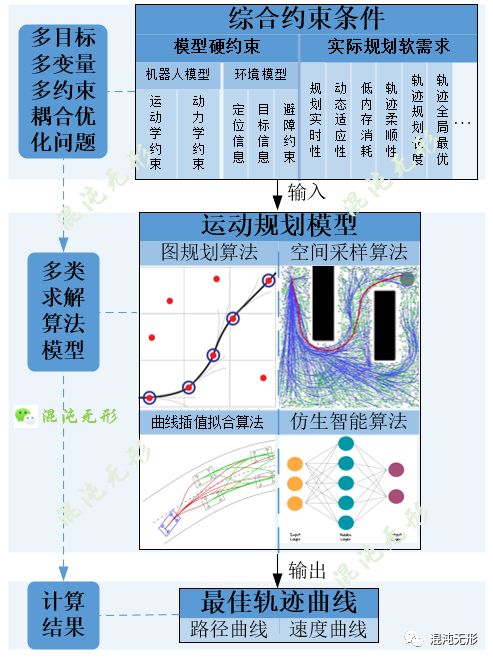
在前文《机器人图规划算法研究现状简述》中，结合图 1.1对“运动规划是什么？要解决什么问题？”这两个问题有详细阐述，并概述了运动规划与运动控制模型、环境感知这两个部分之间的关系。

图 1.1 运动规划示意图（图片来源：http://wiki.ros.org/navigation）

如图 1.2所示，运动规划的研究主要是对多目标多变量多约束耦合的规划模型优化求解。对于具有非完整约束的移动机器人而言（见《两轮差速驱动机器人运动模型及应用分析》），在分布有障碍物的环境中求解最优路径是NP-hard问题，即对于任意场景无法保证在多项式时间内求得最优解，因此大部分规划算法追求次优解或局部最优[1]。

诸多学者针对不同应用场景和需求，设计、改进了非常多的运动规划算法，其中常见的运动规划算法主要包括四类：图规划算法、空间采样算法、曲线插值拟合算法和仿生智能算法，通过规划模型求解得到最佳轨迹曲线，包含无碰撞顺滑的路径曲线和平滑的速度曲线，并输入到控制器驱动机器人运动。

本文将对空间采样算法领域的研究进展及成果进行分类阐述，主要概述同族算法的发展过程，不对具体算法展开分析，在后续系列文章会挑选部分经典常用算法深入剖析。

图 1.2 运动规划通用模型

02空间采样算法研究分析
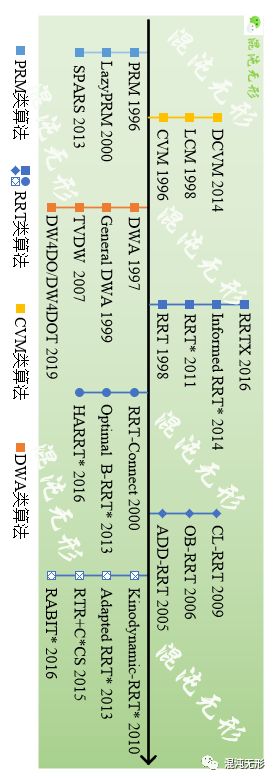
空间采样算法按照采样空间不同，可分为：状态空间采样和运动空间采样。如图 2.1所示，基于状态空间采样的算法能够在大面积、高纬度的空间中快速生成路径，包括RRT和PRM类算法等，具有概率完备性，其主要步骤包括随机采样、度量连接、碰撞检测和路径查询。基于运动空间采样的算法则在速度空间等距采样，通过评价函数选择最佳控制指令，驱动机器人运动，主要包括CVM类算法及DWA类算法等。

（请横屏看图）

图 2.1 空间采样算法发展路线概况

2.1PRM类算法

第一类算法是PRM（Probabilistic Road Map）类算法，此类算法的核心思想是：构建连通图，搜索最佳路径。

构建连通图：在C空间（Configuration Space）（对应图 2.2中的所有区域）中随机抽样，采集一系列点，并检测它们是否在自由空间（白色区域）中，并使用本地规划器尝试将这些采样点相互连接起来，仅保留与障碍物无交集的连线，结合起始点和目标点，得到一张连通图；搜索最佳路径：使用图搜索算法基于上述连通图搜索无碰撞路径。

图 2.2 PRM算法（图片来源：https://en.wikipedia.org/wiki/Probabilistic_roadmap）

结合图 2.1，传统PRM[2]算法基于环境模型构建路径网络图，并查询生成最佳路径，采样点数越多，计算结果越好。Bohlin等人在此基础上进一步拓展，如LazyPRM[3]通过减少调用局部规划器次数（减少不要的碰撞检测）以提升规划效率，SPARS2[4]构建稀疏、稠密双重图，进一步提高算法收敛速度，且渐进最优。

2.2RRT类算法

第二类算法是RRT（Rapidly Exploring Random Tree）类算法，此类算法的核心思想和PRM相似：RRT也是在搜索空间中随机采样，并以起始点或终止点为树根节点开始扩展，仅连接符合约束条件的临近采样节点，直到树中的某一节点靠近目标点或起始点，最后基于上述生成的树搜索出一条最短路径。

图 2.3 RRT算法（图片来源：https://github.com/AtsushiSakai/PythonRobotics）

所以，不同于PRM图状结构，RRT采用树状结构，查询效率更快。传统RRT[5]算法与传统A*算法在多方面极为相似，诸多研究者对传统RRT算法也做出相似的改进，本文根据RRT特性分为单向、双向、导向及非全向四种类型，具体如下：

• 单向搜索

Karaman、Gammell等人针对RRT随机性强、路径粗糙及动态适应性差等问题提出了改进算法，如RRT*[6]可重计算新节点实现渐进最优，Informed RRT*[7]基于初始路径采用椭圆收缩策略，减少锯齿状路径情况，RRTX[8]设计重规划策略以适应动态环境，提升算法的实用性。

图 2.4 Informed RRT*（图片来源：https://github.com/AtsushiSakai/PythonRobotics）

• 双向搜索

Kuffner、Jordan等人为提升搜索效率，同时从起点、终点构建两（多）棵树，如RRT-connect[9]，Optimal B-RRT*[10]在此基础上加入了启发式函数，进一步提高收敛速度，HARRT*[11]将同伦拓扑空间与双向树结合，并从理论上证明了该方法的有效性。

图 2.5 RRT-connect（图片来源：https://arxiv.org/pdf/1703.08944.pdf）

• 导向搜索

除双向扩展树策略外，Jaillet、Rodriguez等人根据环境特征诱导采样点的生成，如ADD-RRT[12]将边界点采样区限制于球体中，并建立球半径与边界点扩展成功率的映射关系，以此提升扩展成功率。OB-RRT[13]与之类似，通过收集障碍物数据以确定节点生长方向。CL-RRT[14]将闭环预测应用于RRT框架，使用了物理与/或逻辑环境来偏置高斯采样云，并被应用于MIT Talos。

• 非全向限制搜索

Karaman、Webb等人研究改进RRT算法以满足存在非全向约束条件的机器人，如Kinodynamic-RRT*[15]考虑了机器人模型硬约束，但计算内存消耗较大，Adapted RRT*[16]克服了该缺点并得到渐进最优解，可解决5D状态空间下的类车机器人和10D状态空间下飞行器的运动规划问题。RTR+C*CS[17]提供完整规划方案，RTR生成全局路径，C*CS使用直线段和圆弧拟合得到局部路径（图 2.6），但需要的迭代次数较多。针对高维度规划问题，RABIT*[18]使用同伦类生成初始路径，并采用局部优化技术达到全局优化的结果。

图 2.6 C*CS [17]

2.3CVM类算法

第三类是CVM（Curvature Velocity Method）类算法，核心思想是基于非全向移动机器人小速度空间范围，结合运动学模型，生成预测轨迹，并进行约束条件评估分析，找出最合适的轨迹。

Simmons、Ko等人针对差速移动机器人提出基于有边界的速度空间采样方法，即机器人运动轨迹为圆弧或直线。如CVM[19]在速度空间中等距采样，并选择综合成本最低的速度以控制机器人，LCM[20]针对廊道场景，将CVM与方向空间法相结合，驱动机器人沿着廊道运动的同时避开障碍物。如图 1.6所示，DCVM[21]融入概率3D占据-速度栅格图，用于避开动态障碍物，并在仿真和真实环境中得到验证。

图 2.7 DCVM[21]

2.4DWA类算法

第四类是DWA（Dynamic Window Approach）类算法，DWA[22]与CVM极为相似，均基于速度空间采样，评价方式有区别。Brock、Seder等人提出了改进算法，如General DWA[23]将DWA扩展为全向移动，并融入导航函数，TVDW[24]考虑了动态障碍物，将FD*与DWA相结合，以提升机器人运动前瞻性，DW4DO[25]使用了双重动态窗，无动力学约束限制的动态窗增加了DWA的探测范围，并将其升级为DW4DOT[25]，进一步提升DWA的前瞻性，以提升其避障性能。

图 2.8 DWA算法（图片来源：https://github.com/AtsushiSakai/PythonRobotics）

03 空间采样算法分析

从上述章节分析可以，这四类空间采样算法各有各的特点，但总体而言，PRM类和RRT类算法思路很接近，CVM类和DWA类算法思路很接近，主要区别是在部分细节处理方面。所以，主要分为下面两类算法进行分析：

PRM&RRT类

PRM&RRT类算法的核心思想就是在搜索空间中随机采样，并通过图或树的方式连接这些采样点，去掉不满足约束的连线，最后基于图或树的搜索算法生成最优路径。

• 主要优点：在高维空间下搜索效率高，概率完备且渐进最优，也就是说采样点越密集，搜索的路径越短。

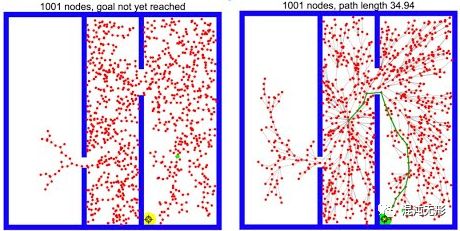
• 主要缺点：生成的路径连续性较差（基本上是折线段），在动态环境下收敛性差（需要时刻检查已经生成的图或树是否与障碍物有交集），内存消耗较大（采样点越多），狭窄区域通过性较差（如图 3.1所示）。

图 3.1 RRT通过狭窄区域（图片来源：https://www.youtube.com/watch?v=Ob3BIJkQJEw）

CVM&DWA类

CVM&DWA类算法的核心思想是基于运动空间进行采样，并结合运动学模型生成预测轨迹，评估、选择最合适的轨迹。

• 主要优点：模型简洁，实时性好（低维空间的计算量较小），严格按照运动学模型计算，生成的轨迹质量高，且动态环境避障性能强（实时性好的表现）。

• 主要缺点：基于运动学模型生成的轨迹长度短且单一，且前瞻性不足（轨迹长度偏短的表现），因为轨迹长度延长后会产生卷曲的现象，如图 3.2所示。

图 3.2 DWA生成的候选轨迹（图片来源：https://www.semanticscholar.org/paper/A-Dynamic-Window-Approach-with-Collision-Cone-for-Guan-Wen/8e2bdca7daa3938ba8277a5a7df606be84db63bc）

从上述分析可知，PRM&RRT类算法是在状态空间中采样，搜索最合适的路径，进而导出机器人在运动空间的运动参数；而CVM&DWA类算法是在运动空间中采样，生成机器人在状态空间的轨迹，进而选择最合适的轨迹，轨迹规划的目的之一就是找到一条运动空间和轨迹空间间的连接通道，让机器人在运动空间和状态空间均满足自身和环境的约束。

总体而言，空间采样算法已经能够在诸多场景下的规划生成一条无碰撞路径，比如DWA算法就被作为ROS navigation stack中local planner的默认算法，RRT算法主要应用于高维度空间的路径规划，如无人机、机械臂等领域。

随着诸多学者的改进升级，空间采样算法的实时性、轨迹质量和动态适应性逐渐提升，但多数算法仍存在路径质量差、未考虑动力学约束等问题，这些问题也导致相关算法不能直接应用于实际机器人运动场景。

04结论与展望

本文将空间采样算法拆解为四个子类算法：PRM类算法、RRT类算法、CVM类算法和DWA类算法，并沿时间先后顺序概述了相关类型算法的发展改进历程，接着从模型复杂度、计算实时性、动态环境适应能力及路径曲线质量等方面分析了上述四类算法的优缺点，并指出存在的相关问题。

运动规划算法种类繁多，应用场景各不相同，而本文仅概述分析了四类运动规划算法之一的空间采样算法，后续会分析其他类型算法。

（文章仅笔者个人分析，有误请指正，谢谢！）

参考资料

[1] REIF J, WANG H. The complexity of the two dimensional curvature-constrained shortest-path problem; proceedings of the Third International Workshop on Algorithmic Foundations of Robotics, F, 1998 [C].

[2] KAVRAKI L E, SVESTKA P, LATOMBE J-C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces [J]. IEEE transactions on Robotics and Automation, 1996, 12(4): 566-80.

[3] BOHLIN R, KAVRAKI L E. Path planning using lazy PRM; proceedings of the Proceedings 2000 ICRA Millennium Conference IEEE International Conference on Robotics and Automation Symposia Proceedings (Cat No 00CH37065), F, 2000 [C]. IEEE.

[4] DOBSON A, BEKRIS K E. Improving sparse roadmap spanners; proceedings of the 2013 IEEE International Conference on Robotics and Automation, F, 2013 [C]. IEEE.

[5] LAVALLE S M. Rapidly-exploring random trees: A new tool for path planning [J]. 1998,

[6] KARAMAN S, FRAZZOLI E. Sampling-based algorithms for optimal motion planning [J]. The international journal of robotics research, 2011, 30(7): 846-94.

[7] GAMMELL J D, SRINIVASA S S, BARFOOT T D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic; proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, F, 2014 [C]. IEEE.

[8] OTTE M, FRAZZOLI E. RRTX: Asymptotically optimal single-query sampling-based motion planning with quick replanning [J]. The International Journal of Robotics Research, 2016, 35(7): 797-822.

[9] KUFFNER J J, LAVALLE S M. RRT-connect: An efficient approach to single-query path planning; proceedings of the Proceedings 2000 ICRA Millennium Conference IEEE International Conference on Robotics and Automation Symposia Proceedings (Cat No 00CH37065), F, 2000 [C]. IEEE.

[10] JORDAN M, PEREZ A. Optimal bidirectional rapidly-exploring random trees [J]. 2013,

[11] YI D, GOODRICH M A, SEPPI K D. Homotopy-aware RRT*: Toward human-robot topological path-planning; proceedings of the 2016 11th ACM/IEEE International Conference on Human-Robot Interaction (HRI), F, 2016 [C]. IEEE.

[12] JAILLET L, YERSHOVA A, LA VALLE S M, et al. Adaptive tuning of the sampling domain for dynamic-domain RRTs; proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, F, 2005 [C]. IEEE.

[13] RODRIGUEZ S, TANG X, LIEN J-M, et al. An obstacle-based rapidly-exploring random tree; proceedings of the Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006 ICRA 2006, F, 2006 [C]. IEEE.

[14] KUWATA Y, TEO J, FIORE G, et al. Real-time motion planning with applications to autonomous urban driving [J]. IEEE Transactions on Control Systems Technology, 2009, 17(5): 1105-18.

[15] KARAMAN S, FRAZZOLI E. Optimal kinodynamic motion planning using incremental sampling-based methods; proceedings of the 49th IEEE conference on decision and control (CDC), F, 2010 [C]. IEEE.

[16] WEBB D J, VAN DEN BERG J. Kinodynamic RRT*: Asymptotically optimal motion planning for robots with linear dynamics; proceedings of the 2013 IEEE International Conference on Robotics and Automation, F, 2013 [C]. IEEE.

[17] CSORVáSI G, NAGY A, KISS D. RTR+ C* CS: An effective geometric planner for car-like robots; proceedings of the Proceedings of the 2015 16th International Carpathian Control Conference (ICCC), F, 2015 [C]. IEEE.

[18] CHOUDHURY S, GAMMELL J D, BARFOOT T D, et al. Regionally accelerated batch informed trees (rabit*): A framework to integrate local information into optimal path planning; proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), F, 2016 [C]. IEEE.

[19] SIMMONS R. The curvature-velocity method for local obstacle avoidance; proceedings of the Proceedings of IEEE international conference on robotics and automation, F, 1996 [C]. IEEE.

[20] KO N Y, SIMMONS R G. The lane-curvature method for local obstacle avoidance; proceedings of the Proceedings 1998 IEEE/RSJ International Conference on Intelligent Robots and Systems Innovations in Theory, Practice and Applications (Cat No 98CH36190), F, 1998 [C]. IEEE.

[21] MOLINOS E, LLAMAZARES Á, OCAñA M, et al. Dynamic obstacle avoidance based on curvature arcs; proceedings of the 2014 IEEE/SICE International Symposium on System Integration, F, 2014 [C]. IEEE.

[22] FOX D, BURGARD W, THRUN S. The dynamic window approach to collision avoidance [J]. IEEE Robotics & Automation Magazine, 1997, 4(1): 23-33.

[23] BROCK O, KHATIB O. High-speed navigation using the global dynamic window approach; proceedings of the Proceedings 1999 IEEE International Conference on Robotics and Automation (Cat No 99CH36288C), F, 1999 [C]. IEEE.

[24] SEDER M, PETROVIC I. Dynamic window based approach to mobile robot motion control in the presence of moving obstacles; proceedings of the Proceedings 2007 IEEE International Conference on Robotics and Automation, F, 2007 [C]. IEEE.

[25] MOLINOS E J, LLAMAZARES Á, OCAñA M. Dynamic window based approaches for avoiding obstacles in moving [J]. Robotics and Autonomous Systems, 2019, 118(112-30.

福利放送

笔者为小伙伴们整理了期刊论文版式原文PDF，方便收藏和回味

链接：https://pan.baidu.com/s/1AdAElKE7BIEP-uvfUaF1nQ

提取码：rn09

若链接失效，可在后台回复完整本文标题或发送邮件：[email protected]

延伸阅读

机器人图规划算法研究现状简述

机器人环境感知研究现状简述

常见移动机器人运动学模型总结

常见移动机器人多角度对比分析

Car-like robot运动参数校准

差速驱动机器人轮间距校准

常见移动机器人轮直径校准

全向移动机器人运动参数校准

-----------------------------------------------------------------------------

相关声明

1.如果转载本文，文末务必注明：“转自微信公众号：混沌无形”

2.若有侵权，请联系作者

全文完，感谢阅读！！如果觉得写的不错，那就点个赞或者“在看”吧。

混沌无形

混沌系统是世界本质，无形之中存在规律。机器人智能化发展从线性过渡到混沌，本号将分享机器人全栈技术（感知、规划、控制；软件、机械、硬件等）。

41篇原创内容

公众号