栈&队列&哈希表&堆-python

一、栈

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。
栈的主要操作：

push()，将新的元素压入栈顶，同时栈顶上升。
pop()，将新的元素弹出栈顶，同时栈顶下降。
empty()，栈是否为空。
peek()，返回栈顶元素。

python通常实现栈只需要list就可以，list.append(val), list.pop()、list[-1]

支持操作：O(1) Push / O(1) Pop / O(1) Top

1、如何用list实现一个栈

class Stack:
    def __init__(self):
        self.nums= []
				
    # 压入元素
    def push(self, x):
        self.nums.append(x)
    
    # 栈顶元素出栈
    def pop(self):
        if not self.is_empty():
            self.nums.pop()
	
    # 返回栈顶元素
    def top(self):
        return self.nums[-1]

    # 判断是否是空栈
    def is_empty(self):
        return len(self.nums) == 0

2、如何用两个队列实现一个栈？

from collections import deque

class Stack:
    def __init__(self):
        self.queue1 = deque()
        self.queue2 = deque()

    def push(self, x):
        self.queue1.append(x)

    def pop(self):
         # 元素转移 
        while len(self.queue1) != 1:
            self.queue2.append(self.queue1.popleft())
        self.queue1.popleft()
        self.queue1, self.queue2 = self.queue2, self.queue1

    def top(self):
         # 元素转移 
        while len(self.queue1) != 1:
            self.queue2.append(self.queue1.popleft())
        item = self.queue1.popleft()
        self.queue1, self.queue2 = self.queue2, self.queue1
        self.queue1.append(item)
        return item

    def is_empty(self):
        return len(self.queue1) == 0

3、单调栈

单调栈的应用：https://blog.csdn.net/qq_19446965/article/details/104720836

其余栈的应用：

接雨水：https://blog.csdn.net/qq_19446965/article/details/104144187

矩阵中最大矩形：https://blog.csdn.net/qq_19446965/article/details/82048028

基本计算器类：https://blog.csdn.net/qq_19446965/article/details/104717537

4、用一个数组如何实现三个栈？（挑战）

不介绍，参照九章算法

二、队列

队列为一种先进先出的线性表
只允许在表的一端进行入队，在另一端进行出队操作。在队列中，允许插入的一端叫队尾，允许删除的一端叫队头，即入队只能从队尾入，出队只能从队头出

Python四种类型的队例：

Queue：FIFO 即first in first out 先进先出

LifoQueue：LIFO 即last in first out 后进先出

PriorityQueue：优先队列，级别越低，越优先

deque:双边队列

from queue import Queue,LifoQueue,PriorityQueue
from collections import deque

https://www.cnblogs.com/rnanprince/p/11588359.html

支持操作：O(1) Push / O(1) Pop / O(1) Top

队列通常被用作 BFS 算法的主要数据结构。

1、如何用链表实现队列

需要一个头部节点，也就是dummy节点，即dummy.next为第一个元素，还需要一个尾部节点，即tail节点，表示的是最后一个元素的节点
初始化：tail和dummy都指向头部
增加元素：即从队尾中加入一个元素，则要建一个值为val的node节点，然后tail.next=node，再移动tail节点到tail.next
删除元素：将dummy.next变为dummy.next.next，即可删掉了第一个元素，这里tail与dummy可能重新重合（当只有一个元素时）
队头元素peek() : dummy.next.val

class Node:
    def __init__(self, value):
        self.val = value
        self.next = None


class Queue:
    def __init__(self):
        self.dummy = Node(-1)
        self.tail = self.dummy
    
    # 入队操作 
    def enqueue(self, val):
        node = Node(val)
        self.tail.next = node
        self.tail = node

    # 出队操作
    def dequeue(self):
        first = self.dummy.next.val
        self.dummy.next = self.dummy.next.next

        if not self.dummy.next:
            self.tail = self.dummy
        return first 

    def peek(self):
        return self.dummy.next.val

    def is_empty(self):
        return not self.dummy.next

2、如何用循环数组实现队列？

循环数组类似循环链表，首尾相连

两个变量：front——>队头 rear ——>队尾
增加元素时，如果 rear 到达末尾，即 rear= array.length - 1 ，rear 需要更新为 0；删除元素时，如果 front = array.length - 1, front 需要更新为 0。

class CircularQueue:
    def __init__(self, n):
        self.nums= [0 for _ in range(n)]
        self.front = 0
        self.rear = 0
        self.size = 0
        
    def is_full(self):
        return self.size == len(self.nums)

    def is_empty(self):
        return self.size == 0

    def enqueue(self, val):
        if self.is_full():
            print("Queue is already full")
        # 计算下一个队尾位置
        self.rear = (self.front+self.size) % len(self.nums)
        self.nums[self.rear] = val
        self.size += 1

    def dequeue(self):
        if self.is_empty():
            print("Queue is already empty")
        first= self.nums[self.front]
        self.front = (self.front+1) % len(self.nnums)
        self.size -= 1
        return first

3、经典问题

滑动窗口的最大值: https://www.jiuzhang.com/solution/sliding-window-maximum/#tag-highlight-lang-python（优先单调队列，或双边单调递减栈）

总结：https://www.cnblogs.com/rnanprince/p/11832071.html

三、哈希表

介绍一下哈希表原理中的几个重要的知识点：

哈希表的工作原理
哈希函数（Hash Function）该如何实现
为什么 hash 上各种操作的时间复杂度不能单纯的认为是 O(1) 的
哈希冲突（Collision）该如何解决
如何让哈希表可以不断扩容？

1、哈希表的工作原理

哈希表又称散列表。哈希表存储的基本思想是：以数据表中的每个记录的关键字 k为自变量，通过一种函数H(k)计算出函数值。把这个值解释为一块连续存储空间（即数组空间）的单元地址（即下标），将该记录存储到这个单元中。在此称该函数H为哈希函数或散列函数。按这种方法建立的表称为哈希表或散列表。

哈希一般分两步执行：

通过使用哈希函数将元素转换为整数。此元素可用作存储原始元素的索引，该元素属于哈希表。
元素存储在哈希表中，可以使用哈希键快速检索它。

hash = hashfunc（key）

index = hash％array_size

在此方法中，哈希与数组大小无关，然后通过使用模运算符（％）将其缩减为索引（介于0和array_size - 1之间的数字）。

2、哈希函数（Hash Function）该如何实现

Python的hashCode函数实现：

def hashCode(s):
    seed = 31
    h = 0
    for c in s:
        h = int32(seed * h) + ord(c)

    return h

3、为什么 hash 上各种操作的时间复杂度不能单纯的认为是 O(1) 的

整数没问题O(1)，string就是O(size of key)

4、处理冲突的方法：

开放寻址法：Hi=(H(key) + di) MOD m, i=1,2,…, k(k<=m-1)，其中H(key)为散列函数，m为散列表长，di为增量序列，可有下列三种取法：

1.di=1,2,3,…, m-1，称线性探测再散列；

2.di=1^2, -1^2, 2^2,-2^2, 3^2, …, ±(k)^2,(k<=m/2)称二次探测再散列；

3.di=伪随机数序列，称伪随机探测再散列。

再散列法：Hi=RHi(key), i=1,2,…,k. RHi均是不同的散列函数，即在同义词产生地址冲突时计算另一个散列函数地址，直到冲突不再发生，这种方法不易产生“聚集”，但增加了计算时间；

链地址法（拉链法）：将所有关键字为同义词的记录存储在同一线性链表中；

例：设哈希表长为14，哈希函数是H(key)=key%11,表中已有数据的关键字为15，38，61，84共四个，现要将关键字为49的结点加到表中，用二次探测再散列法解决冲突，则放入的位置是( ) 【南京理工大学 2001 一、15 （1.5分）】

A．8 B．3 C．5 D．9
答案为A,为什么我计算出来是D呢?
我的计算步骤如下:
15，38，61，84用哈希函数H(key)=key%11计算后得地址:4,5,6,7
49计算后为5,发生冲突.
用二次探测再散列法解决冲突:
1:(key+1^2)%11=(49+1)%11=6,仍然发生冲突.
2:(key-1^2)%11=(49-1)%11=4,仍然发生冲突.
3:(key+2^2)%11=(49+4)%11=9,不再发生冲突.
得出结果为D

5、如何让哈希表可以不断扩容？

什么是 Rehashing（重哈希）？

哈希表容量的大小在一开始是不确定的。如果哈希表存储的元素太多（如超过容量的十分之一），我们应该将哈希表容量扩大一倍，并将所有的哈希值重新安排。
假设你有如下一哈希表：
size=3, capacity=4

[null, 21, 14, null]
        ↓    ↓
        9   null
        ↓
      null

哈希函数为：

 def hashcode(key, capacity):
      return key % capacity

这里有三个数字9，14，21，其中21和9共享同一个位置因为它们有相同的哈希值1
(21 % 4 = 9 % 4 = 1)。我们将它们存储在同一个链表中。
重建哈希表，将容量扩大一倍，我们将会得到：
size=3, capacity=8
index: 0 1 2 3 4 5 6 7
hash : [null, 9, null, null, null, 21, 14, null]
给定一个哈希表，返回重哈希后的哈希表。

6、哈希表相关题目：

https://www.cnblogs.com/rnanprince/p/11878854.html

四、堆

最小堆是一棵完全二叉树，非叶子结点的值不大于左孩子和右孩子的值

log(n) ——>add() 插入

log(n) ——>pop() 删除

O(1)——>min、max

构建一个 heap 的时间复杂度？

是 O(n) 还是 O(nlogn) ?
是 O(n)，用 Heapify
Python: heapq.heapify([...])

遍历一个 heap 的时间复杂度？
比如 Java 中可以用 Iterator 来遍历

O(nlogn)

分类: 大顶堆（最大堆）、小顶堆（最小堆）

以最小堆为例：

father = (child - 1) // 2

child_left = 2*father + 1 child_right = 2*father + 2

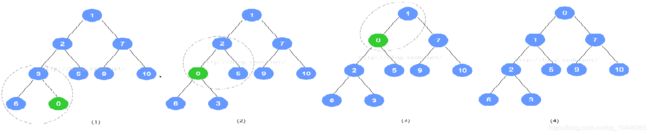
1、插入

以上个最小堆为例，插入数字0。数字0的节点首先加入到该二叉树最后的一个节点，依据最小堆的定义，自底向上，递归调整。

    # 向上调整
    def  siftup(self, A, child):
        while child != 0:
            father = (child - 1) // 2
            if A[child] > A[father]:
                break

            A[child], A[father] = A[child], A[father]
            child = father

步骤：

对于每个元素A[i]，比较A[i]和它的父亲结点的大小，如果小于父亲结点，则与父亲结点交换。
交换后再和新的父亲比较，重复上述操作，直至该点的值大于父亲

2、删除

对于删除操作，将二叉树的最后一个节点替换到根节点，然后自顶向下，递归调整。

    # 向下调整
    def siftdown(self, A, father):
        while father * 2 + 1 < len(A):
            # 选择两个孩子中较小的一个，进行交换
            child = father * 2 + 1    # A[i]左孩子的下标
            child_right = father * 2 + 2    # A[i]右孩子的下标
            if child_left < len(A) and A[child_left] > A[child_right]:
                child = child_right  
  
            if A[child] >= A[k]:
                break
                
            A[child], A[father] = A[father], A[child]
            father = child

步骤：

初始选择最接近叶子的一个父结点，与其两个孩子中较小的一个比较，若大于孩子，则与孩子交换。
交换后再与新的孩子比较并交换，直至没有孩子。
再选择较浅深度的父亲结点，重复上述步骤。

3、堆相关题目

https://www.cnblogs.com/rnanprince/p/11879690.html

4、堆排序：

经典问题总结：