三、Pytorch多层感知机 （3月1日学习笔记）

首先，多层感知机相当于在输入层和输出层中间添加一个到多个隐藏层。其中，隐藏层和输出层都是全连接层。

但是，如果只在其中插入多个简单全连接层相当于还是只有一层全连接层，因为每层对其输入和得到输出为：H=X*W1 + b1，在下一层为O=H*W2 + b2，综合来看是O=X*W1*W2 + b1*W2 +b2。将各矩阵和向量整体来看，仍然相当于一层全连接层。

所以明白了“多个仿射变换叠加仍然是一个仿射变换”这句话。

解决这个问题的方法就是引入非线性函数进行变换，即激活函数。

激活函数

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活，它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。由于激活函数是深度学习的基础，下面是常见的激活函数)。

%matplotlib inline
import torch
from d2l import torch as d2l

ReLU函数

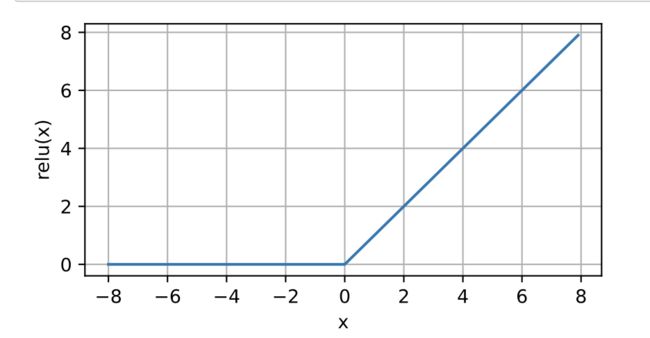
最受欢迎的激活函数是修正线性单元（Rectified linear unit，ReLU），因为它实现简单，同时在各种预测任务中表现良好。ReLU函数通过将相应的活性值设为0，仅保留正元素并丢弃所有负元素。正如从图中所看到，激活函数是分段线性的。

***注意：使用requires_grad=True来跟踪变量x的梯度，而detach()方法分离两变量，使用当前值。然后backward()方法自动求梯度，需传入一个和变量一样维度的矩阵。

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。注意，当输入值精确等于0时，ReLU函数不可导。在此时，我们默认使用左侧的导数，即当输入为0时导数为0。我们可以忽略这种情况，因为输入可能永远都不会是0。

下面是ReLU函数的导数。

y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。

sigmoid函数

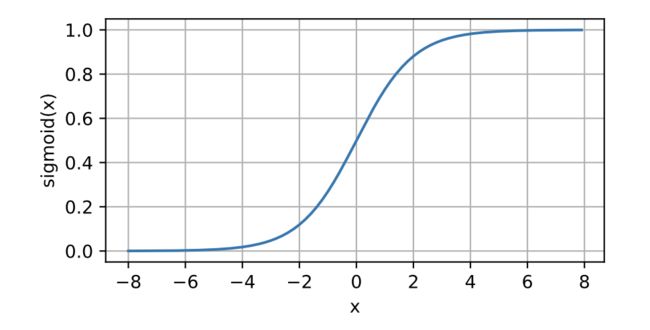
对于一个定义域在正负无穷中的输入，sigmoid函数将输入变换为区间(0, 1)上的输出因此，sigmoid通常称为挤压函数（squashing function）：它将范围（-inf, inf）中的任意输入压缩到区间（0, 1）中的某个值。（sigmoid可以视为softmax的特例）。

然而，sigmoid在隐藏层中已经较少使用，

y = torch.sigmoid(x)
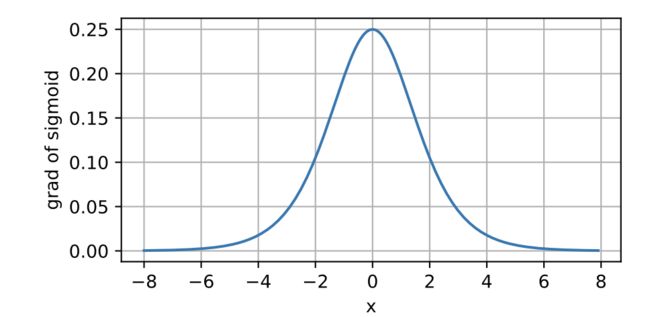
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

sigmoid函数的导数图像如下所示。

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))

tanh函数

与sigmoid函数类似，

[tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上]。当输入在0附近时，tanh函数接近线性变换。函数的形状类似于sigmoid函数，不同的是tanh函数关于坐标系原点中心对称。

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

tanh函数的导数是：

tanh函数的导数图像如下所示。当输入接近0时，tanh函数的导数接近最大值1。与我们在sigmoid函数图像中看到的类似，输入在任一方向上越远离0点，导数越接近0。

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))

总结一下，我们现在了解了如何结合非线性函数来构建具有更强表达能力的多层神经网络架构。

小结

• 多层感知机在输出层和输入层之间增加一个或多个全连接隐藏层，并通过激活函数转换隐藏层的输出。

• 常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。