基于决策树的银行存款预测
文章目录
- 前言
- 一、决策树是什么?
- 二、实验原理
- 三、具体实现
-
- 1.求每个特征的信息熵
- 2.求每个特征信息增益并找寻信息增益最大的特征值
- 3.实现决策树的网络结构并保存
- 4.模型中未出现的判决条件情况下,结果确定
- 5.预测函数
- 6.对银行数据进行预测
- 四、实现结果
- 五、结果分析
- 六、源码
前言
本文主要介绍了决策树的具体实现过程,其中主要包括单特征信息熵的计算、信息增益的计算、决策树的建立及模型保存、模型训练和预测,最后通过对银行存款预测来检测建立的模型。
银行存款数据集:机器学习——决策树数据2
一、决策树是什么?
决策树(Decision Tree):是一种树形归纳分类算法,通过对训练集数据的学习,挖掘出一定的规则,用于对测试集数据进行预测.
决策树是一种典型的分类方法
1)首先对数据进行处理,利用归纳算法生成可读的规则和决策树,
2)然后使用决策对新数据进行分析。
本质上决策树是通过一系列规则对数据进行分类的过程。
二、实验原理
分别对各个特征求取他们的信息增益,对信息增益最明显(最大值)的特征作为当前的划分特征,并根据该特征下各个元素,将原表分为各个子表,重复上述步骤,直至表中的标签只含一个值,或达到所设定的阈值。建立决策树之后,将经过预处理的数据放入模型中进行预测,并对预测结果和标签进行对比,分析结果。
三、具体实现
1.求每个特征的信息熵
代码如下(示例):
import math
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
# 计算信息熵
def Ent(data, feature, target): # data为dataframe型,feature:特征(字符串),target:标签(字符串)
data = data.loc[:, [feature, target]] #选出特征列和标签列
data_target = set(data.loc[:, target].values)
len1 = data.shape[0] #len1:总行数
sum = 0
for i in data_target:
len2 = data[data[target] == i].shape[0] #len2:该特征下i结果的行数
if len2/len1 != 1:
sum += -(len2/len1)*math.log2(len2/len1)
return sum
2.求每个特征信息增益并找寻信息增益最大的特征值
随着树的深度的增加,结点的熵迅速降低,熵降低的越快越好,这样我们有望得到一棵高度最矮的决策树
![]()
代码如下(示例):
# 计算信息增益
def Gain(data, feature, target):
#计算划分前信息熵
s0 = Ent(data, feature, target)
#计算划分后的信息熵
tz_set = set(data.loc[:, feature].values) #特征所有可能的取值
count = data.shape[0] #划分前数据表中所有行数
sum = 0 # 保存划分后信息熵与所占比乘积之和
for i in tz_set:
data_temp = data[data[feature] == i]
count_temp = data_temp.shape[0] #划分后数据表中所有行数
sum += (count_temp/count) * Ent(data_temp, feature, target)
return s0-sum # 返回信息增益
# 寻找信息增益最大的特征值
def Get_MaxGain(data, target):
column = data.columns
max = 0
for i in column: # 计算各个特征的信息增益
if i == target:
continue
sum = Gain(data, i, target)
if sum>max:
max = sum
max_feature = i
return max_feature
3.实现决策树的网络结构并保存
由于python没有专门的树形结构,所以我才用列表的形式保存树,该列表由三部分构成,分别是特征名称、特征值、该特征值下的下一层结构,[特征名称, 特征值1,[特征值1的下一层结构],特征值2,[特征值2的下一层结构],…,特征值n, [特征值n的下一层结构]]。
例如:

该决策树结构为:[‘年龄’, ‘大于20岁’, [‘身高’, ‘大于180cm’, [‘结果’, 0], ‘小于180cm’, [‘结果’, 1]], ‘小于20岁’, [‘体重’, ‘小于50kg’, [‘结果’, 0], ‘大于70kg’, [‘结果’, 1]]]
# 递归实现决策树的网络结构并保存
def DisTree(data, target, k, ListTree): # k:格式化输出
ListNode = [] # 叶节点
if len(set(data.loc[:, target])) == 1:
ListNode.append('结果') # 添加结果结点,同时也是决策树最底层结果的标识
ListNode.append(data.loc[:, target].values[0])
# print('{}结果为:{}'.format((k-1)*2*' ', data.loc[:, target].values[0]))
ListTree.append(ListNode) # 将叶节点添加到树中
return ListTree
if k==6: # 树结构为五层判别条件,一层结果
ListNode.append('结果')
ListNode.append(list(data[target].mode())[0]) # 找到target里面的众数,不存在众数的情况下找出任意一个
# print('{}结果为:{}'.format((k-1)*2*' ', list(data[target].mode())[0]))
ListTree.append(ListNode) # 将叶节点添加到树中
return ListTree
feature = Get_MaxGain(data, target) # 目前表中最佳分类的特征
ListNode.append(feature) # 添加特征
tz_set = set(data.loc[:, feature].values) #特征所有可能的取值
for i in tz_set:
# print('{}当{}为{}时'.format((k-1)*2*' ', feature, i))
ListNode.append(str(i)) # 添加条件
data_temp = data[data[feature] == i]
DisTree(data_temp, target, k+1, ListNode)
ListTree.append(ListNode) # 将叶节点添加到树中
return ListTree
# 规范化训练函数
def fit(data, target):
model = DisTree(data, target, 1,[])
return model
4.模型中未出现的判决条件情况下,结果确定
由于数据预处理时不太合理会导致预测时遇到一些从未出现的情况,这个时候采用及时终止—就地分析的策略,数据在该层的预测到此位置,但结果的产生依据模型中该层以下所有结果,在这些结果中采用等权投票的方法,选出最佳结果作为该数据的预测结果。
例如:当遇见年龄为68的时候

结果为:0
# 模型中未出现的判决条件情况下,结果确定
def Not_in_model(model, result):
if(model[0] == '结果'):
result.append(model[1])
return result
m = 2
while(m<len(model)):
Not_in_model(model[m], result)
m += 2
return result
5.预测函数
根据训练的模型,对待预测的每条数据进行预测,根据模型中的每个特征名称,寻找待预测数据该特征下的特征值,根据该特征值在列表中寻找对应索引,索引值加一即为下一层的结构,根据下一层的特征名称继续进行寻找,直至找到特征名称为“结果”的列表,表明已找到决策树的最低层—结果层,该列表下标为1的位置对应为预测结果。
#预测函数
def predict(model, data):
result = [] # 预测的结果保存
for i in range(len(data)): # 对每条数据进行预测
models = model[0]
feature = models[0] # 第一个需要判别的特征名称
while feature != '结果':
# print(" \n"*5) # 显示模型变化
# print(models)
value = str(data.loc[data.index[i], feature]) # 找出该数据的feature对应的值
try:
k = models.index(value) # 在模型中找到value对应的下标
except: # 如果该选项未出现,则到判定此为止,开始分析结果
temp = Not_in_model(models,[])
result.append(max(temp, default='列表为空', key=lambda v: temp.count(v)))
break
models = models[k+1] # 根据model的结构树,value值对应下一个索引值为下一层的判决条件
feature = models[0]
if models[0] == '结果':
result.append(models[1])
return result
6.对银行数据进行预测
1)对数据进行与处理
分析各连续值特征的分布规律对其进行划分
对特征’balance’:
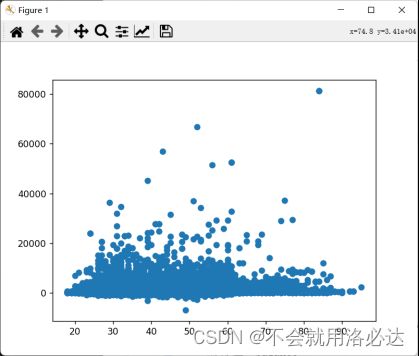
# 数据处理
data.drop('day', axis = 1, inplace= True)
data.drop('month', axis = 1, inplace= True)
data.loc[data["age"]<=18,"age"]=0
data.loc[data["age"]>50,"age"]=2
data.loc[data["age"]>18,"age"]=1
data.loc[data["balance"]<=20000,"balance"]=0
data.loc[data["balance"]>40000,"balance"]=2
data.loc[data["balance"]>20000,"balance"]=1
data.loc[data["duration"]<=500,"duration"]=0
data.loc[data["duration"]>2000,"duration"]=2
data.loc[data["duration"]>500,"duration"]=1
data.loc[data['previous']<=10,'previous']=0
data.loc[data['previous']>20,'previous']=2
data.loc[data['previous']>10,'previous']=1
data.loc[data['campaign']<=10,'campaign']=0
data.loc[data['campaign']>20,'campaign']=2
data.loc[data['campaign']>10,'campaign']=1
data.loc[data['pdays']<=200,'pdays']=0
data.loc[data['pdays']>400,'pdays']=2
data.loc[data['pdays']>200,'pdays']=1
2)划分训练集、测试集,并训练及对测试机进行预测
X_train, X_test, y_train, y_test = train_test_split(data, data.loc[:, target],test_size=0.25, random_state=7)
model = fit(X_train, target)
print(model)
result = predict(model, X_test)
score(result, y_test)
四、实现结果
![]()
五、结果分析
1、由于数据处理的时候不够精细导致结果误差较大。
2、模型保存重复值出现次数太多,列表保存树结构不是一个很好的解决方案。
六、源码
import math
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
# 计算信息熵
def Ent(data, feature, target): # data为dataframe型,feature:特征(字符串),target:标签(字符串)
data = data.loc[:, [feature, target]] #选出特征列和标签列
data_target = set(data.loc[:, target].values)
len1 = data.shape[0] #len1:总行数
sum = 0
for i in data_target:
len2 = data[data[target] == i].shape[0] #len2:该特征下i结果的行数
if len2/len1 != 1:
sum += -(len2/len1)*math.log2(len2/len1)
return sum
# 计算信息增益
def Gain(data, feature, target):
#计算划分前信息熵
s0 = Ent(data, feature, target)
#计算划分后的信息熵
tz_set = set(data.loc[:, feature].values) #特征所有可能的取值
count = data.shape[0] #划分前数据表中所有行数
sum = 0 # 保存划分后信息熵与所占比乘积之和
for i in tz_set:
data_temp = data[data[feature] == i]
count_temp = data_temp.shape[0] #划分后数据表中所有行数
sum += (count_temp/count) * Ent(data_temp, feature, target)
return s0-sum # 返回信息增益
# 寻找信息增益最大的特征值
def Get_MaxGain(data, target):
column = data.columns
max = 0
for i in column: # 计算各个特征的信息增益
if i == target:
continue
sum = Gain(data, i, target)
if sum>max:
max = sum
max_feature = i
return max_feature
# 递归实现决策树的网络结构并保存
def DisTree(data, target, k, ListTree): # k:格式化输出
ListNode = [] # 叶节点
if len(set(data.loc[:, target])) == 1:
ListNode.append('结果') # 添加结果结点,同时也是决策树最底层结果的标识
ListNode.append(data.loc[:, target].values[0])
# print('{}结果为:{}'.format((k-1)*2*' ', data.loc[:, target].values[0]))
ListTree.append(ListNode) # 将叶节点添加到树中
return ListTree
if k==6: # 树结构为五层判别条件,一层结果
ListNode.append('结果')
ListNode.append(list(data[target].mode())[0]) # 找到target里面的众数,不存在众数的情况下找出任意一个
# print('{}结果为:{}'.format((k-1)*2*' ', list(data[target].mode())[0]))
ListTree.append(ListNode) # 将叶节点添加到树中
return ListTree
feature = Get_MaxGain(data, target) # 目前表中最佳分类的特征
ListNode.append(feature) # 添加特征
tz_set = set(data.loc[:, feature].values) #特征所有可能的取值
for i in tz_set:
# print('{}当{}为{}时'.format((k-1)*2*' ', feature, i))
ListNode.append(str(i)) # 添加条件
data_temp = data[data[feature] == i]
DisTree(data_temp, target, k+1, ListNode)
ListTree.append(ListNode) # 将叶节点添加到树中
return ListTree
# 规范化训练函数
def fit(data, target):
model = DisTree(data, target, 1,[])
return model
# 模型中未出现的判决条件情况下,结果确定
def Not_in_model(model, result):
if(model[0] == '结果'):
result.append(model[1])
return result
m = 2
while(m<len(model)):
Not_in_model(model[m], result)
m += 2
return result
#预测函数
def predict(model, data):
result = [] # 预测的结果保存
for i in range(len(data)): # 对每条数据进行预测
models = model[0]
feature = models[0] # 第一个需要判别的特征名称
while feature != '结果':
# print(" \n"*5) # 显示模型变化
# print(models)
value = str(data.loc[data.index[i], feature]) # 找出该数据的feature对应的值
try:
k = models.index(value) # 在模型中找到value对应的下标
except: # 如果该选项未出现,则到判定此为止,开始分析结果
temp = Not_in_model(models,[])
result.append(max(temp, default='列表为空', key=lambda v: temp.count(v)))
break
models = models[k+1] # 根据model的结构树,value值对应下一个索引值为下一层的判决条件
feature = models[0]
if models[0] == '结果':
result.append(models[1])
return result
#结果显示
def score(result, target):
error = 0
for i in range(len(result)):
if result[i] != target[target.index[i]]:
# print(target[target.index[i]],result[i])
error += 1
print(result)
print('错误数为:{},错误率为:{}'.format(error, error/len(result)))
def test():
data = pd.read_csv(r'D:\python111\机器学习\课设\bank.csv')
target = data.columns.values[-1]
# 数据处理
data.drop('day', axis = 1, inplace= True)
data.drop('month', axis = 1, inplace= True)
data.loc[data["age"]<=18,"age"]=0
data.loc[data["age"]>50,"age"]=2
data.loc[data["age"]>18,"age"]=1
data.loc[data["balance"]<=20000,"balance"]=0
data.loc[data["balance"]>40000,"balance"]=2
data.loc[data["balance"]>20000,"balance"]=1
data.loc[data["duration"]<=500,"duration"]=0
data.loc[data["duration"]>2000,"duration"]=2
data.loc[data["duration"]>500,"duration"]=1
data.loc[data['previous']<=10,'previous']=0
data.loc[data['previous']>20,'previous']=2
data.loc[data['previous']>10,'previous']=1
data.loc[data['campaign']<=10,'campaign']=0
data.loc[data['campaign']>20,'campaign']=2
data.loc[data['campaign']>10,'campaign']=1
data.loc[data['pdays']<=200,'pdays']=0
data.loc[data['pdays']>400,'pdays']=2
data.loc[data['pdays']>200,'pdays']=1
print(data)
X_train, X_test, y_train, y_test = train_test_split(data, data.loc[:, target],test_size=0.25, random_state=7)
model = fit(X_train, target)
print(model)
result = predict(model, X_test)
score(result, y_test)
test()







