【Python】torch.einsum()解析

【Python】torch.einsum()解析

1. 介绍

爱因斯坦简记法：是一种由爱因斯坦提出的，对向量、矩阵、张量的求和运算 $\sum$ 的求和简记法。在该简记法当中，省略掉的部分是：

• 求和符号
• 求和号的下标

省略规则为：默认成对出现的下标（如下例1中的i和例2中的k）为求和下标。

• 表示向量内积：
  
  其中o为输出。

• 表示矩阵乘法：
  
  其中${\text{O}}_{ij}$为输出矩阵的第 i 行第 j 列的元素。

这样的求和简记法，能够以一种统一的方式表示各种各样的张量运算（内积、外积、转置、点乘、矩阵的迹、其他自定义运算），为不同运算的实现提供了一个统一模型。numpy和pytorch都对它进行了实现。

2. 示例

2.1 Pytorch矩阵乘法

例子对应的公式为：

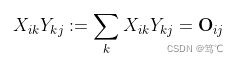
其隐含语义：输入a,b下标中相同的k，是求和的下标。

import torch
a_tensor = torch.Tensor([[11, 12, 13, 14],
				        [21, 22, 23, 24],
				        [31, 32, 33, 34],
				        [41, 42, 43, 44]])
 
b_tensor = torch.Tensor([[1, 1, 1, 1],
				        [2, 2, 2, 2],
				        [3, 3, 3, 3],
				        [4, 4, 4, 4]])
''' 
'ik, kj -> ij' 语义解释如下：
# 输入a_tensor: 2维数组，下标为ik
# 输入b_tensor: 2维数组，下标为kj
# 输出output：2维数组，下标为ij
'''
output = torch.einsum('ik, kj -> ij', a_tensor, b_tensor)
 
print(output)

tensor([[130, 130, 130, 130],
        [230, 230, 230, 230],
        [330, 330, 330, 330],
        [430, 430, 430, 430]])

2.2 Numpy高阶张量

例子对应的公式为：

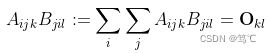
其语义为：O第k，l个元素：是矩阵 A[:,:,k] 和矩阵 B[:,:,l] 转置，对应元素相乘再求和。

import numpy as np
a = np.arange(60.).reshape(3,4,5)
b = np.arange(24.).reshape(4,3,2)

'''
# 语义解析：
# 输入a：3阶张量，下标为ijk
# 输入b: 3阶张量，下标为jil
# 输出o: 2阶张量，下标为k和l
'''
o = np.einsum('ijk,jil->kl', a, b)
print(o)
 
array([[4400., 4730.],
       [4532., 4874.],
       [4664., 5018.],
       [4796., 5162.],
       [4928., 5306.]])
 
# 验证：
print(np.sum(a[:,:,2]*b[:,:,0].T))
 
4664.0
 
print(np.sum(a[:,:,3]*b[:,:,0].T))
 
4796.0

3. 参考

【1】https://blog.csdn.net/a2806005024/article/details/96462827