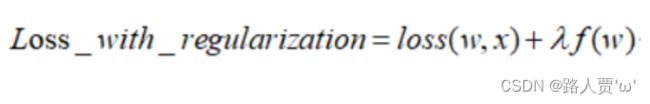Pytorch学习笔记(8):正则化(L1、L2、Dropout)与归一化(BN、LN、IN、GN)
目录
一、正则化之weight_decay(L2正则)
1.1 正则化及相关概念
1.2 正则化策略(L1、L2)
(1)L1正则化
(2)L2正则化
1.3 L2正则项——weight_decay
二、正则化之Dropout
2.1 Dropout概念
2.2 nn.Dropout
三、归一化之Batch Normalization(BN层)
3.1 Batch Normalization介绍
3.2 Pytorch的Batch Normalization 1d/2d/3d实现
(1)nn.BatchNorm1d input = B * 特征数 * 1d特征
(2)nn.BatchNorm1d input = B * 特征数 * 2d特征
(3)nn.BatchNorm1d input = B * 特征数 * 3d特征
四、归一化之Normalization_layers
4.1Layer Normalization(LN)
nn.LayerNorm
4. 2Instance Normalization(IN)
nn.InstanceNorm
4.3 Group Normalization(GN)
nn.GroupNorm
前期回顾
Pytorch学习笔记(1):基本概念、安装、张量操作、逻辑回归
Pytorch学习笔记(2):数据读取机制(DataLoader与Dataset)
Pytorch学习笔记(3):图像的预处理(transforms)
Pytorch学习笔记(4):模型创建(Module)、模型容器(Containers)、AlexNet构建
Pytorch学习笔记(5):torch.nn---网络层介绍(卷积层、池化层、线性层、激活函数层)
Pytorch学习笔记(6):模型的权值初始化与损失函数
Pytorch学习笔记(7):优化器、学习率及调整策略、动量
一、正则化之weight_decay(L2正则)
1.1 正则化及相关概念
Regularization,中文翻译过来可以称为正则化,或者是规范化。什么是规则?闭卷考试中不能查书,这就是规则,一个限制。同理,在这里,规则化就是说损失函数加上一些限制,通过这种规则去规范他们再接下来的循环迭代中,不要自我膨胀。
介绍正则化之前,我们先来了解泛化误差:
泛化误差可分解为偏差、方差与噪声,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。即泛化误差=偏差+方差+噪声
- 偏差:度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力
- 方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响
- 噪声:表达了在当前任务上任何学习算法所能够达到的期望泛化误差的下界,即刻画了学习问题本身的难度。
那么偏差、方差与我们的数据集划分到底有什么关系呢?
- 1、训练集的错误率较小,而验证集/测试集的错误率较大,说明模型存在较大方差,可能出现了过拟合
- 2、训练集和测试集的错误率都较大,且两者相近,说明模型存在较大偏差,可能出现了欠拟合
- 3、训练集和测试集的错误率都较小,且两者相近,说明方差和偏差都较小,这个模型效果比较好。
所以我们最终总结,方差一般指的是数据模型得出来了,能不能对未知数据的扰动预测准确。而偏差说明在训练集当中就已经误差较大了,基本上在测试集中没有好的效果。
通过分析,我们可以看出,正则化是用来防止模型过拟合而采取的手段。我们对代价函数增加一个限制条件,限制其较高次的参数大小不能过大。
1.2 正则化策略(L1、L2)
(1)L1正则化
L1正则化,又称Lasso Regression,是指权值向量w中各个元素的绝对值之和。比如:向量A=[1,-1,3], 那么A的L1范数为 |1|+|-1|+|3|。
L1正则化可以让一部分特征的系数缩小到0,所以L1适用于特征之间有关联的情况可以产生稀疏权值矩阵(很多权重为0,则一些特征被过滤掉),即产生一个稀疏模型,可以用于特征选择。L1也可以防止过拟合。
Q:L1为什么会产生一个稀疏权值矩阵呢?
L1正则化是权值的 绝对值之和,所以L1是带有绝对值符号的函数,因此是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当我们在原始损失函数后添加L1正则化项时,相当于对损失函数做了一个约束。
公式如下:
λ是正则化系数,是一个超参数,调节惩罚的力度,越大则惩罚力度越大。
此时我们的任务变成在约束下求出取最小值的解。
考虑二维的情况,即只有两个权值和 ,此时对于梯度下降法,求解函数的过程可以画出等值线,同时L1正则化的函数可以在二维平面上画出来。如下图:
蓝色圆圈线是Loss中前半部分待优化项的等高线,就是说在同一条线上其取值相同,且越靠近中心其值越小。
黄色菱形区域是L1正则项约束条件。
带有正则化的loss函数的最优解要在黄色菱形区域和蓝色圆圈线之间折中,也就是说最优解出现在图中优化项等高线与约束条件相交处。从图中可以看出,当待优化项的等高线逐渐向正则项约束区域扩散时,L1正则化的交点大多在坐标轴上,则很多特征维度上其参数w为0,因此会产生稀疏解;而正则化前面的系数,可以控制图形的大小。越小,约束项的图形越大(上图中的黄色方框);越大,约束项的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值中的可以取到很小的值。
(2)L2正则化
L2正则化,指权值向量中各个元素的平方和然后再求平方根,对参数进行二次约束,参数w变小,但不为零,不会形成稀疏解 。它会使优化求解稳定快速,使权重平滑。所以L2适用于特征之间没有关联的情况。 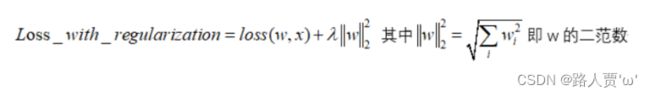 同样,L2正则化的函数也可以在二维平面上画出来,圆心就是样本值,半径就是误差,而约束条件则就是红色边界。等高线与约束条件相交的地方就是最优解。
同样,L2正则化的函数也可以在二维平面上画出来,圆心就是样本值,半径就是误差,而约束条件则就是红色边界。等高线与约束条件相交的地方就是最优解。
蓝色圆圈线和上面一样
黄色圆形区域是L2正则项约束条件。
同样,最优解出现在图中优化项等高线与正则化区域相交处。从图中可以看出,当待优化项的等高线逐渐向正则项限制区域扩散时L2正则化的交点大多在非坐标轴上,二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此与相交时使得或等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
总结:
(1)使用L1正则化在取得最优解的时候w1的值为0,相当于去掉了一个特征,而使用L2正则化在取得最优解的时候特征参数都有其值。
(2)L1会趋向于产生少量的特征,而其他的特征都为0,而L2会选择更多的特征,特征值都趋近于0。
1.3 L2正则项——weight_decay
从直观上讲,L2正则化(weight_decay)使得训练的模型在兼顾最小化分类(或其他目标)的Loss的同时,使得权重w尽可能地小,从而将权重约束在一定范围内,减小模型复杂度;同时,如果将w约束在一定范围内,也能够有效防止梯度爆炸。
L2 Regularization = weight decay(权值衰减)
第一个wi+1为未加正则项的权重计算方式
第二个wi+1加入正则项之后的权重计算方式,化简后的公式如下,wi的系数小于1,实现了权重的衰减
Pytorch中的 weight decay 是在优化器中实现的,在优化器中加入参数weight_decay即可,参数中的weight_decay等价于正则化系数λ 。
例如下面的两个随机梯度优化器,一个是没有加入正则项,一个加入了正则项,区别仅仅在于是否设置了参数weight_decay的值:
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)
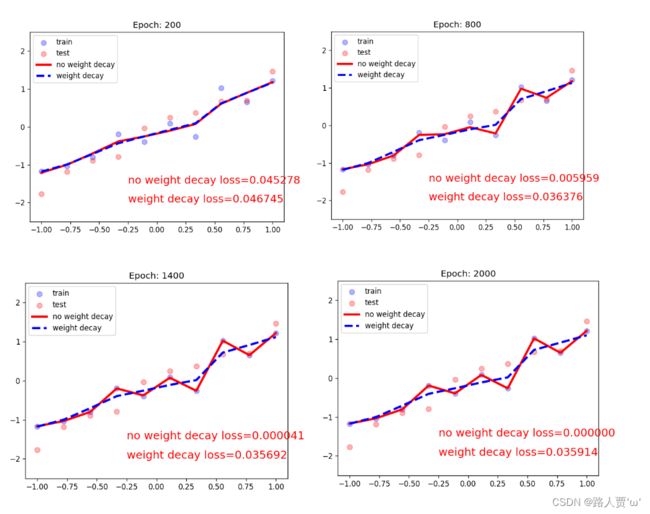
我们来看看输出结果:
可以看到,模型迭代1000次后,红线的loss基本为0,而蓝线的loss是0.035左右,虽然红线的loss很低,但是它产生了过拟合现象。
二、正则化之Dropout
2.1 Dropout概念
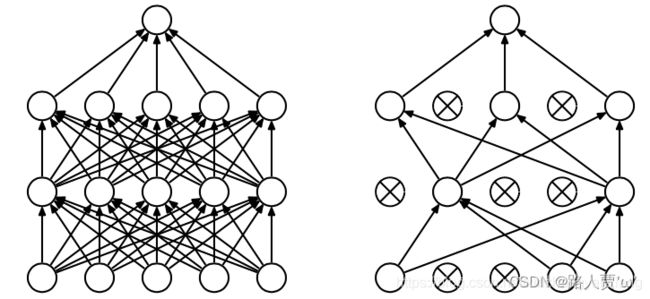
Dropout(随机失活):正常神经网络需要对每一个节点进行学习,而添加了Dropout的神经网络通过删除部分单元(随机),即暂时将其从网络中移除,以及它的所有传入和传出连接。将Dropout应用于神经网络相当于从神经网络中采样了一个“更薄的”网络,即单元个数较少。如下图所示,Dropout是从左图采样了一个更薄的网络,如图右
我们有时候之所以会出现过拟合现象,就是因为我们的网络太复杂了,参数太多了,并且我们后面层的网络也可能太过于依赖前层的某个神经元,加入Dropout之后, 首先网络会变得简单,减少一些参数,并且由于不知道浅层的哪些神经元会失活,导致后面的网络不敢放太多的权重在前层的某个神经元,这样就减轻了一个过渡依赖的现象, 对特征少了依赖, 从而有利于缓解过拟合。
注意事项:
数据尺度变化:只在训练的时候开启Dropout,而测试的时候是不用Dropout的,也就是说模型训练的时候会随机失活一部分神经元, 而测试的时候我们用所有的神经元,那么这时候就会出现这个数据尺度的问题,首先介绍一下,drop_prob就是随机失活概率。
实现细节:
- 训练时,所有权重乘以1/(1-p),即除以1-p
- 测试时,所有权重乘以1-drop_prob,drop_prob = 0.3,1-drop_prob = 0.7
2.2 nn.Dropout
nn.Dropout
功能:Dropout层
参数:
- p:被舍弃概率,失活概率
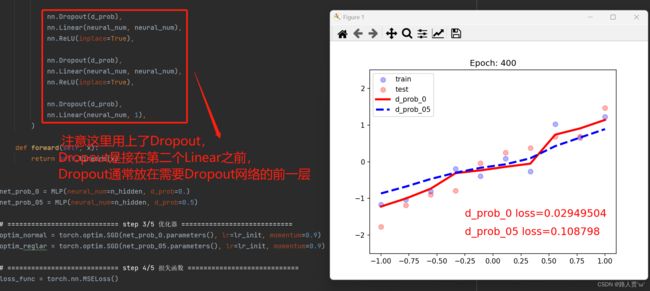
代码及输出结果:
红色曲线出现了过拟合
蓝色曲线没有过拟合
Dropout实现了类似L2的权重衰减的功能
三、归一化之Batch Normalization(BN层)
3.1 Batch Normalization介绍
Batch Normalization,简称BN,是google团队在2015年论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》提出的。这是一个神经网络训练的技巧,它不仅可以加快了模型的收敛速度,而且更重要的是在一定程度缓解了深层网络中“梯度弥散(特征分布较散)”的问题,从而使得训练深层网络模型更加容易和稳定。所以目前BN已经成为几乎所有卷积神经网络的标配技巧了。
从字面意思看来Batch Normalization就是对每一批数据进行归一化,确实如此,对于训练中某一个batch的数据{x1,x2,…,xn},注意这个数据是可以输入也可以是网络中间的某一层输出。在BN出现之前,我们的归一化操作一般都在数据输入层,对输入的数据进行求均值以及求方差做归一化,但是BN的出现打破了这一个规定,我们可以在网络中任意一层进行归一化处理,因为我们现在所用的优化方法大多都是min-batch SGD,所以我们的归一化操作就称为Batch Normalization。
为什么加了BN之后就不用精心设计权值初始化了呢?
我们来看看代码:
from tools.common_tools import set_seed
set_seed(1) # 设置随机种子
class MLP(nn.Module):
def __init__(self, neural_num, layers=100):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.bns = nn.ModuleList([nn.BatchNorm1d(neural_num) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear), bn in zip(enumerate(self.linears), self.bns):
x = linear(x)
# x = bn(x)
x = torch.relu(x)
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
print("layers:{}, std:{}".format(i, x.std().item()))
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
# method 1
nn.init.normal_(m.weight.data, std=1) # normal: mean=0, std=1
# method 2 kaiming
# nn.init.kaiming_normal_(m.weight.data)
neural_nums = 256
layer_nums = 100
batch_size = 16
net = MLP(neural_nums, layer_nums)
# net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
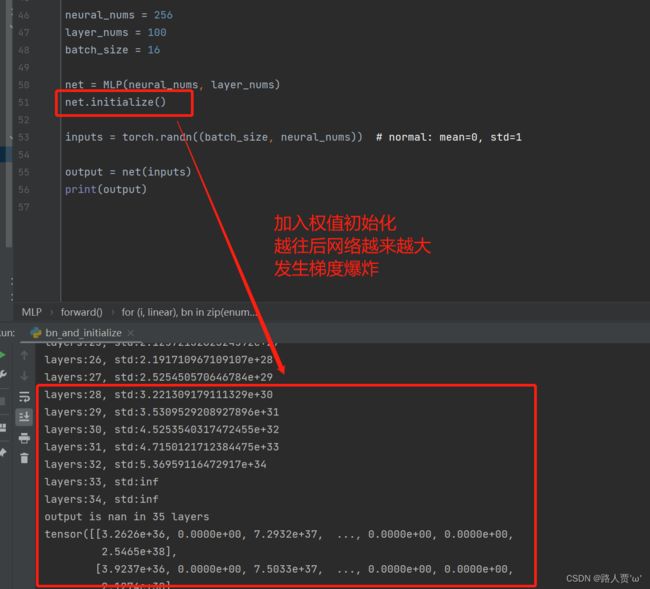
output = net(inputs)
print(output)输出结果:
不进行权值初始化,导致梯度消失
接下来,我们进行权值初始化来观察一下梯度的变化情况
代码:
net.initialize()输出结果:
采用标准正态分布的初始化方法,可以发现发生了梯度爆炸
因为此时用到的激活函数是RELU,所以使用kaiming初始化方法
代码:
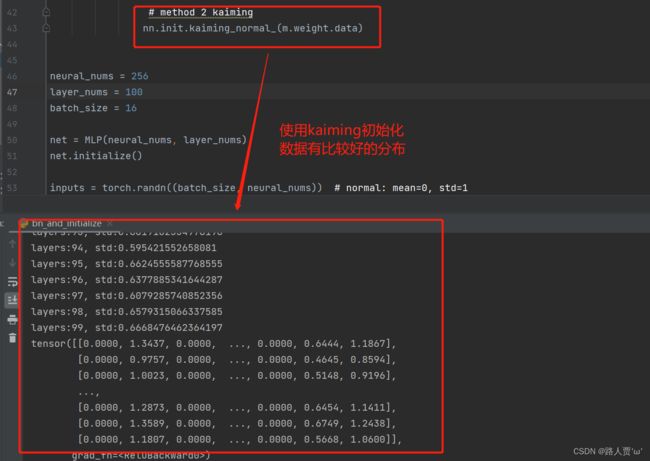
# method 2 kaiming
nn.init.kaiming_normal_(m.weight.data)输出结果:
梯度在0.6左右
以上使我们第六节讲的内容(Pytorch学习笔记(6):模型的权值初始化与损失函数)刚才我们按照权值初始化的方法来防止梯度爆炸,在这中间,考虑到relu,我们就得用Kaiming初始化,考虑到tanh,我们还得用Xavier, 这样就相当麻烦了。
那么我们假设不用权值初始化,而是在网络层的激活函数前加上BN呢?
代码:
x = bn(x)输出结果:
可以发现,BN依然可以保证数据的尺度,并且好处就是我们不用再考虑用什么样的方式进行权值的初始化。
3.2 Pytorch的Batch Normalization 1d/2d/3d实现
Pytorch中提供了三种BatchNorm方法:
- nn.BatchNorm1d
- nn.BatchNorm2d
- nn.BatchNorm3d
上面三个BatchNorm方法都继承_BatchNorm类
参数:
- num_features:一个样本特征维度(通道数)
- eps:分母修正项,为数值稳定性而加到分母上的值,一般设置比较小的数:1e的-5次方,防止除以0导致错误
- momentum:移动平均的动量值(通常设置为0.1)
- affine:是否需要affine transform(布尔变量,控制是否需要进行Affine,默认为打开)
- track_running_states:是训练状态,还是测试状态。(如果在训练状态,均值、方差需要重新估计;如果在测试状态,会采用当前的统计信息,均值、方差固定的,但训练时这两个数据是会根据batch发生改变。)
这里其他几个参数都不重要,只需要看num_features就可以了。num_features就是你需要归一化的那一维的维度。
BatchNorm的三个方法也是有属性的:
- running_mean: 均值
- running_var: 方差
- weight: affine transform中的γ
- bias: affine transforom中的β
接下来,我们详细介绍一下这三个方法。
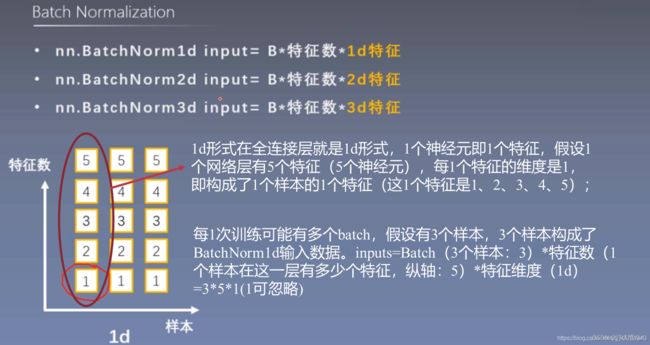
(1)nn.BatchNorm1d input = B * 特征数 * 1d特征
nn.BatchNorm1d本身不是给定输入矩阵,输出归一化结果的函数,而是定义了一个方法,再用这个方法去做归一化。
代码:
# ========nn.BatchNorm1d======== #
# 输入和输出的尺度是一样的
m = nn.BatchNorm1d(2)
m1 = nn.BatchNorm1d(2,affine=False)
input = torch.randn(2,2)
output = m(input)
output1 = m1(input)
print(output,output1)
print(output.shape,output1.shape)(2)nn.BatchNorm1d input = B * 特征数 * 2d特征
通常,卷积神经网络输出的特征图就是2d形式。
代码:
# ========nn.BatchNorm2d======== #
# 输入和输出的形状是一样的:[N,C,H,W] => [N,C,H,W]
# 因为Batch Normalization是在通道 C维度上计算统计量,因此也称为Spatial Batch Normalization
m = nn.BatchNorm2d(2, affine=False)
input = torch.randn(2,2,3,3)
output = m(input)
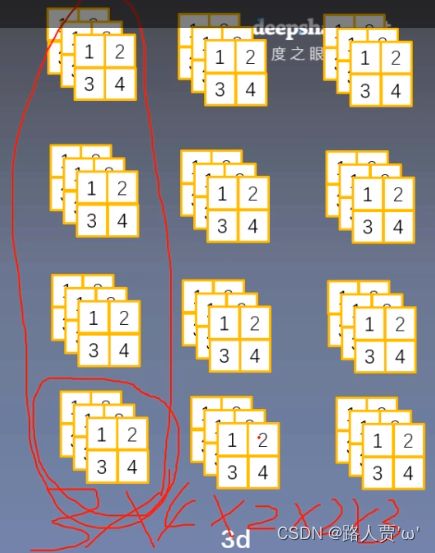
print(output)(3)nn.BatchNorm1d input = B * 特征数 * 3d特征
这个在时空序列中会用到。
代码:
# ========nn.BatchNorm3d======== #
# [N, C, D, H, W] 输入等于输出
m = nn.BatchNorm3d(100)
input = torch.randn(20,100,35,45,10)
output = m(input)
print(output.shape)四、归一化之Normalization_layers
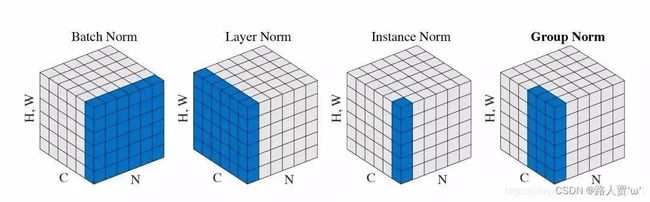
常见的Normalization
首先,我们来介绍一下深度网络中的数据维度。深度网络中的数据维度一般是( N , C , H , W ) 或者( N , H , W , C ) 格式,N 是batch size,H / W是feature的高/宽,C是feature的channel。
- Batch Normalization(BN):取不同样本的同一个通道的特征做归一化,逐特征维度归一化。这个就是对batch维度进行计算。所以假设5个100通道的特征图的话,就会计算出100个均值方差。5个batch中每一个通道就会计算出来一个均值方差。
- Layer Normalization(LN):取的是同一个样本的不同通道做归一化,逐个样本归一化。5个10通道的特征图,LN会给出5个均值方差。
- Instance Normalization(IN):仅仅对每一个图片的每一个通道做归一化,逐个通道归一化。也就是说,对【H,W】维度做归一化。假设一个特征图有10个通道,那么就会得到10个均值和10个方差;要是一个batch有5个样本,每个样本有10个通道,那么IN总共会计算出50个均值方差。
- Group Normalization(GN):这个是介于LN和IN之间的一种方法。假设Group分成2个,那么10个通道就会被分成5和5两组。然后5个10通道特征图会计算出10个均值方差。
我们来用表格进行一下对比:
| 名称 | 操作维度 | 优点 | 缺点 | 适用情况 |
|---|---|---|---|---|
| BN | (N,H,W) | 减轻对初始值的依赖,提高网络的训练效率。可以使用更高色学习速率 | 依赖Batch的大小,当Batch太小计算的均值和方差不稳定 | 深度固定的CNN/DNN等神经网络 |
| LN | (C,H,W) | 抛弃对Batch大小的依赖 | 由于其根据不同的通道进行了归一化,因此对相似度较大的特征LN会降低模型的表达能力 | mini_Batch较小的场景、动态网络结构、RNN |
| IN | (H,W) | 对于样式转换任务,IN在丢弃图像对比度信息方面优于BN | IN还可以看作是将LN单独应用于每个通道,就像通道的数量为1的LN一样,其大部分实际用效果较差 | 风格化类的图像应用 |
| GN | LN与IN的中间体 | 由于GN可利用跨通道的依赖关系因此其优于IN;因为它允许对每一组通道学习不同的分布所以它也比LN好;当批大小较小时,GN始终优于BN | 当批处理大小非常大时,GN的伸缩性不如BN,可能无法匹配BN的性能 | Batch较小(本人实验batch的大小小于10可使用GN) |
4.1Layer Normalization(LN)
起因:BN不适用于变长的网络,如RNN(网络神经元长度不一样)
思路:逐层计算均值和方差(在相同样本中计算均值和方差)
注意事项:
- 不再有running_mean和running_var
- gamma和beta为逐元素;BN中的gamma和beta的维度为特征个数
对于该变长网络,如果进行BN,只能计算前三个均值和方差,再多计算就会因为神经元得缺失而出现偏差。
nn.LayerNorm
主要参数:
- normalized_shape:该层特征形状
- eps:分母修正项,为数值稳定性而加到分母上的值,一般设置比较小的数:1e的-5次方,防止除以0导致错误
- elementwise affine:是否需要affine transform(布尔变量,控制是否需要进行Affine,默认为打开)
注意:当输入是卷积的特征图,则求平均数的数据为channelHW;
代码:
# ================nn.layer norm=================== #
batch_size = 2
num_features = 3 # 每个数据的特征个数
features_shape = (2, 2) # 特征维度
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
# feature_maps_bs shape is [8, 6, 3, 4], B * C * H * W
ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True) # LN不需要将batch_size传入
# ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=False) # 注意elementwise_affine的具体作用,elementwise_affine的作用是不适用affine transform
# ln = nn.LayerNorm([6, 3, 4])
# ln = nn.LayerNorm([6, 3])
output = ln(feature_maps_bs)
print("Layer Normalization")
print(ln.weight.shape) # 维度为[6,3,4]
print(feature_maps_bs[0, ...])
print(output[0, ...])输出结果:
(图片来源:翻滚的小@强)
4. 2Instance Normalization(IN)
起因:BN在图像生成(Image Generation)中不适用
思路:逐Instance(channel)计算均值和方差
图像生成中,一个batch不同图像有不同的迁移风格,所以不能对图片的batch进行BN,所以提出了逐通道的IN。
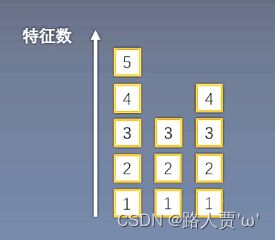
下面通过一个示意图分析IN的具体作用,如果现在有三个样本,每个样本有三个特征图,每个特征图的大小为2*2,因为每个样本代表的风格是不同的,不能将batch_size大小的图片进行BN。
IN通过逐通道(每个特征图)计算均值和方差,如上图中,第一个样本有三个特征图,在每一个特征图中计算均值和方差。
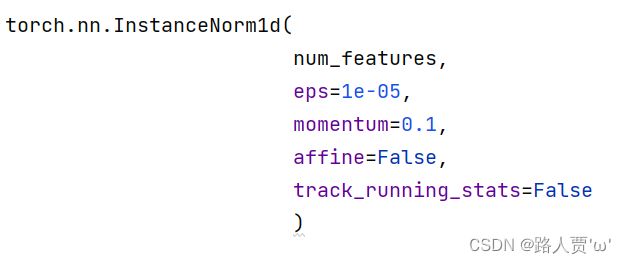
nn.InstanceNorm
主要参数:
- num_features:一个样本特征维度(通道数)
- eps:分母修正项,为数值稳定性而加到分母上的值,一般设置比较小的数:1e的-5次方,防止除以0导致错误
- momentum:移动平均的动量值(通常设置为0.1)
- affine:是否需要affine transform(布尔变量,控制是否需要进行Affine,默认为打开)
- track_running_stats:是训练状态,还是测试状态。(如果在训练状态,均值、方差需要重新估计;如果在测试状态,会采用当前的统计信息,均值、方差固定的,但训练时这两个数据是会根据batch发生改变。)
代码:
nn.InstanceNorm的使用和BN差不多,同样有nn.InstanceNorm1d,nn.InstanceNorm2d,nn.InstanceNorm3d,其使用方法和BN使用方法差不多
# =================== nn.instance norm 2d===================== #
batch_size = 3
num_features = 3
momentum = 0.3
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
print("Instance Normalization")
print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))
instance_n = nn.InstanceNorm2d(num_features=num_features, momentum=momentum)
for i in range(1):
outputs = instance_n(feature_maps_bs)
print(outputs)
# print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape))
# print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape))
# print("iter:{}, weight.shape: {}".format(i, bn.weight.shape))
# print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))输出结果:因为IN是基于通道计算均值和方差,因此得到的output的均值和方差为零。
(图片来源:翻滚的小@强)
4.3 Group Normalization(GN)
起因:小batch样本中,BN估计的均值和方差不准确;
思路:数据不够,通道来凑;
注意事项:
- 不再有running_mean和running_var;
- gamma和beta为逐通道(channel);
应用场景:大模型(小batch size)任务;大模型任务占据很大的内存,batch_size只能很小。
如图,batch_size非常少,如果用BN,因为batch_size非常小导致估计的均值和方差不准确,会导致BN失效。GN会在通道上进行分组,再基于分组后得到的数据计算均值和方差。
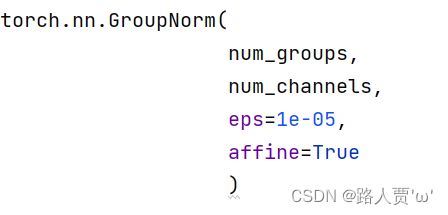
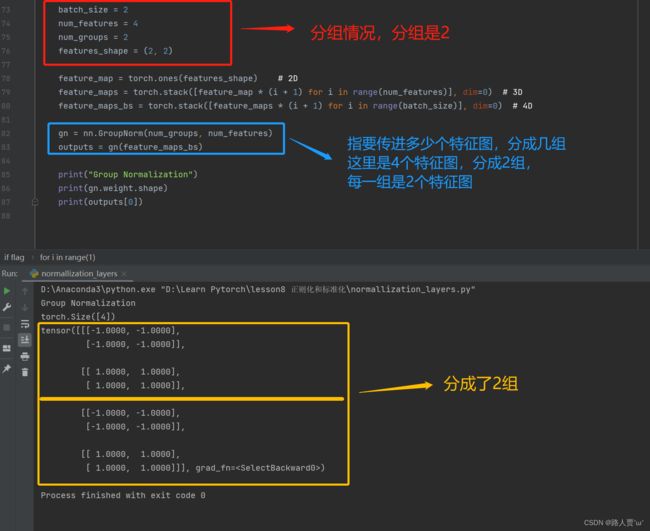
nn.GroupNorm
主要参数:
- num_groups:分组数,通常为2的n次方;
- num_channels:通道数(特征数);
- eps:分母修正项,为数值稳定性而加到分母上的值,一般设置比较小的数:1e的-5次方,防止除以0导致错误
- affine:是否需要affine transform(布尔变量,控制是否需要进行Affine,默认为打开)
代码:
# =============== nn.grop norm======================= #
batch_size = 2
num_features = 4
num_groups = 4 # 3 Expected number of channels in input to be divisible by num_groups
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0) # 4D
gn = nn.GroupNorm(num_groups, num_features)
outputs = gn(feature_maps_bs)
print("Group Normalization")
print(gn.weight.shape)
print(outputs[0])输出:
本文参考:
[PyTorch 学习笔记] 6.2 Normalization - 知乎 (zhihu.com)
系统学习Pytorch笔记九:正则化与标准化大总结