40、NeRF in the Dark

简介

主页：https://bmild.github.io/rawnerf/index.html

知识点补充：rawRGB与RGB

rawRGB

图像采集的过程为：光照在成像物体被反射 -> 镜头汇聚 -> Sensor光电转换-> ADC转换为rawRGB

因为sensor上每个像素只采集特定颜色的光的强度，因此sensor每个像素只能为R或G或B，形成的数据就成为了rawRGB数据。

rawRGB数据是sensor的经过光电转换后通过ADC采样后直接输出数据，是未经处理过的数据，表示sensor接受到的各种光的强度。

对于不同的sensor，在其内部形成的rawRGB数据格式也是有区别的。rawRGB数据排列格式有四种如下表（这里的格式是对于2*2像素矩阵而言的）：

假设一个sensor的像素是88（分辨率为88），那么这个sensor就有8*8个感光点，每个感光点就是一个晶体管。那么对于上表中四种排列格式的rawRGB数据如下图所示：

由上图可以看出，每一种格式的rawRGB数据的G分量都是B、R分量的两倍，是因为人眼对于绿色的更加敏感，所以加重了其在感光点的权重，增加了对绿色信息的采样。

RGB

在数字化的时代，需要一种标准来量化自然界的各种颜色。RGB就是一种在数字化领域表示颜色的标准，也称作一种色彩空间，通过用三原色R、G、B的不同的亮度值组合来表示某一种具体的颜色。注意，RGB里面存的是颜色的亮度值，而不是色度值。

在实际应用中，RGB存在着许多的格式，之所以存在着这些格式，是因为随着技术的进步，系统的更迭，不同的应用场景和设备环境，对颜色表达的需求是不同的。

常用的RGB格式如下表所示

rawRGB to RGB

RAW格式的主要优点是节省传输带宽，降低硬件成本，对相机、摄像机产品的大规模普及起到了极为重要的推动作用。在相机、摄像机产品中一般会使用专用的ISP硬件负责颜色插值，以支持海量数据的高速实时处理。现在也有越来越多的摄影爱好者和专业影视从业者倾向于前期只录制RAW格式文件，后期用电脑软件进行编辑制作

对RAW数据进行插值的过程叫做Bayer demosaicking，其原理如下图所示

天下没有免费的午餐，RAW格式省带宽省成本的代价是丢弃了2/3的数据量。就像人死不能复生一样，数据一旦被丢弃就再也没人知道它们到底是多少——但是人们还可以猜，图像信号一般都会存在大量的冗余，相邻像素间的差异一般不大，所以很多时候人们都能猜个八九不离十。这个过程在数学上叫做插值（interpolation），就是根据已知的数据去推测未知的数据

论文介绍

通过联合优化多个输入图像的单一场景表示，NeRF对高水平的图像噪声具有惊人的鲁棒性。利用这一事实直接在完全未处理的HDR线性原始图像上训练RawNeRF。在这个只点燃一根蜡烛的夜间场景中(a)， RawNeRF可以从嘈杂的原始数据中提取细节，这些数据会被后处理破坏(b, c)。RawNeRF恢复完整的HDR颜色信息，使HDR视图合成任务，如改变焦点和曝光，以呈现新的视图。最终的渲染图可以像任何原始照片一样进行修饰:这里展示了(d，左)一个用简单的全局色调映射的深色全焦曝光，(d，右)一个用HDRNet后处理的更亮的综合重聚焦曝光

从raw到RGB，经过标准的相机后处理管道(例如，HDR+)破坏了原始数据的简单噪声分布，引入了显著的偏差，以减少方差并产生可接受的输出图像，将这些图像输入NeRF将产生带有不正确颜色的有偏差的重建，特别是在场景的最黑暗区域，NeRF in the Dark 研究直接利用raw格式图片重建高质量3D场景

贡献点

1. 提出了一种直接在原始图像上训练RawNeRF的方法，该方法可以处理高动态范围的场景以及在黑暗中捕获的噪声输入
2. RawNeRF在有噪声的真实数据集和合成数据集上优于NeRF，对于宽基线静态场景是一种有竞争力的多图像去噪方法
3. 展示了通过线性HDR场景表示(不同曝光、色调映射和焦点)实现的新颖的视图合成应用。

Noisy Raw Input Data

NeRF以后期处理的低动态范围(LDR) sRGB彩色空间图像作为输入。当使用干净、无噪声、对比度最小的图像时，这种方法效果很好。然而，所有真实的图像都包含一定程度的噪声，而相机后处理管道中的每一步都以某种方式破坏了这种分布

Raw camera measurements （raw 相机测量）

当捕捉图像时，击中相机传感器像素的光子数被转换为电荷，这被记录为高位深数字信号(通常为10到14位)。这些值被一个“黑电平”抵消，以允许由于噪声而产生负测量值。经过黑电平减法后，信号是一个有噪声的量 y_i ，其量 x_i 与快门打开时预期到达的光子数成比例。这种噪声来自两个物理事实，即光子到达是泊松过程( “shot” noise ) 和 readout 电路中的噪声，后者将模拟电信号转换为数字值 (“read” noise) 。shot 和 read noise 的组合分布可以很好地建模为高斯分布，其方差是其均值的仿射函数;重要的是，这意味着误差 y_i−x_i 的分布是零均值。

Color filter demosaicking（彩色滤镜马赛克）

摄像机在图像传感器前包含一个拜耳滤色器阵列，这样每个像素的光谱响应曲线可以测量红光、绿光或蓝光。像素颜色值通常排列在 2 × 2 的正方形中，其中包含两个绿色像素、一个红色像素和一个蓝色像素(称为拜耳模式)，从而产生“马赛克”数据。为了生成一幅全分辨率的彩色图像，利用镶嵌算法对缺失的彩色通道进行插值。这种插值在空间上与噪声相关，马赛克的棋盘式模式在交替像素中导致不同的噪声水平。
| R | G |
| G | B |

Color correction and white balance（色彩校正和白平衡）

每个彩色滤光片元素的光谱响应曲线在不同的相机之间是不同的，并使用一个颜色校正矩阵将图像从这个相机特定的颜色空间转换为一个标准化的颜色空间。此外，由于人类对不同光源所赋予的色彩的感知是稳定的，照相机试图通过估计的白平衡系数缩放每个颜色通道来解释这种色彩(即，使白色表面看起来像rgb中性白色)。这两个步骤通常结合成一个线性3 × 3矩阵变换，进一步关联颜色通道之间的噪声。

Gamma compression and tonemapping （伽马压缩和色调映射）

人类能够分辨出图像中黑暗区域与明亮区域之间较小的相对差异。sRGB伽马压缩利用了这一事实，它通过裁剪[0,1]外的值并对信号应用非线性曲线来优化最终的图像编码，以压缩明亮的亮点为代价，将更多的比特用于黑暗区域。除了伽马压缩，当图像被量化为8比特时，色调映射算法可以用来更好地保持高动态范围场景(明亮区域比最暗区域亮几个数量级)的对比度。

这两个步骤联合称为“tonemapping”，表示将线性HDR值映射到非线性LDR空间以进行可视化的过程。将tonmapping之前的信号称为高动态范围(HDR)，之后的信号称为低动态范围(LDR)。在所有的后处理操作中，色调映射对噪声分布的影响是最剧烈的:裁剪完全丢弃了最亮和最暗区域的信息，非线性的色调映射曲线后，噪声不再保证为高斯甚至零均值。

RawNeRF

将原始HDR图像转换为LDR图像有两个重要后果

1. 明亮区域的细节丢失，当值从上面裁剪为1时，图像的细节被色调映射曲线压缩，随后量化为8比特
2. 每像素的噪声分布在经过非线性色调映射曲线并从下方在零处裁剪后变得有偏差(不再是零均值)。

RawNeRF的目标是利用这些信息，而不是丢弃它，直接在HDR颜色空间的线性原始输入数据上优化NeRF。在原始空间中重构NeRF使其对噪声输入更稳健，并允许新的HDR视图合成应用。

标准的NeRF训练管道(a)接收通过相机处理管道发送的LDR图像，重建场景并在LDR颜色空间中呈现新的视图。因此，它的渲染已经有效地进行了后期处理，不能明显地修饰。相反，RawNeRF (b)修改了NeRF，以直接在线性原始HDR输入数据上训练。由此产生的场景再现产生了新的观点，可以像任何原始照片一样编辑。

Loss function

由于HDR图像的颜色分布可以跨越多个数量级，在HDR空间中应用的标准L2损耗将完全被明亮区域的错误所主导，并在色调映射时产生具有低对比度的浑浊黑暗区域的图像

(a)在其第 90^th 和第 10^th 个原始颜色百分比之间有一个 7000× 的比例。(b)当面对这样的高对比度输入时，标准的L2损失从NeRF成功地恢复了场景的明亮部分，但在较暗的区域产生了较差的结果，这在LDR色调映射后变得特别明显。（c）论文提出的损失，根据对数色调图曲线的梯度重新加权，成功地重建了场景的所有部分。两个渲染的图像都是使用**HDR+**进行调色的。

采用更强烈地惩罚黑暗区域错误的损失，以与人类感知压缩动态范围的方式相一致。实现这一目标的一种方法是在应用损失函数之前，通过色调映射曲线 ψ 传递渲染后的估计 $\hat{y}$ 和观测到的噪声强度 y

然而，在微光原始图像中，观测到的信号y被零均值噪声严重破坏，非线性色调映射会引入偏差，从而改变噪声信号的期望值 ( E[ψ(y)] $\ne$ ψ(E[y]) ) 。为了使网络收敛到无偏结果，改用加权L2损失形式

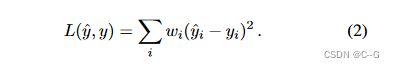
可以通过线性化每一个 ${\hat{y}}_i$ 周围的色调曲线ψ来近似这种形式的色调映射损失(1):

**sg(·)**表示停止梯度，将其参数视为零导数的常数，防止其在反向传播过程中影响损失梯度

在 $ϵ=10^{-3}$ 的“梯度监督”色调曲线 $\psi (z)=log(y+ϵ)$ 产生了感知高质量的结果，且误差极小，这意味着损失权重项 $\psi \prime (sg({\hat{y}}_i))=(sg({\hat{y}}_i)+ϵ{)}^{-1}$ 和最终损失

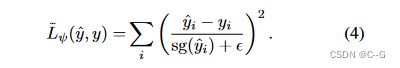
这正好对应于在Noise2Noise中训练有噪声的HDR路径跟踪数据时用于获得无偏倚结果的相对MSE损失。ψ曲线与音频处理中用于范围压缩的μ-law函数成比例，以前用作音调映射函数，监督网络将LDR图像映射到HDR输出

Variable exposure training

在具有非常高动态范围的场景中，即使是10-14位的原始图像也可能不足以在一次曝光中同时捕捉亮区和暗区,许多数码相机都采用了“包围”模式，在这种模式下，不同快门速度的多张照片在瞬间被捕捉到，然后将其合并，以利用曝光时间较短时保留的明亮亮点，以及曝光时间较短时捕捉到的细节较多的黑暗区域

在亮度变化极大的场景中，固定的快门速度不足以捕捉到完整的动态范围。(a)例如，这个场景需要不同的曝光捕捉，以避免在黑暗的室内区域或吹散的天空高光的质量差。只有经过短曝光和长曝光优化的RawNeRF模型才能恢复完整的动态范围。(b)这种亮度变化太大，无法在单一图像中使用简单的全局sRGB伽马曲线进行可视化，需要更复杂的局部色调映射算法(例如，HDR+后处理)。

RawNeRF可使用可变曝光

给定一组曝光时间为 $t_i$ 的图像 I_i (其他所有捕获参数保持不变)，可以通过按记录的快门速度 t_i 缩放RawNeRF的线性空间颜色输出，使其与图像 I_i 中的亮度匹配。

由于传感器的错误校准，不同的曝光不能精确地使用快门速度单独对齐，为此，为捕获的图像集中的每个独特快门速度添加了一个学习的每颜色通道缩放因子，与NeRF网络联合优化。

最终RawNeRF“曝光”给定输出颜色 $\widehat{y_i}$ 从网络然后 $min(\widehat{y_i^c}\cdot t_i\cdot {\alpha }_{t_i}^c,1)$，其中 c 索引颜色通道，${\alpha }_{t_i}^c$ 是学习到的快门速度 t_i 和通道 c 的比例因子(我们约束 $a_{t_{max}}^c=1$ 的最长曝光)。我们从上面剪辑 1，以说明像素饱和在过度曝光的区域。这个比例和剪切值传递给前面描述的损失

Implementation details

论文网络模型基于mip-NeRF，唯一的网络架构更改是修改MLP的输出颜色的激活函数从一个 sigmoid 到一个指数函数，以更好地参数化线性亮度值，使用Adam优化器，在所有训练图像中采样16k随机射线批次，在500k的优化步骤中，学习率从10⁻³衰减到10⁻⁵。

极度嘈杂的场景受益于对体积密度的正则化损失，以防止部分透明的“浮子”伪影。在体绘制过程中，对沿着光线累积颜色值的权重分布的方差进行了损失

原始输入数据是镶嵌的，每个像素只包含一个颜色值，只将损失应用到每个像素的活动颜色通道，这样优化NeRF有效地马赛克输入图像。任何重采样步骤都会影响原始噪声分布，所以不会对输入进行失真或下采样，而是使用全分辨率的马赛克图像(场景通常为12MP)进行训练，为此，使用相机固有的考虑径向失真时产生的射线，COLMAP不支持原始图像，因此使用全分辨率的后处理JPEG图像来计算相机姿态

效果

补充

损失函数

希望用以下损失来近似训练的效果

需要收敛到一个无偏的结果。这可以通过对误差项使用局部有效的线性逼近来完成

选择围绕${\hat{y}}_i$进行线性化是因为，与嘈杂的观察 y_i 不同，${\hat{y}}_i$在训练过程中倾向于真实的信号值 x_i = E[y_i]

如果使用加权L2损失，那么当我们训练网络时，我们将得到${\hat{y}}_i\to E[y_i]=x_i$的期望(其中 x_i 是真实的信号值)。这意味着这些条款加起来就是梯度加权损失

重新加权损失 7 的梯度是色调映射损失 5 的梯度的线性近似

在第10行，替换了第6行的线性化，在第11行，利用了一个事实，即停止梯度对不会进一步微分的表达式没有影响

权重方差正则化器是一个合成权重的函数，用于计算每条射线的最终颜色。给定长度为 ∆_i 的各射线段 [t_i−1,t_i) 的MLP输出 c_i， σ_i，这些权值为

如果使用这些权重定义射线段上的分段常数概率分布 p_w，那么方差正则化器等于

计算平均值(期望深度)

将此值记为 $\bar{t}$

对 L_w 应用 1 × 10⁻²到 1 × 10⁻¹之间的权重(相对于渲染损失)，通常在噪音较大或较暗的场景中使用更高的权重，这些场景更容易出现“漂浮”伪影。使用这种高重量的正则化剂可以导致轻微的锐度损失，可以通过在训练过程中将其重量从 0 退火到 1 来改善

在实践中，直接通过所需色调曲线的导数来缩放损失

对 $ϵ$ 和 p 执行了形式 $(sg({\hat{y}}_i)+ϵ{)}^{-p}$ 的损失权重的超参数扫描，发现 $ϵ=1\times 10^{-3}$ 和 p = 1产生了最好的定性结果