CTR 预测理论（十七）：回归和分类损失函数总结

损失函数作为建模的一个重要环节，一个针对模型、数据集都合适的损失函数对于建模的好坏至关重要，现查询相关资料，将常见的分类、回归损失函数及常用的 Tensorflow 代码总结于此，仅用于学习交流。

常见回归和分类损失函数比较

损失函数的定义为 $L(y,f(x))$，衡量真实值 $y$ 和预测值 $f(x)$ 之间不一致的程度，一般越小越好。为了便于不同损失函数的比较，常将其表示为单变量的函数，在回归问题中这个变量为 $y-f(x)$，在分类问题中则为 $yf(x)$。

下面分别进行讨论。

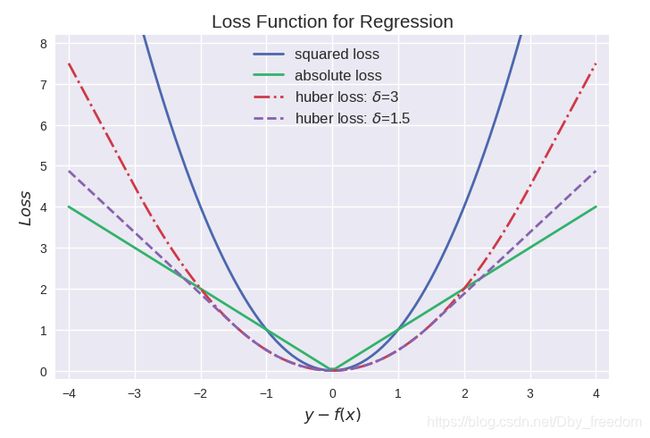
1. 回归问题的损失函数

回归问题中 $y$ 和 $f(x)$ 皆为实数 $\in R$，因此用残差 $y-f(x)$ 来度量二者的不一致程度。残差（的绝对值）越大，则损失函数越大，学习出来的模型效果就越差（这里不考虑正则化问题）。

常见的回归损失函数有：

• 平方损失 (squared loss) ： $(y-f(x){)}^2$
• 绝对值 (absolute loss) : $|y-f(x)|$
• Huber损失 (huber loss) : $\{\begin{array}{cc}\frac{1}{2}[y-f(x){]}^2& |y-f(x)|\le \delta \\ \delta |y-f(x)|-\frac{1}{2}{\delta }^2& |y-f(x)|>\delta \end{array}$

其中最常用的是平方损失，然而其缺点是对于异常点会施以较大的惩罚，因而不够robust。

如果有较多异常点，则绝对值损失表现较好，但绝对值损失的缺点是在 $y-f(x)=0$ 处不连续可导，因而不容易优化。

Huber损失是对二者的综合，当 $|y-f(x)|$ 小于一个事先指定的值 $\delta$ 时，变为平方损失，大于 $\delta$ 时，则变成类似于绝对值损失，因此也是比较robust的损失函数。

1.1 tf.losses.mean_squared_error：均方根误差（MSE） —— 回归问题中最常用的损失函数

优点：便于梯度下降，误差大时下降快，误差小时下降慢，有利于函数收敛。
缺点：受明显偏离正常范围的离群样本的影响较大

# Tensorflow中集成的函数
mse = tf.losses.mean_squared_error(y_true, y_pred)

# 利用Tensorflow基础函数手工实现
mse = tf.reduce_mean(tf.square(y_true -  y_pred))

1.2 tf.losses.absolute_difference：平均绝对误差（MAE） —— 想格外增强对离群样本的健壮性时使用

优点：克服了 MSE 的缺点，受偏离正常范围的离群样本影响较小。
缺点：收敛速度比 MSE 慢，因为当误差大或小时其都保持同等速度下降，而且在某一点处还不可导，计算机求导比较困难。

maes = tf.losses.absolute_difference(y_true, y_pred)
maes_loss = tf.reduce_sum(maes)

1.3 tf.losses.huber_loss：Huber loss —— 集合 MSE 和 MAE 的优点，但是需要手动调超参数

核心思想是，检测真实值（y_true）和预测值（y_pred）之差的绝对值在超参数 δ 内时，使用 MSE 来计算 loss, 在 δ 外时使用类 MAE 计算 loss。sklearn 关于 huber 回归的文档中建议将 δ=1.35 以达到 95% 的有效性。

hubers = tf.losses.huber_loss(y_true, y_pred)
hubers_loss = tf.reduce_sum(hubers)

三者的图形比较如下：

1.2 回归损失函数优缺点对比：

2. 分类问题的损失函数

对于二分类问题，$y\in \left\{-1,+1\right\}$，损失函数常表示为关于 $yf(x)$ 的单调递减形式。

如下图：

$yf(x)$ 被称为 margin，其作用类似于回归问题中的残差 $y-f(x)$。

二分类问题中的分类规则通常为：

$sign(f(x))=\{\begin{array}{c}+1iff(x)\ge 0\\ -1iff(x)<0\end{array}$

可以看到如果 $yf(x)>0$，则样本分类正确，$yf(x)<0$ 则分类错误，而相应的分类决策边界即为 $f(x)=0$。

所以最小化损失函数也可以看作是最大化 margin 的过程，任何合格的分类损失函数都应该对 margin < 0 的样本施以较大的惩罚。

2.1 0-1损失 (zero-one loss)

$$L(y,f(x))=\{\begin{array}{c}0ifyf(x)\ge 0\\ 1ifyf(x)<0\end{array}$$

0-1 损失对每个错分类点都施以相同的惩罚，这样那些“错的离谱“ (即 $margin\to -\infty$)的点并不会收到大的关注，这在直觉上不是很合适。

另外0-1损失不连续、非凸，优化困难，因而常使用其他的代理损失函数进行优化。

2.2 Logistic loss

$$L(y,f(x))=log(1+e^{-yf(x)})$$

logistic Loss 为 Logistic Regression 中使用的损失函数，下面做一下简单证明：

Logistic Regression 中使用了 Sigmoid 函数表示预测概率：

$$g(f(x))=P(y=1|x)=\frac{1}{1+e^{-f(x)}}$$

而

$$P(y=-1|x)=1-P(y=1|x)=1-\frac{1}{1+e^{-f(x)}}=\frac{1}{1+e^{f(x)}}=g(-f(x))$$

因此利用$y\in \left\{-1,+1\right\}$，可写为$P(y|x)=\frac{1}{1+e^{-yf(x)}}$，此为一个概率模型，利用极大似然的思想：

$$max(\prod P(y|x))=max(\prod \frac{1}{1+e^{-yf(x)}})$$

两边取对数，又因为是求损失函数，则将极大转为极小：

$$max(\sum logP(y|x))=-min(\sum log(\frac{1}{1+e^{-yf(x)}}))=min(\sum log(1+e^{-yf(x)})$$

这样就得到了logistic loss。

$$L(y,f(x))=log(1+e^{-yf(x)})$$


如果定义 $t=\frac{y+1}{2}\in \left\{0,1\right\}$，则极大似然法可写为：

$$\prod (P(y=1|x){)}^t((1-P(y=1|x){)}^{1-t}$$

取对数并转为极小得：

$$\sum [-t\log P(y=1|x)-(1-t)\log (1-P(y=1|x))]$$

上式被称为交叉熵损失 (cross entropy loss)，可以看到在二分类问题中 logistic loss和交叉熵损失是等价的，二者区别只是标签 y 的定义不同。

其标准形式为：
$$l(y_i,{\hat{y}}_i)=y_{i}ln(1+e^{-{\hat{y}}_i})+(1-y_i)ln(1+e^{{\hat{y}}_i})$$

交叉熵损失函数作为二分类损失函数中最常用的损失函数，其对应的 TensorFlow 实现形式有如下几种：

2.2.1 tf.nn.sigmoid_cross_entropy_with_logits：先 sigmoid 再求交叉熵 —— 二分类问题首选

使用时，一定不要将预测值（y_pred）进行 sigmoid 处理，否则会影响训练的准确性，因为函数内部已经包含了 sigmoid 激活（若已先行 sigmoid 处理过了，则 tensorflow 提供了另外的函数） 。真实值（y_true）则要求是 One-hot 编码形式。

函数求得的结果是一组向量，是每个维度单独的交叉熵，如果想求总的交叉熵，使用 tf.reduce_sum() 相加即可；如果想求 loss ，则使用 tf.reduce_mean() 进行平均。

# Tensorflow中集成的函数
sigmoids = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=y_pred)
sigmoids_loss = tf.reduce_mean(sigmoids)

# 利用Tensorflow基础函数手工实现
y_pred_si = 1.0/(1+tf.exp(-y_pred))
sigmoids = -y_true*tf.log(y_pred_si) - (1-y_true)*tf.log(1-y_pred_si)
sigmoids_loss = tf.reduce_mean(sigmoids)

2.2.2 tf.losses.log_loss：交叉熵 —— 效果同上，预测值格式略有不同

预测值（y_pred）计算完成后，若已先行进行了 sigmoid 处理，则使用此函数求 loss ，若还没经过 sigmoid 处理，可直接使用 sigmoid_cross_entropy_with_logits。

# Tensorflow中集成的函数
logs = tf.losses.log_loss(labels=y, logits=y_pred)
logs_loss = tf.reduce_mean(logs)

# 利用Tensorflow基础函数手工实现
logs = -y_true*tf.log(y_pred) - (1-y_true)*tf.log(1-y_pred)
logs_loss = tf.reduce_mean(logs)

2.2.3 tf.nn.softmax_cross_entropy_with_logits_v2：先 softmax 再求交叉熵 —— 多分类问题首选

使用时，预测值（y_pred）同样是没有经过 softmax 处理过的值，真实值（y_true）要求是 One-hot 编码形式。

softmaxs = tf.nn.softmax_cross_entropy_with_logits_v2(labels=y, logits=y_pred)
softmaxs_loss = tf.reduce_mean(softmaxs)

v1.8之前为 tf.nn.softmax_cross_entropy_with_logits()，新函数修补了旧函数的不足，两者在使用方法上是一样的。

2.2.4 tf.nn.sparse_softmax_cross_entropy_with_logits：效果同上，真实值格式略有不同

若真实值（y_true）不是 One-hot 格式的，可以使用此函数，可省略一步转换

softmaxs_sparse = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=y_pred)
softmaxs_sparse_loss = tf.reduce_mean(softmaxs_sparse)

2.2.5 tf.nn.weighted_cross_entropy_with_logits：带权重的 sigmoid 交叉熵 —— 适用于正、负样本数量差距过大时

增加了一个权重的系数，用来平衡正、负样本差距，可在一定程度上解决差距过大时训练结果严重偏向大样本的情况。

# Tensorflow中集成的函数
sigmoids_weighted = tf.nn.weighted_cross_entropy_with_logits(targets=y, logits=y_pred, pos_weight)
sigmoids_weighted_loss = tf.reduce_mean(sigmoids_weighted)

# 利用Tensorflow基础函数手工实现
sigmoids_weighted = -y_true*tf.log(y_pred) * weight - (1-y_true)*tf.log(1-y_pred)
sigmoids_loss = tf.reduce_mean(sigmoids)

2.3 Hinge loss

$$L(y,f(x))=max(0,1-yf(x))$$

hinge loss 为 svm 中使用的损失函数，hinge loss 使得 $yf(x)>1$ 的样本损失皆为 0，由此带来了稀疏解，使得 svm 仅通过少量的支持向量就能确定最终超平面。

对应 TensorFlow 实现：

2.3.1 tf.losses.hinge_loss：hinge 损失函数 —— SVM 中使用

hing_loss 是为了求出不同类别间的“最大间隔”，此特性尤其适用于 SVM（支持向量机）。使用 SVM 做分类，与 LR（Logistic Regression 对数几率回归）相比，其优点是小样本量便有不错效果、对噪点包容性强，缺点是样本量大时效率低、有时很难找到合适的区分方法。

hings = tf.losses.hinge_loss(labels=y, logits=y_pred, weights)
hings_loss = tf.reduce_mean(hings)

2.4 指数损失(Exponential loss)

$$L(y,f(x))=e^{-yf(x)}$$

exponential loss为AdaBoost中使用的损失函数，使用exponential loss能比较方便地利用加法模型推导出AdaBoost算法 (具体推导过程可见)。然而其和squared loss一样，对异常点敏感，不够robust。

2.5 modified Huber loss

$$L(y,f(x))=\{\begin{array}{c}max(0,1-yf(x){)}^{2}ifyf(x)\ge -1\\ -4yf(x)ifyf(x)<-1\end{array}$$

modified huber loss 结合了 hinge loss 和 logistic loss 的优点，既能在 $yf(x)>1$ 时产生稀疏解提高训练效率，又能进行概率估计。另外其对于 $(yf(x)<-1)$ 样本的惩罚以线性增加，这意味着受异常点的干扰较少，比较robust。scikit-learn中的SGDClassifier同样实现了modified huber loss。

最后来张全家福：

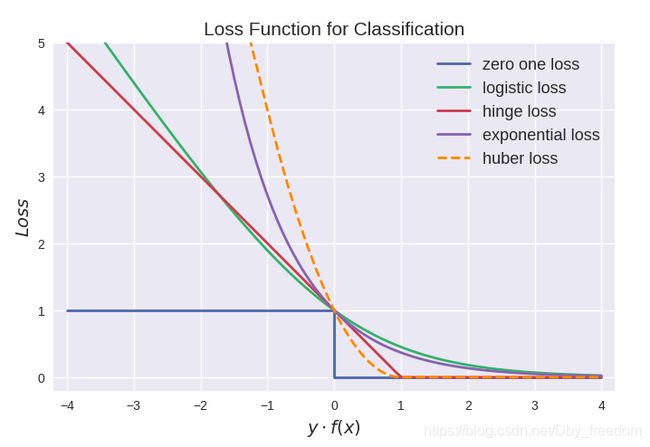
从上图可以看出上面介绍的这些损失函数都可以看作是 0-1 损失的单调连续近似函数，而因为这些损失函数通常是凸的连续函数，因此常用来代替 0-1 损失进行优化。它们的相同点是都随着 $margin\to -\infty$ 而加大惩罚；不同点在于，logistic loss 和 hinge loss 都是线性增长，而 exponential loss 是以指数增长。

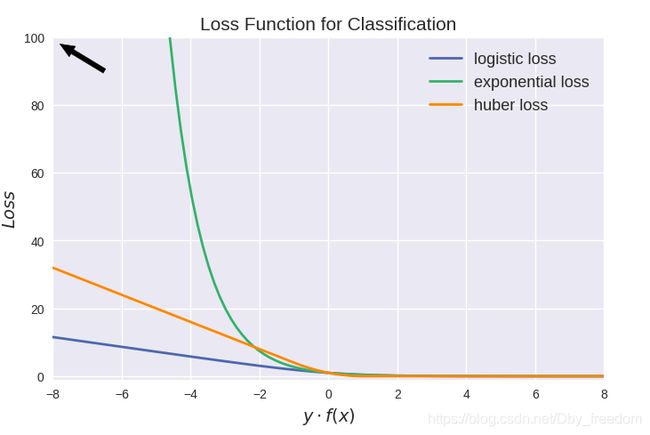
值得注意的是上图中 modified huber loss 的走向和 exponential loss 差不多，并不能看出其 robust 的属性。其实这和算法时间复杂度一样，成倍放大了之后才能体现出巨大差异：

3. Tensorflow 自定义损失函数

标准的损失函数并不合适所有场景，有些实际的背景需要采用自己构造的损失函数，Tensorflow 也提供了丰富的基础函数供自行构建。
例如下面的例子：当预测值（y_pred）比真实值（y_true）大时，使用 (y_pred-y_true)*loss_more 作为 loss，反之，使用 (y_true-y_pred)*loss_less

loss = tf.reduce_sum(tf.where(tf.greater(y_pred, y_true), (y_pred-y_true)*loss_more,(y_true-y_pred)*loss_less))

tf.greater(x, y)：判断 x 是否大于 y，当维度不一致时广播后比较
tf.where(condition, x, y)：当 condition 为 true 时返回 x，否则返回 y
tf.reduce_mean()：沿维度求平均
tf.reduce_sum()：沿维度相加
tf.reduce_prod()：沿维度相乘
tf.reduce_min()：沿维度找最小
tf.reduce_max()：沿维度找最大
使用 Tensorflow 提供的方法可自行构造想要的损失函数。

4. 参考文献

[1] 常见回归和分类损失函数比较
[2] Tensorflow 中的损失函数 —— loss 专题汇总