PCA(主成分分析)原理详解

PCA概念

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

协方差和散度矩阵

样本均值：

$$\bar{x}=\frac{1}{n}\sum _{i=1}^N{x}_i$$

样本方差：

$$S^2=\frac{1}{n-1}\sum _{i=1}^N(x_i-\bar{x}{)}^2$$

样本X和样本Y的协方差：

$$Cov(x,y)=\frac{1}{n-1}\sum _{i=1}^N(x_i-\bar{x})(y_i-\bar{y})$$

由上面的公式，我们可以得到以下结论：

1. 方差的计算公式是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征；方差是协方差的特殊情况。

2. 方差和协方差的除数是n-1,这是为了得到方差和协方差的无偏估计。

• 协方差为正时，说明X和Y是正相关关系：

• 协方差为负时，说明X和Y是负相关关系；

• 协方差为0时，说明X和Y是相互独立。

Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上是协方差矩阵(对称方阵)。例如，对于3维数据(x,y,z)，计算它的协方差就是：

散度矩阵定义为：

对于数据X的散度矩阵为$X{X}^T$。其实协方差矩阵和散度矩阵关系密切，散度矩阵 = 协方差矩阵 *（总数据量-1）。因此它们的特征值和特征向量是一样的。这里值得注意的是，散度矩阵是SVD奇异值分解的一步，因此PCA和SVD是有很大联系。

特征值分解矩阵原理

1. 特征值与特征向量

   如果一个向量v是矩阵A的特征向量，将一定可以表示成下面的形式：

   $$A\xi =\lambda \xi$$

   其中，λ是特征向量ξ应的特征值，一个矩阵的一组特征向量是一组正交向量。

2. 特征值分解矩阵

   对于矩阵A，有一组特征向量ξ，将这组向量进行正交化单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵A分解为如下式：

   $$A=QD{Q}^{-1}$$

   其中，Q是矩阵A的特征向量组成的矩阵，D则是一个对角阵，对角线上的元素就是特征值。

SVD分解矩阵原理

奇异值分解是一个能适用于任意矩阵的一种分解的方法，对于任意矩阵A总是存在一个奇异值分解：

$$A=U\sum V^T$$

假设A是一个m*n的矩阵，那么得到的U是一个mm的方阵，U里面的正交向量被称为左奇异向量。Σ是一个m\n的矩阵，Σ除了对角线其它元素都为0，对角线上的元素称为奇异值。$V^T$是v的转置矩阵，是一个n*n的矩阵，它里面的正交向量被称为右奇异值向量。而且一般来讲，我们会将Σ上的值按从大到小的顺序排列。

SVD分解矩阵A的步骤：

求$A{A}^T$的特征值和特征向量，用单位化的特征向量构成 U。

(2) 求$A{A}^T$的特征值和特征向量，用单位化的特征向量构成 V。

(3) 将$A{A}^T$或者$A{A}^T$的特征值求平方根，然后构成 Σ。

具体了解这一部分内容看《机器学习中SVD总结》文章。

PCA算法两种实现方法

基于特征值分解协方差矩阵实现PCA算法

基本步骤

输入：数据集X = {$x_1,x_2,x_3,...,x_n$}，需要降到k维

1. 去平均值(即去中心化)，即每一位特征减去各自的平均值。

2. 计算协方差矩阵$\frac{1}{n-1}X{X}^T$,注：这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。

3. 用特征值分解方法求协方差矩阵$\frac{1}{n-1}X{X}^T$的特征值与特征向量。

4. 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5. 将数据转换到k个特征向量构建的新空间中，即Y=PX。

这里用$\frac{1}{n-1}X{X}^T$来进行计算，可以求出协方差矩阵，在高纬的情况下，不能仅仅凭借方差来进行计算，就会导致方向几乎重叠，这样的维度是没有用的，让两个字段尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的。因此要增加约束条件，即协方差。协方差为0时，表示两个维度间的特征是相互独立。即使$\frac{1}{n-1}X{X}^T$相似对角化，求出的对应特征值的特征向量组成的矩阵的转置就是我们的P，这是一个正交矩阵。特征值其实代表的就是我们的方差，想降到几维，就选求几个最大的特征值对应的特征向量组成P。为什么选取最大值呢？因为特征值就是对应了我们的方差，方差越大，相应的数据的离散度就高。

更多的请看： PCA的数学原理，强烈推荐！！！

举个栗子

$$X=\left\{\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right\}$$

以X为例，我们用PCA方法将这两行数据降到一行。

1. 因为X矩阵的每行已经是零均值，所以不需要去平均值。

2. 求协方差矩阵：

   $$C=\frac{1}{5}\left\{\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right\}\left\{\begin{array}{cc}-1& -2\\ -1& 0\\ 0& 0\\ 2& 1\\ 0& 1\end{array}\right\}=\left\{\begin{array}{cc}\frac{6}{5}& \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}\end{array}\right\}$$

3. 求协方差矩阵的特征值与特征向量。

   求解后的特征值为：

   $${\lambda }_1=2,{\lambda }_2=\frac{2}{5}$$

   对应的特征向量为：

   $$c_1=\left\{\begin{array}{c}1\\ 1\end{array}\right\}{c}_2=\left\{\begin{array}{c}-1\\ 1\end{array}\right\}$$

   其中对应的特征向量分别是一个通解，$c_1$和 $c_2$可以取任意实数。那么标准化后的特征向量为：

   $$c_1=\left\{\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right\}{c}_2=\left\{\begin{array}{c}-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right\}$$

4. 矩阵P为：

   $$P=\left\{\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right\}$$

5. 最后我们用P的第一行乘以数据矩阵X，就得到了降维后的表示：

   $$X=\left\{\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right\}\left\{\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right\}=\left\{\begin{array}{ccccc}-\frac{3}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& \frac{3}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}\right\}$$

6. 结果如图1所示：

   

注意：如果我们通过特征值分解协方差矩阵，那么我们只能得到一个方向的PCA降维。这个方向就是对数据矩阵X从行(或列)方向上压缩降维。

基于SVD分解协方差矩阵实现PCA算法

输入：数据集X = {$x_1,x_2,x_3,...,x_n$}，需要降到k维

1. 去平均值(即去中心化)，即每一位特征减去各自的平均值。
2. 计算协方差矩阵。
3. 通过SVD计算协方差矩阵的特征值与特征向量。
4. 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
5. 将数据转换到k个特征向量构建的新空间中。

在PCA降维中，我们需要找到样本协方差矩阵$X{X}^T$的最大k个特征向量，然后用这最大的k个特征向量组成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$X{X}^T$,当样本数多、样本特征数也多的时候，这个计算还是很大的。当我们用到SVD分解协方差矩阵的时候，SVD有两个好处：

1. 有一些SVD的实现算法可以先不求出协方差矩阵$X{X}^T$也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解而是通过SVD来完成，这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征值分解。

2. 注意到PCA仅仅使用了我们SVD的左奇异矩阵，没有使用到右奇异值矩阵，那么右奇异值矩阵有什么用呢？假设我们的样本是m*n的矩阵X，如果我们通过SVD找到了矩阵$X{X}^T$最大的k个特征向量组成的k*n的矩阵 $V^T$,则我们可以做如下处理：

   $$X_{m\ast k}^2=X_{m\ast n}{V}_{n\ast k}^T$$

   可以得到一个m*k的矩阵X’,这个矩阵和我们原来m*n的矩阵X相比，列数从n减到了k，可见对列数进行了压缩。也就是说，左奇异矩阵可以用于对行数的压缩；右奇异矩阵可以用于对列(即特征维度)的压缩。这就是我们用SVD分解协方差矩阵实现PCA可以得到两个方向的PCA降维(即行和列两个方向)。

PCA的理论推导

PCA有两种通俗易懂的解释：(1)最大方差理论；(2)最小化降维造成的损失。这两个思路都能推导出同样的结果。

我在这里只介绍最大方差理论：

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。样本在u1上的投影方差较大，在u2上的投影方差较小，那么可认为u2上的投影是由噪声引起的。

因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。

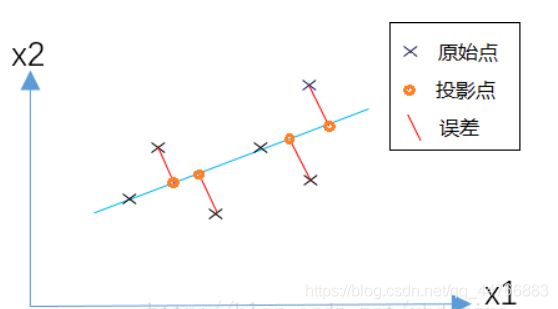
比如我们将下图中的5个点投影到某一维上，这里用一条过原点的直线表示（数据已经中心化）

假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大（也可以说是投影的绝对值之和最大）。

计算投影的方法见下图：

图中，红色点表示样例，蓝色点表示在u上的投影，u是直线的斜率也是直线的方向向量，而且是单位向量。蓝色点是在u上的投影点，离原点的距离是即$X^{T}U$或者$U^{T}X$）。

选择降维后的维度K(主成分的个数)

这里先引入一个概念：PCA误差

PCA的原理是，为了将数据从n维降低到k维，需要找到k个向量，用于投影原始数据，是投影误差（投影距离）最小。

用公式来表示，如下

m表示特征个数

分子表示原始点与投影点之间的距离之和，而误差越小，说明降维后的数据越能完整表示降维前的数据。如果这个误差小于0.01，说明降维后的数据能保留99%的信息。当然这个值可以由我们自己设置，当你觉得误差需要更小，你可以把该值设置的更小。

上式还可以用SVD分解时产生的S矩阵来表示，如下面的式子：

$$1-\frac{{\sum }_1^k{S}_i}{{\sum }_1^m{S}_i}\le 0.01$$

PCA实例

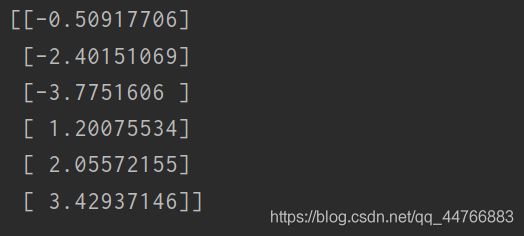
1. PCA的Python实现：

   ##Python实现PCA
   import numpy as np
   
   
   def pca(X, k):  # k is the components you want
       # mean of each feature
       n_samples, n_features = X.shape
       mean = np.array([np.mean(X[:, i]) for i in range(n_features)])
       # normalization
       norm_X = X - mean
       # scatter matrix
       scatter_matrix = np.dot(np.transpose(norm_X), norm_X)
       # Calculate the eigenvectors and eigenvalues
       eig_val, eig_vec = np.linalg.eig(scatter_matrix)
       eig_pairs = [(np.abs(eig_val[i]), eig_vec[:, i]) for i in range(n_features)]
       # sort eig_vec based on eig_val from highest to lowest
       eig_pairs.sort(reverse=True)
       # select the top k eig_vec
       feature = np.array([ele[1] for ele in eig_pairs[:k]])
       # get new data
       data = np.dot(norm_X, np.transpose(feature))
       return data
   
   
   X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
   
   print(pca(X, 1))
   

   上面代码实现了对数据X进行特征的降维。结果如下：