AM、FM、PM调制技术
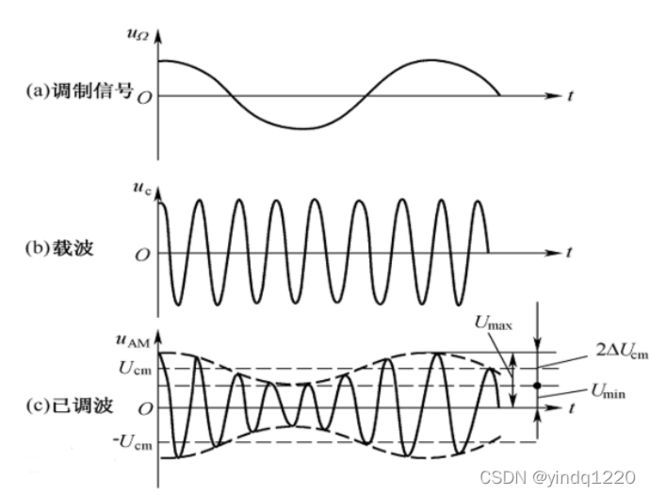
AM调制—幅度调制
-
概念
使载波的振幅按照所需传送信号的变化规律而变化,但频率保持不变的调制方法。
-
优缺点
传播距离远,但是抗干扰能力差。
-
分类
普通调幅:AM
双边带调幅:DSB-AM
单边带调幅:SSB_AM
残留边带条幅:VSB_AM
-
调制信号表达式 调 制 信 号 : U Ω ( t ) = U Ω m cos Ω t {调制信号:U_{\Omega}(t)\ = \ \ U_{\Omega m}\cos}{\Omega t} 调制信号:UΩ(t) = UΩmcosΩt
载 波 信 号 : U c ( t ) = U cm c o s ( w c t ) 载波信号{:U}_{c}(t)\ \ \ = \ \ U_{\text{cm}}cos(w_{c}t) 载波信号:Uc(t) = Ucmcos(wct)
因AM调制的频率不变,采用载波信号的频率,幅度随传送信号变化而变化,因此AM调制后的信号表达式为:
已 调 信 号 : U AM ( t ) = U m ( t ) c o s ( w c t ) 已调信号:U_{\text{AM}}(t)\ = \ U_{m}(t)cos(w_{c}t)\ 已调信号:UAM(t) = Um(t)cos(wct)
= ( U cm + K a U Ω m cos Ω t ) c o s ( w c t ) \ = (U_{\text{cm}}{+ K_{a}U}_{\Omega m}\cos\Omega t)cos(w_{c}t)\ =(Ucm+KaUΩmcosΩt)cos(wct)
= U cm ( 1 + K a U Ω m U cm cos Ω t ) c o s ( w c t ) = U_{\text{cm}}(1 + K_{a}\frac{U_{\Omega m}}{U_{\text{cm}}}\cos\Omega t)cos(w_{c}t)\ =Ucm(1+KaUcmUΩmcosΩt)cos(wct)
其中 m a m_{a} ma为调幅系数: m a m_{a} ma= K a U Ω m U cm K_{a}\frac{U_{\Omega m}}{U_{\text{cm}}} KaUcmUΩm
调幅信号的幅度最大值: U m U_{m} Um(max)=( U cm ( 1 + m a U_{\text{cm}}(1 + m_{a} Ucm(1+ma)
调幅信号的幅度最小值: U m U_{m} Um(min)=( U cm ( 1 − m a U_{\text{cm}}(1 - m_{a} Ucm(1−ma)
因此当 m a m_{a} ma>1时,会出现过调制,即调幅信号的最小值出现负值。
将 U AM ( t ) = U_{\text{AM}}(t)\ = UAM(t) = U cm U_{\text{cm}} Ucm(1 + m a m_{\text{a}} macos Ω \Omega Ω t)cos( w c t ) w_{\text{c}}t) wct)继续展开可得:
U AM ( t ) = U cm c o s ( w c t ) + 1 2 ma U cm c o s ( w c + Ω ) t + 1 2 ma U cm c o s ( w c − Ω ) t U_{\text{AM}}(t) = U_{\text{cm}}cos(w_{c}t) + \frac{1}{2}\text{ma}U_{\text{cm}}cos(w_{c} + \Omega)t + \ \frac{1}{2}\text{ma}U_{\text{cm}}cos(w_{c} - \Omega)t UAM(t)=Ucmcos(wct)+21maUcmcos(wc+Ω)t+ 21maUcmcos(wc−Ω)t
因此得知已调波含有三个频率分量 w c 、 w c + Ω ( 上 边 频 ) w_{c}、w_{c} + \Omega(上边频) wc、wc+Ω(上边频)、 w c − Ω w_{c} - \Omega wc−Ω(下边频)

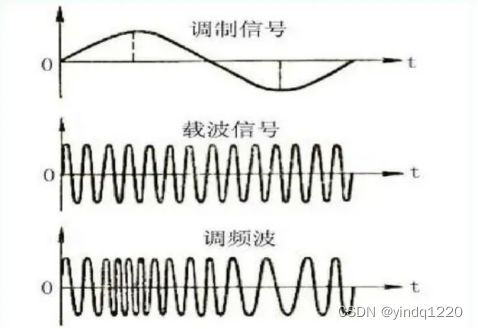
FM调制----频率调制
-
概念
载波的幅度不变,瞬时角频率随调制信号做线性变化。
-
优缺点
抗干扰性强,但是传输距离短。
-
调制信号表达式
调 制 信 号 : U Ω ( t ) = U Ω m cos ( Ω t ) {调制信号:U_{\Omega}(t)\ = \ \ U_{\Omega m}\cos}{(\Omega t)} 调制信号:UΩ(t) = UΩmcos(Ωt)
载 波 信 号 : U c ( t ) = U cm c o s ( w c t ) 载波信号{:U}_{c}(t)\ \ \ = \ \ U_{\text{cm}}cos(w_{c}t) 载波信号:Uc(t) = Ucmcos(wct)
FM调制的瞬时角频率为:
w f ( t ) = w c + k f U Ω ( t ) = w c + k f U Ω m cos Ω t = w c + Δ w fm cos Ω t \ w_{f}(t) = w_{c} + k_{f}U_{\Omega}(t)\ = \ w_{c} + k_{f}{U_{\Omega m}\cos}{\Omega t} = w_{c} + \mathrm{\Delta}w_{\text{fm}}\cos{\Omega t}\ wf(t)=wc+kfUΩ(t) = wc+kfUΩmcosΩt=wc+ΔwfmcosΩt
其中, w c w_{c} wc为载波角频率;
k f k_{f} kf为调频灵敏度,表示单位调制信号幅度引起的频率变化,单位为rad/s.V或者hz/V;
Δ w fm \mathrm{\Delta}w_{\text{fm}} Δwfm为调频波最大角频偏,表示FM波频率摆动的幅度; Δ w fm \mathrm{\Delta}w_{\text{fm}} Δwfm= k f U Ω m k_{f}U_{\Omega m} kfUΩm
调 频 系 数 m f = Δ w fm Ω = k f U Ω m Ω = Δ f m F = Δ φ fm 调频系数\ m_{f} = \frac{\mathrm{\Delta}w_{\text{fm}}}{\Omega} = \frac{k_{f}U_{\Omega m}}{\Omega} = \frac{\mathrm{\Delta}f_{m}}{F} = \mathrm{\Delta}\varphi_{\text{fm}} 调频系数 mf=ΩΔwfm=ΩkfUΩm=FΔfm=Δφfm,时调频时在载波信号的相位加上附加的最大相位偏移,与 U Ω m \ U_{\Omega m} UΩm成正比,与 Ω \Omega Ω成反比。
因此已调信号
U fm ( t ) = U cm cos ( w f ( t ) ∗ t ) = U cm cos ( w c t + m f s i n ( Ω t ) ) {U_{\text{fm}}(t) = U_{\text{cm}}\cos}{(w_{f}(t) \ast t)} = U_{\text{cm}}\cos(w_{c}t + m_{f}\ sin(\Omega t)) Ufm(t)=Ucmcos(wf(t)∗t)=Ucmcos(wct+mf sin(Ωt))
转换后为 U fm ( t ) = U cm cos ( w f ( t ) ∗ t ) = U cm cos ( w c t + k f ∫ 0 t U Ω ( t ) d t ) {U_{\text{fm}}(t) = U_{\text{cm}}\cos}{(w_{f}(t) \ast t)} = U_{\text{cm}}\cos(w_{c}t + k_{f}\ \int_{0}^{t}{U_{\Omega}(t)}dt) Ufm(t)=Ucmcos(wf(t)∗t)=Ucmcos(wct+kf ∫0tUΩ(t)dt)
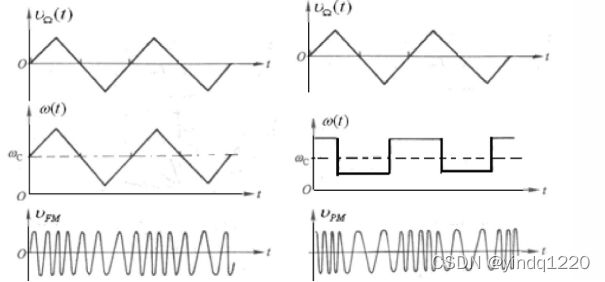
得出结论,调频时,瞬时角频率变化与调制信号成线性关系,瞬时相位的变化与调制信号的积分成线性关系。调频时,频偏反映调制信号的变化规律,相偏正比于调制信号的积分。
从调频波形可知,调频波的波形时等幅的疏密波,波形的疏密反映了调频波瞬时角频率的大小,即调制信号的大小。
PM调制—相位调制
-
概念
载波的相位随调制信号成线性变化。
-
表达式
调 制 信 号 : U Ω ( t ) = U Ω m cos ( Ω t ) {调制信号:U_{\Omega}(t)\ = \ \ U_{\Omega m}\cos}{(\Omega t)} 调制信号:UΩ(t) = UΩmcos(Ωt)
载 波 信 号 : U c ( t ) = U cm c o s ( w c t ) 载波信号{:U}_{c}(t)\ \ \ = \ \ U_{\text{cm}}cos(w_{c}t) 载波信号:Uc(t) = Ucmcos(wct)
调相信号的瞬时相位:
φ ( t ) = w c t + k p U Ω ( t ) = w c t + k p U Ω m cos Ω t \varphi(t)\ = w_{c}t + k_{p}U_{\Omega}(t)\ = \ w_{c}t + k_{p}{U_{\Omega m}\cos}{\Omega t} φ(t) =wct+kpUΩ(t) = wct+kpUΩmcosΩt
瞬时角频率为:
w ( t ) = d φ ( t ) dt = w c + k p d U Ω ( t ) dt = w c + k p U Ω ( t ) w(t) = {\frac{d\varphi(t)}{\text{dt}} = w_{c} + k_{p}\frac{{dU}_{\Omega}(t)\ }{\text{dt}} = w}_{c} + k_{p}U_{\Omega}(t)\ w(t)=dtdφ(t)=wc+kpdtdUΩ(t) =wc+kpUΩ(t)
其中, k p k_{p} kp为调制系数。
由此可以计算调相波的一般表达式:
U p m ( t ) = U cm cos ( φ ( t ) ) = U cm cos ( w c t + k p U Ω ( t ) ) {U_{pm}(t) = U_{\text{cm}}\cos}{(\varphi(t))} = U_{\text{cm}}\cos(w_{c}t + k_{p}U_{\Omega}(t)\ ) Upm(t)=Ucmcos(φ(t))=Ucmcos(wct+kpUΩ(t) )
-
调频和调相的区别
调频和调相都会引起载波在频率和相位上的变化,不过二者变化的规律不同,调频是载波的角频率随调制信号变化,调相是载波的相位随调制信号变化。