【Java】数据结构与算法入门
Java数据结构与算法入门
引言
Java数据结构
- 数据与数据之间的逻辑关系:集合、一对一、一对多、多对多
- 数据的存储结构
线性表:顺序表(比如:集合)、链表、栈、队列
树形结构:二叉树
图形结构
算法
- 排序算法
- 搜索算法
数组中涉及的常见算法
- 数组元素的赋值(杨辉三角、回形数)
- 求数值型数组中元素的最大值、最小值、平均值、总和等
- 数组的复制、反转、查找(线性查找、二分法查找)
- 数组元素的排序算法
十大内部排序算法
-
选择排序
直接选择排序、堆排序 -
交换排序
冒泡排序、快速排序(速度最快) -
插入排序
直接插入排序、折半插入排序、Shell排序 -
归并排序
-
桶式排序
-
基数排序
Arrays工具类
Arrays.sort(arr); // 底层使用快排算法
正文-初级
打印九九乘法表
简单:将九九乘法表打印到控制台。
/*
1.概要设计:
双重循环中
第一次循环代表横坐标,第二次循环代表纵坐标
*/
for (int i = 1; i <10; i++) {
for (int j = 1; j <=i; j++) {
System.out.print(j+" * "+i+" = " + i*j+" ");
}
System.out.println();
}
求1000以内的水仙花数
中等:打印1000以内所有满足水仙花的数,“水仙花数”是指一个三位数其各位数字的立方和等于该数本身,例如153是“水仙花数”,因为:153 = 1^3 + 5^3 + 3^3
/*
1.概要设计:
523 %10=3
523/10 %10=2
523/10/10 %10 =5
* */
for (int i = 100; i <1000; i++) {
int a=i,sum=0;
while (a>0){
int b=a%10;
sum+=b*b*b;
a/=10;
}
if (sum==i) System.out.println(i);
}
青蛙跳台阶问题
困难:一共有n个台阶,一只青蛙每次只能跳一阶或是两阶,那么一共有多少种跳到顶端的方案?例如n=2,那么一共有两种方案,一次性跳两阶或是每次跳一阶。
// 青蛙跳台阶
/*
1.概要设计
n=1,m=1; 一次跳一阶,有一种跳法
n=2,m=1+1=2; 一次跳一阶,剩余一阶,有一种跳法;一次跳2阶,上岸,有一种跳法;
n=3,m=2+1=3; 一次跳一阶,剩余2阶,有两种跳法;一次跳2阶,剩余一阶,有一种跳法;
n=4,m=3+2=5; 一次跳一阶,剩余3阶,有3种跳法;一次跳2阶,剩余2阶,有两种跳法;
...
可以看到,每次多一阶,跳法都是前两次跳法的和
2.设计答疑:
那么我们为什么不算上一次跳n阶台阶呢,比如,n=3,为什么不这样写?
n=3,m=2+1+1=4; 一次跳一阶,剩余2阶,有两种跳法;一次跳2阶,剩余一阶,有一种跳法;一次跳3阶,只有一种跳法
原因很简单,因为我们这里用的方法是用已知求未知:即,已经知道n=1,和n=2的时候,m的值,我们不妨充分利用这个数值。
3.时间复杂度问题
当n足够大的时候,这些数据的计算量还是有一丢丢耗时的,
如果不把每次计算出来的结果存储一下,计算下一个m的时候,还需要重复上一次m的计算。很耗时。
所以要把数据存储下来以节约时间,降低时间开销。
ps:这里的时间复杂度是n,但是使用递归来计算,时间复杂度是n的n次方。
*/
int[] ints = new int[45];
ints[0]=1;
ints[1]=2;
for (int i = 2; i <ints.length; i++) {
ints[i]=ints[i-1]+ints[i-2];
System.out.println(ints[i]);
}
三大基本排序算法
- 冒泡排序
冒泡排序就是冒泡,其实就是不断使得我们无序数组中的最大数向前移动,经历n轮循环逐渐将每一个数推向最前。
public static void main(String[] args) {
// 冒泡排序
int query[] = {1, 5, 6, 2, 0, 14, 52, 32, 98};
test(query);
for (int j = 0; j <query.length; j++) {
System.out.print(query[j]+" ");
}
}
public static void test(int query[]){
for (int i = 0; i < query.length - 1; i++) {
boolean lock=true;//优化锁
for (int j = 0; j <query.length-1; j++) {
if (query[j]<query[j+1]){
lock=false;
int temp=query[j];
query[j]=query[j+1];
query[j+1]=temp;
}
}
if (lock) break;
}
}
- 插入排序
插入排序其实就跟我们打牌是一样的,我们在摸牌的时候,牌堆是乱序的,但是我们一张一张摸到手中进行排序,使得它变成了有序的!

public static void main(String[] args) {
// 插入排序
int query[] = {1, 5, 6, 2, 0, 14, 52, 32, 98};
test(query);
for (int i = 0; i < query.length; i++) {
System.out.print(query[i] + " ");
}
}
public static void test(int query[]) {
for (int i = 1; i < query.length; i++) {
int temp = query[i];
int j = i - 1;
while (j >= 0 && temp < query[j]) {
query[j + 1] = query[j];
j--;
}
query[j + 1] = temp;
}
}
- 选择排序
选择排序其实就是每次都选择当前数组中最大的数排到最前面!
public static void main(String[] args) {
// 选择排序
int query[] = {1, 5, 6, 2, 0, 14, 52, 32, 98};
test(query);
for (int i = 0; i < query.length; i++) {
System.out.print(query[i] + " ");
}
}
public static void test(int[] query) {
for (int i = 0; i < query.length-1; i++) {
int max = query[i],p = i;
for (int j = i+1; j < query.length; j++) {
if (query[j] > max){
max = query[j];
p=j;
}
}
int temp=query[p];
query[p]=query[i];
query[i]=temp;
}
}
面向对象编程实战
- 二分搜索(搜索算法)
现在有一个有序数组(从小到大,数组长度 0 < n < 1000000)如何快速寻找我们想要的数在哪个位置,如果存在请返回下标,不存在返回-1即可。
public static void main(String[] args) {
// 二分查找
int[] arr = new int[]{1, 2, 5, 9, 10, 23, 50, 88, 99, 101};
System.out.println(test(arr, 88));
}
public static int test(int[] arr, int find) {
int start = 0, end = arr.length - 1;
while (start <= end) {
int mid = (start + end + 1) / 2;
if (find == arr[mid]) return mid;
if (find < arr[mid]) end = mid - 1;
if (find > arr[mid]) start = mid + 1;
}
return -1;
}
- 快速排序(排序算法、递归分治)
(开始之前先介绍一下递归!)快速排序其实是一种排序执行效率很高的排序算法,它利用分治法来对待排序序列进行分治排序,它的思想主要是通过一趟排序将待排记录分隔成独立的两部分,其中的一部分比关键字小,后面一部分比关键字大,然后再对这前后的两部分分别采用这种方式进行排序,通过递归的运算最终达到整个序列有序。
快速排序就像它的名字一样,快速!
public static void main(String[] args) {
// 插入排序
int query[] = {1, 5, 6, 2, 0, 14, 52, 32, 98};
test(query, 0, query.length - 1);
for (int i = 0; i < query.length; i++) {
System.out.print(query[i] + " ");
}
}
public static void test(int[] query, int start, int end) {
if (start >= end) return;
int key = query[start], left = start, right = end;
while (left < right) {
while (query[right] >= key && left < right) right--;
query[left] = query[right];
while (query[left] <= key && left < right) left++;
query[right] = query[left];
}
query[left] = key;
test(query, start, right - 1);
test(query, right + 1, end);
}
- 0/1背包问题(回溯法、剪枝/动态规划优化)
小偷来到商店偷东西,商店有 n件物品,每一个物品的重量为 w[n],每个物品的价值为 v[n]。现挑选物品放入背包中,假定背包能承受的最大重量为 capacity,背包中最多只能存放number件物品,小偷如何装背包可以使带走东西的价值最大?
static int [] value={3,4,5,8,10};
static int [] weight={2,3,4,5,9};
static int band=20, i= weight.length-1;//这里存放一些数组索引和背包容量
public static void main(String[] args) {
System.out.println(test(0, 0));
}
public static int test(int index,int backage){
// 如果索引越界,则返回
if (index> i) return 0;
// 如果选择后后重量超出,则返回
if (backage+weight[index]>band) return 0;
// 左边是选择,右边是不选择
return Math.max(value[index]+test(index+1,backage+weight[index]),test(index+1,backage));
}
中级-数据结构基础
引言
在计算机科学中,数据结构是一种数据组织、管理和存储的格式,它可以帮助我们实现对数据高效的访问和修改。更准确地说,数据结构是数据值的集合,可以体现数据值之间的关系,以及可以对数据进行应用的函数或操作。
通俗地说,我们需要去学习在计算机中如何去更好地管理我们的数据,才能让我们对我们的数据控制更加灵活!
线性表
线性表是最基本的一种数据结构,它是表示一组相同类型数据的有限序列,你可以把它与数组进行参考,但是它并不是数组,线性表是一种表结构,它能够支持数据的插入、删除、更新、查询等,同时数组可以随意存放在数组中任意位置,而线性表只能依次有序排列,不能出现空隙,因此,我们需要进一步的设计。
- 顺序表
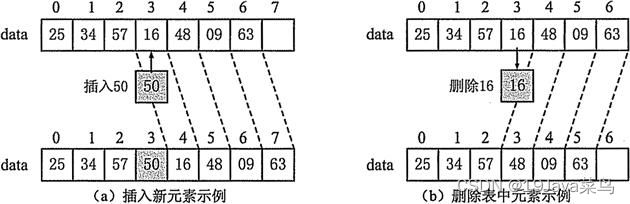
将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构,而以这种方式实现的线性表,我们称为顺序表。
同样的,表中的每一个个体都被称为元素,元素左边的元素(上一个元素),称为前驱,同理,右边的元素(后一个元素)称为后驱。
我们设计线性表的目标就是为了去更好地管理我们的数据,也就是说,我们可以基于数组,来进行封装,实现增删改查!既然要存储一组数据,那么很容易联想到我们之前学过的数组,数组就能够容纳一组同类型的数据。
目标:以数组为底层,编写以下抽象类的具体实现
/** * 线性表抽象类 * @param 存储的元素(Element)类型 */
public abstract class AbstractLink<E> {
/** * 获取表的长度 */
public abstract int size();
/** * 添加一个元素 */
public abstract void add(E e, int index);
/** * 移除指定位置的元素 */
public abstract E remove(int index);
/** * 获取指定位置的元素 */
public abstract E get(int index);
}
实现类
//顺序表
public class ArrayList<E> extends AbstractLink<E>{
private Object [] and=new Object[1];
private int size=0;
@Override
public void add(int index, E e) {
//判断索引是否非法
if (index>size) throw new IndexOutOfBoundsException("非法插入位置");
//扩容
if (size>=and.length){
Object and[]= new Object[this.and.length+10];
for (int i = 0; i <this.and.length; i++) {
and[i]=this.and[i];
}
this.and=and;
}
//元素后移
int i=size;
while (i>index) {
and[i]=and[i-1];
i--;
}
and[index]=e;
size++;
}
@Override
public E remove(int index) {
if (index>size) throw new IndexOutOfBoundsException("非法删除位置");
int i=index;
E e= (E) and[index];
while (i<size){
and[i]=and[i+1];
i++;
}
size--;
return e;
}
@Override
public int size() {
return size;
}
@Override
public E get(int index) {
if (index>=size) throw new IndexOutOfBoundsException("索引越界");
return (E) and[index];
}
}
- 链表
数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构
实际上,就是每一个结点存放一个元素和一个指向下一个结点的引用(C语言里面是指针,Java中就是对象的引用,代表下一个结点对象)
public class LinkedList<E> extends AbstractLink<E> {
private Node<E> head = new Node<>(null);
private int size = 0;
@Override
public int size() {
return size;
}
@Override
public void add(int index, E e) {
// 判断索引是否非法
if (index > size) throw new IndexOutOfBoundsException("插入失败");
// 设置头节点
Node<E> node = head, temp;
// 寻找查找位置
for (int i = 0; i < index; i++) node = node.next;
// 记录索引处结点
temp = node.next;
// 插入元素
node.next = new Node<>(e);
node.next.next = temp;
size++;
}
@Override
public E remove(int index) {
if (index > size) throw new IndexOutOfBoundsException("删除失败");
// 设置头节点
Node<E> node = head, temp;
// 寻找查找位置
for (int i = 0; i < index; i++) node = node.next;
// 记录索引处结点
temp = node.next;
// 删除元素
node.next = node.next.next;
return temp.e;
}
@Override
public E get(int index) {
if (index >= size) throw new IndexOutOfBoundsException("数据不存在");
// 设置头节点
Node<E> node = head, temp;
// 寻找查找位置
for (int i = 0; i < index; i++) node = node.next;
// 记录索引处结点
temp=node.next;
return temp.e;
}
private static class Node<E> {
private E e;
private Node<E> next;
public Node(E e) {
this.e = e;
}
}
}
利用这种思想,我们再来尝试实现上面的抽象类,从实际的代码中感受!
比较:顺序表和链表的优异?
顺序表优缺点:
- 访问速度快,随机访问性能高
- 插入和删除的效率低下,极端情况下需要变更整个表
- 不易扩充,需要复制并重新创建数组
链表优缺点:
- 插入和删除效率高,只需要改变连接点的指向即可
- 动态扩充容量,无需担心容量问题
- 访问元素需要依次寻找,随机访问元素效率低下
- 链表只能指向后面,能不能指向前面呢?双向链表!
栈和队列实际上就是对线性表加以约束的一种数据结构,如果前面的线性表的掌握已经ok,那么栈和队列就非常轻松了!
- 栈
栈遵循先入后出原则,只能在线性表的一端添加和删除元素。我们可以把栈看做一个杯子,杯子只有一个口进出,最低处的元素只能等到上面的元素离开杯子后,才能离开。
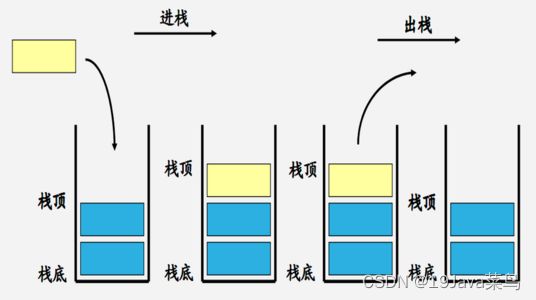
向栈中插入一个元素时,称为入栈(压栈),移除栈顶元素称为出栈,我们需要尝试实现以下抽象类型:
/** * 抽象类型栈,待实现 * @param 元素类型 */
public abstract class AbstractStack<E> {
/** * 出栈操作 * @return 栈顶元素 */
public abstract E pop();
/** * 入栈操作 * @param e 元素 */
public abstract void push(E e);
}
实现类
public class ArrayStack<E> extends AbstractStack<E> {
private Object[] and=new Object[1];
private int size=0;
@Override
public E pop() {
return (E) and[--size];
}
@Override
public void push(E e) {
// 扩容
if (size>=and.length){
Object[] objects = new Object[and.length + 1];
for (int i = 0; i <and.length; i++) objects[i]=and[i];
and=objects;
}
and[size++]=e;
}
}
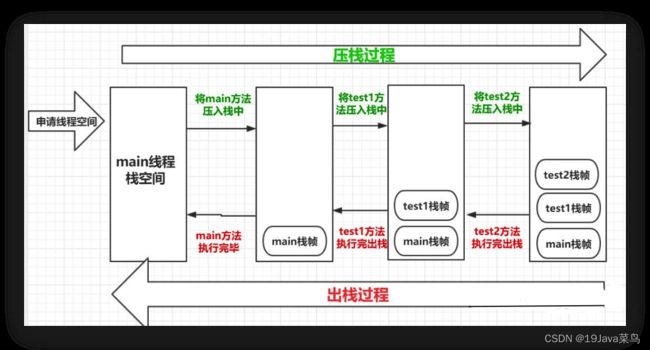
其实,我们的JVM在处理方法调用时,也是一个栈操作:
如:
public static void main(String[] args) {
test1();
}
public static void test1(){
test2();
}
public static void test2(){
}
此时JVM的流程如下:
所以说,如果玩不好递归,就会像这样:
public class Main {
public static void main(String[] args) {
go();
}
private static void go(){
go();
}
}
Exception in thread "main" java.lang.StackOverflowError
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
at com.test.Main.go(Main.java:13)
...
栈的深度是有限制的,如果达到限制,将会出现StackOverflowError错误(注意是错误!说明是JVM出现了问题)
- 队列
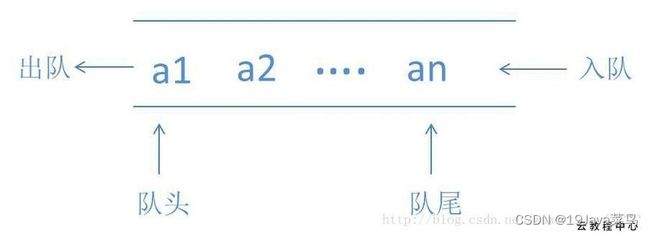
队列同样也是受限制的线性表,列就像排队一样,只能从队尾排,从队首出,即先进先出。
所以我们要实现以下内容:
/** * * @param */
public abstract class AbstractQueue<E> {
/** * 进队操作 */
public abstract void offer(E e);
/** * 出队操作 */
public abstract E poll();
}
实现类
public class ArrayQueue<E> extends AbstractQueue<E> {
private Object[] and = new Object[3];
private int head = 0, tail = 0;
@Override
public void offer(E e) {
int next=(tail+1)%and.length;
if (next==head) return;
and[tail] = e;
tail=next;
}
@Override
public E poll() {
E e = (E) and[head];
head = (head + 1) % and.length;
return e;
}
}
二叉树
本版块主要是二叉树,树也是一种数据结构,但是它使用起来更加的复杂。
- 树
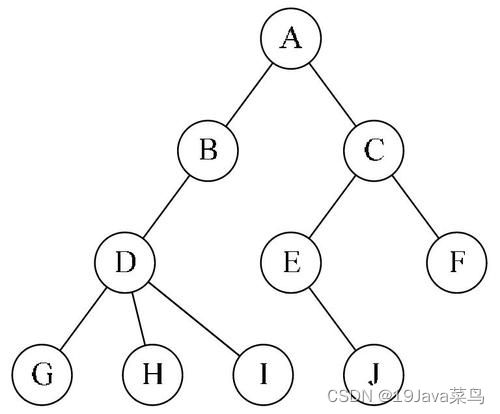
链表是单个结点之间相连,也就是一种一对一的关系,而树则是一个结点连接多个结点,也就是一对多的关系。
一个结点可以有N个子结点,就像上图一样,看起来就像是一棵树。而位于最顶端的结点(没有父结点)我们称为根结点,而结点拥有的子节点数量称为度,每向下一级称为一个层次,树中出现的最大层次称为树的深度(高度)。
- 二叉树
二叉树是一种特殊的树,每个结点最多有两颗子树,所以二叉树中不存在度大于2的结点,位于两边的子结点称为左右子树
注:左右子树是明确区分的,是左就是左,是右就是右
数学性质:
- 在二叉树的第i层上最多有2(i-1) 个节点。
- 二叉树中如果深度为k,那么最多有2k-1个节点。
设计一个二叉树结点类:
public class TreeNode<E> {
public E e;//当前节点数据
public TreeNode<E> left;//左子树
public TreeNode<E> right;//右子树
public TreeNode(E e){
this.e=e;
}
}
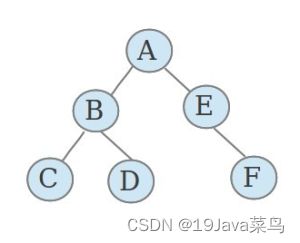
上图二叉树实现
public static void main(String[] args) {
TreeNode<String> root = new TreeNode<String>("A");
root.left=new TreeNode<>("B");
root.right=new TreeNode<>("E");
root.left.left=new TreeNode<>("C");
root.left.right=new TreeNode<>("D");
root.right.right=new TreeNode<>("F");
System.out.println("debug");
}
- 二叉树的遍历
顺序表的遍历其实就是依次有序去访问表中每一个元素,而像二叉树这样的复杂结构,我们有四种遍历方式,他们是:前序遍历、中序遍历、后序遍历以及层序遍历,本版块主要讨论前三种遍历方式:
- 前序遍历:从二叉树的根结点出发,到达结点时就直接输出结点数据,按照先向左在向右的方向访问。ABCDEF,即:
根左右 - 中序遍历:从二叉树的根结点出发,优先输出左子树的节点的数据,再输出当前节点本身,最后才是右子树。CBDAEF,即,
左根右 - 后序遍历:从二叉树的根结点出发,优先遍历其左子树,再遍历右子树,最后在输出当前节点本身。CDBFEA,即,
左右根
注:这里的前序中序后序指的是根的排序位次:前中后。
算法实现
public static void main(String[] args) {
TreeNode<String> root = new TreeNode<String>("A");
root.left=new TreeNode<>("B");
root.right=new TreeNode<>("E");
root.left.left=new TreeNode<>("C");
root.left.right=new TreeNode<>("D");
root.right.right=new TreeNode<>("F");
System.out.println("debug");
before(root);
System.out.println("前序遍历");
center(root);
System.out.println("中序遍历");
after(root);
System.out.println("后序遍历");
}
// 前序遍历
public static void before(TreeNode<String> e){
if (e==null) return;
System.out.print(e.e+ " ");
before(e.left);
before(e.right);
}
// 中序遍历
public static void center(TreeNode<String> e){
if (e==null) return;
center(e.left);
System.out.print(e.e+ " ");
center(e.right);
}
// 后序遍历
public static void after(TreeNode<String> e){
if (e==null) return;
after(e.left);
after(e.right);
System.out.print(e.e+ " ");
}
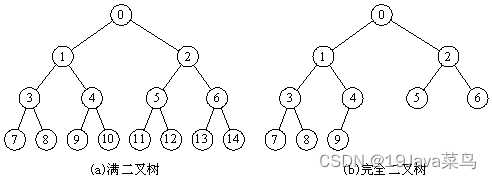
- 满二叉树和完全二叉树
满二叉树和完全二叉树其实就是特殊情况下的二叉树:
满二叉树的每一个层级都给加满了结点。完全二叉树与满二叉树不同的地方在于,它的最下层叶子节点可以不满,但最下层的叶子节点必须从左到右排布(靠左排布)。
其实满二叉树和完全二叉树就是有一定规律的二叉树,很容易理解。
快速查找
数据结构,可以很好地帮我们管理了数据。那么如果需要查找某一个元素是否存在于数据结构中,如何才能更加高效的去完成呢?
- 哈希表
我们发现,顺序表虽然查询效率高,但是插入删除有严重表更新的问题。而链表虽弥补了更新问题,但查询效率实在是太低了!由此,哈希表给了一套折中的方案,其融合顺序表和链表于一体。
画外音:我们发现,Object类中,定义了一个叫做hashcode()的方法,而这个方法就是为了更好地支持哈希表的实现。hashcode()默认得到的是对象的内存地址,也就是说,每个对象的hashCode都不一样。
哈希表,其实本质上就是一个存放链表的数组,下面是它的模样:
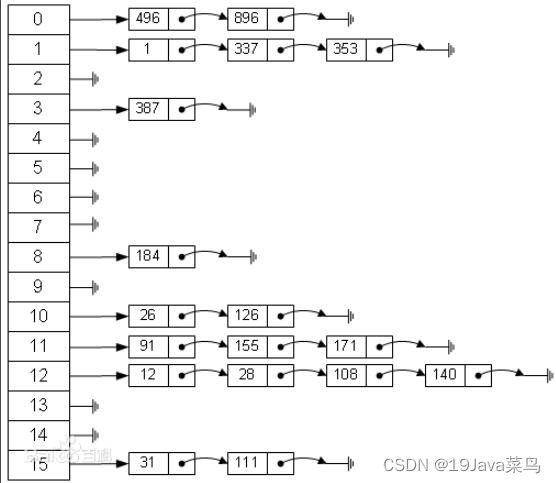
数组中每一个元素都是一个头结点,用于保存数据,通过hash算法,我们能够瞬间得到元素应该放置的位置。
//假设hash表长度为16,hash算法为:
private int hash(int hashcode){
return hashcode % 16;
}
问题:如果计算出来的hash值和之前已经存在的元素相同了,这种情况我们称为hash碰撞,这也是为什么要将每一个表元素设置为一个链表的头结点的原因,一旦发现重复,我们可以往后继续添加节点。
当然,以上的hash表结构只是一种设计方案,在面对大额数据时,是不够用的,在JDK1.8中,集合类使用的是数组+二叉树的形式解决的(这里的二叉树是经过加强的二叉树,不是前面讲得简单二叉树,我们下一节就会开始讲)
- 二叉排序树
我们前面学习的二叉树效率是不够的,我们需要的是一种效率更高的二叉树,因此,基于二叉树的改进,提出了二叉查找树,可以看到结构像下面这样:
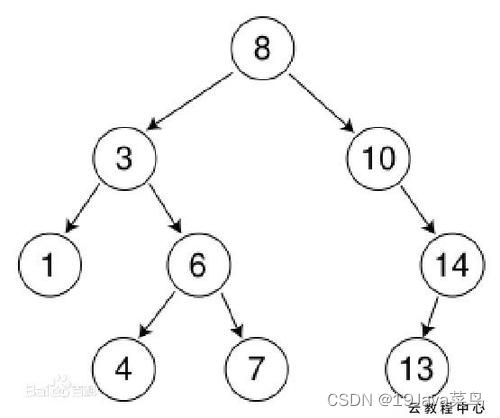
不难发现,每个节点的左子树,一定小于当前节点的值,每个节点的右子树,一定大于当前节点的值,这样的二叉树称为二叉排序树。利用二分搜索的思想,我们就可以快速查找某个节点!
同时,对二叉树中序遍历即可对节点数字排序。
- 平衡二叉树
在了解了二叉查找树之后,我们发现,如果根节点为10,现在加入到结点的值从9开始,依次减小到1,那么这个表就会很奇怪,就像下面这样:
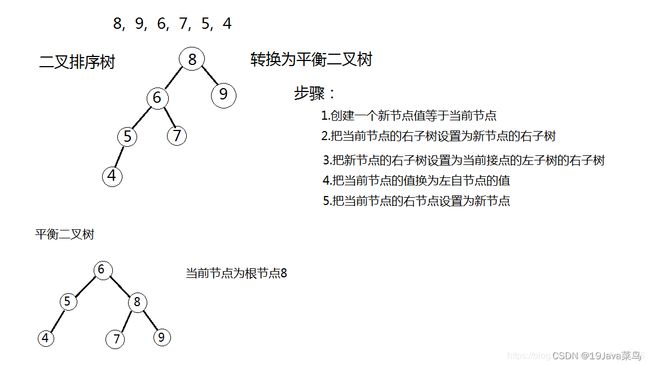
显然,当所有的结点都排列到一边,这种情况下,查找效率会直接退化为最原始的二叉树!因此我们需要维持二叉树的平衡,才能维持原有的查找效率。
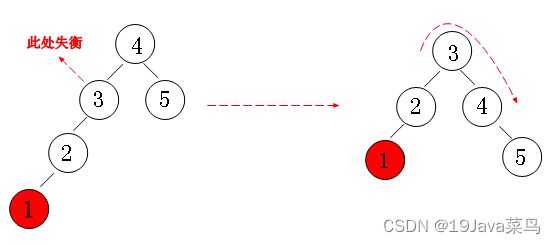
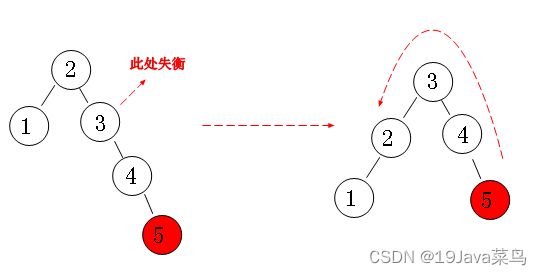
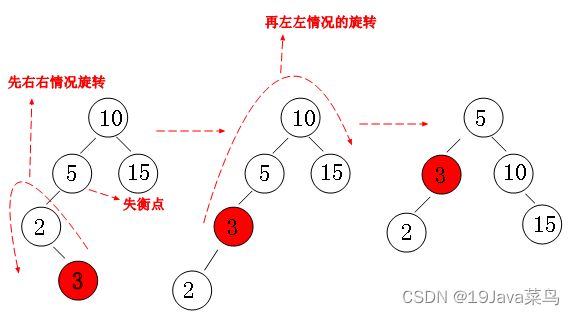
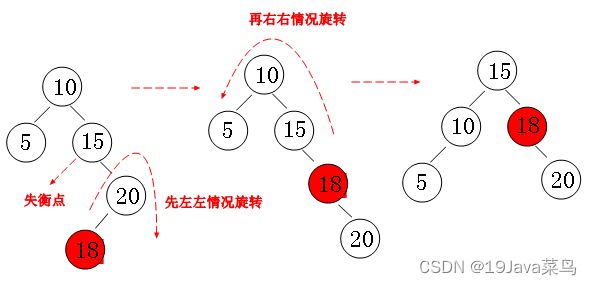
现在我们对二叉排序树加以约束,要求每个结点的左右两个子树的高度差的绝对值不超过1,这样的二叉树称为平衡二叉树,同时要求每个结点的左右子树都是平衡二叉树,这样,就不会因为一边的疯狂增加导致失衡。我们来看看以下几种情况:
左左失衡
右右失衡
左右失衡
右左失衡
通过以上四种情况的处理,最终得到维护平衡二叉树的算法。
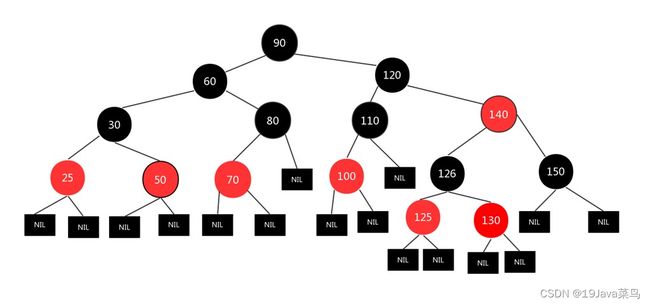
- 红黑树
红黑树也是二叉排序树的一种改进,同平衡二叉树一样,红黑树也是一种维护平衡的二叉排序树,但是没有平衡二叉树那样严格(平衡二叉树每次插入新结点时,可能会出现大量的旋转,而红黑树保证不超过三次),红黑树降低了对于旋转的要求,因此效率有一定的提升同时实现起来也更加简单。但是红黑树的效率却高于平衡二叉树,红黑树也是JDK1.8中使用的数据结构!
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点的两边也需要表示(虽然没有,但是null也需要表示出来)是黑色。
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
节点插入红黑树的插入规则:
1. 将新插入的节点标记为红色
2. 如果 X 是根结点(root),则标记为黑色
3. 如果 X 的 parent 不是黑色,同时 X 也不是 root:
if(X 的 uncle (叔叔) 是红色){
1> 将 parent 和 uncle 标记为黑色
2> 将 grand parent (祖父) 标记为红色
3> 让 X 节点的颜色与 X 祖父的颜色相同,然后重复步骤 2、3
}
if( X 的 uncle (叔叔) 是黑色){
左左 if(P 是 G 的左孩子,并且 X 是 P 的左孩子)
左右 if(P 是 G 的左孩子,并且 X 是 P 的右孩子)
右右 if(P 是 G 的右孩子,并且 X 是 P 的右孩子)
右左 if(P 是 G 的右孩子,并且 X 是 P 的左孩子)
}
认识集合类
集合表示一组对象,称为其元素。一些集合允许重复的元素,而另一些则不允许。一些集合是有序的,而其他则是无序的。
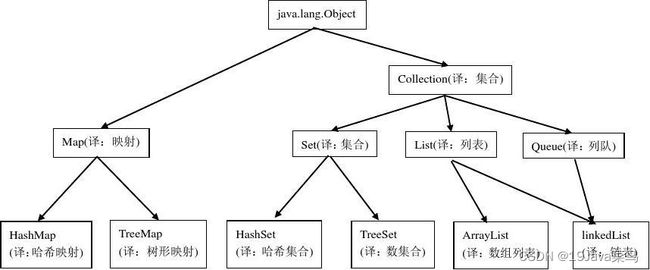
集合类其实就是为了更好地组织、管理和操作我们的数据而存在的,包括列表、集合、队列、映射等数据结构。这一块从源码角度进行分析(数据结构很重要!),不仅仅是只会如何去使用。
集合类最顶层是接口,因为接口代表的是某个功能,而抽象类是已经快要成形的类型,不同的集合类的底层实现是不相同的,同时一个集合类可能会同时具有两种及以上功能(既能做队列也能做列表),所以采用接口会更加合适,接口只需定义支持的功能即可。
数组与集合
相同之处:
- 它们都是容器,都能够容纳一组元素。
不同之处:
- 数组的大小是固定的,集合的大小是可变的。
- 数组可以存放基本数据类型,但集合只能存放对象。
- 数组存放的类型只能是一种,但集合可以有不同种类的元素。
- 集合根接口Collection
此接口中定义了全部的集合基本操作,可以在源码中看看。
再看List和Set以及Queue接口的源码。
集合类的使用
- List列表
首先介绍ArrayList,它的底层是用数组实现的,内部维护的是一个可改变大小的数组,也就是之前所说的线性表!跟之前自己写的ArrayList相比,它更加的规范,同时继承自List接口。
先看看ArrayList的源码!
基本操作
List<String> list = new ArrayList<>(); //默认长度的列表
List<String> listInit = new ArrayList<>(100); //初始长度为100的列表
向列表中添加元素:
public static void main(String[] args) {
List<String> and=new ArrayList<>();
and.add("a");
and.add("b");
System.out.println(and);
System.out.println(and.contains("a"));
System.out.println(and.contains("c"));
List<Student> band=new ArrayList<>();
band.add(new Student("a"));
band.add(new Student("b"));
// 此处比较的是equals()方法
System.out.println(band.contains(new Student("a")));
}
注:这里的contains()方法比较的是equals()方法。
移除元素:
public static void main(String[] args) {
List<String> list = new ArrayList<>();
list.add("lbwnb");
list.add("yyds");
list.remove(0); //按下标移除元素
list.remove("yyds"); //移除指定元素
System.out.println(list);
}
也支持批量操作:
public static void main(String[] args) {
ArrayList<String> list = new ArrayList<>();
list.addAll(new ArrayList<>()); //在尾部批量添加元素
list.removeAll(new ArrayList<>()); //批量移除元素(只有给定集合中存在的元素才会被移除)
list.retainAll(new ArrayList<>()); //只保留某些元素
System.out.println(list);
}
我们再来看LinkedList,其实本质就是一个链表!
来看看源码
其实与之前编写的LinkedList不同之处在于,它内部使用的是一个双向链表:
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
当然,它还实现了Queue接口,所以LinkedList也能被当做一个队列或是栈来使用。
public static void main(String[] args) {
LinkedList<String> list = new LinkedList<>();
list.offer("A"); //入队
System.out.println(list.poll()); //出队
list.push("A");
list.push("B"); //进栈
list.push("C");
System.out.println(list.pop());
System.out.println(list.pop()); //出栈
System.out.println(list.pop());
}
利用代码块来快速添加内容
之前的匿名内部类,就可以利用代码块,来快速生成一个自带元素的List
List<String> list = new LinkedList<String>(){{ //初始化时添加
this.add("A"); this.add("B");
}
};
如果是需要快速生成一个只读的List,可以看下文的Arrays工具类。
集合的排序
List<Integer> list = new LinkedList<Integer>(){ //Java9才支持匿名内部类使用钻石运算符 {
this.add(10);
this.add(2);
this.add(5);
this.add(8);
}};
list.sort((a, b) -> { //排序已经由JDK实现,现在只需要填入自定义规则,完成Comparator接口实现
return a - b; //返回值小于0,表示a应该在b前面,返回值大于0,表示b应该在a后面,等于0则不进行交换
});
System.out.println(list);
迭代器
集合的遍历
所有的集合类,都支持foreach循环!
public static void main(String[] args) {
List<Integer> list = new LinkedList<Integer>(){ //Java9才支持匿名内部类使用钻石运算符 {
this.add(10);
this.add(2);
this.add(5);
this.add(8);
} };
for (Integer integer : list) {
System.out.println(integer);
}
}
当然,也可以使用JDK1.8新增的forEach方法,它接受一个Consumer接口实现:
list.forEach(i -> { System.out.println(i);});
从JDK1.8开始,lambda表达式开始逐渐成为主流,我们需要去适应函数式编程的这种语法,包括批量替换,也是用到了函数式接口来完成的。
list.replaceAll((i) -> {
if(i == 2) return 3; //将所有的2替换为3
else return i; //不是2就不变
});
System.out.println(list);
Iterable和Iterator接口
之前学习数据结构时,已经得知,不同的线性表实现,在获取元素时的效率也不同,因此需要一种更好地方式来统一不同数据结构的遍历。
由于ArrayList对于随机访问的速度更快,而LinkedList对于顺序访问的速度更快,因此在上述的传统for循环遍历操作中,ArrayList的效率更胜一筹,因此我们要使得LinkedList遍历效率提升,就需要采用顺序访问的方式进行遍历,如果没有迭代器帮助我们统一标准,那么我们在应对多种集合类型的时候,就需要对应编写不同的遍历算法,很显然这样会降低我们的开发效率,而迭代器的出现就帮助我们解决了这个问题。
我们先来看看迭代器里面方法:
public interface Iterator<E> { //...}
每个集合类都有自己的迭代器,通过iterator()方法来获取:
Iterator<Integer> iterator = list.iterator(); //生成一个新的迭代器while
(iterator.hasNext()){ //判断是否还有下一个元素
Integer i = iterator.next(); //获取下一个元素(获取一个少一个)
System.out.println(i);
}
迭代器生成后,默认指向第一个元素,每次调用next()方法,都会将指针后移,当指针移动到最后一个元素之后,调用hasNext()将会返回false,迭代器是一次性的,用完即止,如果需要再次使用,需要调用iterator()方法。
ListIterator<Integer> iterator = list.listIterator();
//List还有一个更好地迭代器实现ListIterator
ListIterator是List中独有的迭代器,在原有迭代器基础上新增了一些额外的操作。
Set集合
我们之前已经看过Set接口的定义了,我们发现接口中定义的方法都是Collection中直接继承的,因此,Set支持的功能其实也就和Collection中定义的差不多,只不过使用方法上稍有不同。
Set集合特点:
- 不允许出现重复元素
- 不支持随机访问(不允许通过下标访问)
首先认识一下HashSet,它的底层就是采用哈希表实现的(我们在这里先不去探讨实现原理,因为底层实质上维护的是一个HashMap,我们学习了Map之后再来讨论)
public static void main(String[] args) {
HashSet<Integer> set = new HashSet<>();
set.add(120); //支持插入元素,但是不支持指定位置插入
set.add(13);
set.add(11);
for (Integer integer : set) {
System.out.println(integer);
}
}
运行上面代码发现,最后Set集合中存在的元素顺序,并不是我们的插入顺序,这是因为HashSet底层是采用哈希表来实现的,实际的存放顺序是由Hash算法决定的。
那么我们希望数据按照我们插入的顺序进行保存该怎么办呢?我们可以使用LinkedHashSet:
public static void main(String[] args) {
LinkedHashSet<Integer> set = new LinkedHashSet<>(); //会自动保存我们的插入顺序
set.add(120);
set.add(13);
set.add(11);
for (Integer integer : set) {
System.out.println(integer);
}
}
LinkedHashSet底层维护的不再是一个HashMap,而是LinkedHashMap,它能够在插入数据时利用链表自动维护顺序,因此这样就能够保证我们插入顺序和最后的迭代顺序一致了。
还有一种Set叫做TreeSet,它会在元素插入时进行排序:
public static void main(String[] args) {
TreeSet<Integer> set = new TreeSet<>();
set.add(1);
set.add(3);
set.add(2);
System.out.println(set);
}
可以看到最后得到的结果并不是我们插入顺序,而是按照数字的大小进行排列。当然,我们也可以自定义排序规则:
public static void main(String[] args) {
TreeSet<Integer> set = new TreeSet<>((a, b) -> b - a); //在创建对象时指定规则即可
set.add(1);
set.add(3);
set.add(2);
System.out.println(set);
}
现在的结果就是我们自定义的排序规则了。
虽然Set集合只是粗略的进行了讲解,但是学习Map之后,我们还会回来看我们Set的底层实现,所以说最重要的还是Map。本节只需要记住Set的性质、使用即可。
Map映射
什么是映射
我们在高中阶段其实已经学习过映射了,映射指两个元素的之间相互“对应”的关系,也就是说,我们的元素之间是两两对应的,是以键值对的形式存在。
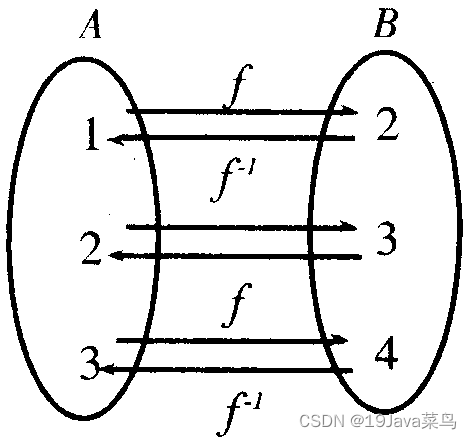
Map接口
Map就是为了实现这种数据结构而存在的,我们通过保存键值对的形式来存储映射关系。
我们先来看看Map接口中定义了哪些操作。
HashMap和LinkedHashMap
HashMap的实现过程,相比List,就非常地复杂了,它并不是简简单单的表结构,而是利用哈希表存放映射关系,我们来看看HashMap是如何实现的,首先回顾我们之前学习的哈希表,它长这样:
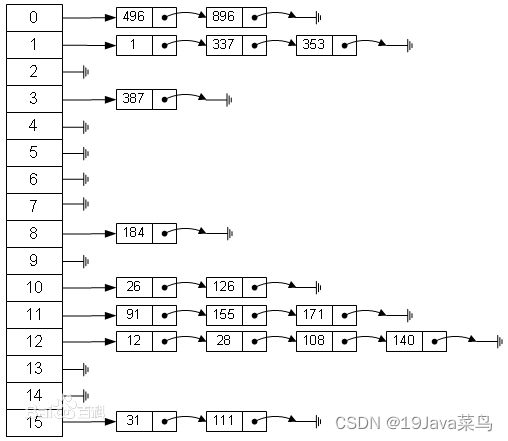
哈希表的本质其实就是一个用于存放后续节点的头结点的数组,数组里面的每一个元素都是一个头结点(也可以说就是一个链表),当要新插入一个数据时,会先计算该数据的哈希值,找到数组下标,然后创建一个新的节点,添加到对应的链表后面。
而HashMap就是采用的这种方式,我们可以看到源码中同样定义了这样的一个结构:
/** * The table, initialized on first use, and resized as
* necessary. When allocated, length is always a power of two.
* (We also tolerate length zero in some operations to allow
* bootstrapping mechanics that are currently not needed.) */
transient Node<K,V>[] table;
这个表会在第一次使用时初始化,同时在必要时进行扩容,并且它的大小永远是2的倍数!
/** * The default initial capacity - MUST be a power of two. */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
我们可以看到默认的大小为2的4次方,每次都需要是2的倍数,也就是说,下一次增长之后,大小会变成2的5次方。
我们现在需要思考一个问题,当我们表中的数据不断增加之后,链表会变得越来越长,这样会严重导致查询速度变慢,首先想到办法就是,我们可以对数组的长度进行扩容,来存放更多的链表,那么什么情况下会进行扩容呢?
/** * The load factor for the hash table.
* * @serial */
final float loadFactor;
我们还发现HashMap源码中有这样一个变量,也就是负载因子,那么它是干嘛的呢?
负载因子其实就是用来衡量当前情况是否需要进行扩容的标准。我们可以看到默认的负载因子是0.75
/** * The load factor used when none specified in constructor. */
static final float DEFAULT_LOAD_FACTOR = 0.75f;
那么负载因子是怎么控制扩容的呢?0.75的意思是,在插入新的结点后,如果当前数组的占用率达到75%则进行扩容。在扩容时,会将所有的数据,重新计算哈希值,得到一个新的下标,组成新的哈希表。
但是这样依然有一个问题,链表过长的情况还是有可能发生,所以,为了从根源上解决这个问题,在JDK1.8时,引入了红黑树这个数据结构。
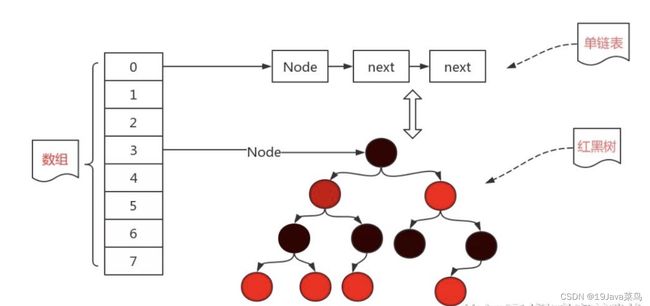
当链表的长度达到8时,会自动将链表转换为红黑树,这样能使得原有的查询效率大幅度降低!当使用红黑树之后,我们就可以利用二分搜索的思想,快速地去寻找我们想要的结果,而不是像链表一样挨个去看。
/** * Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn
* extends Node) so can be used as extension of either regular or
* linked node. */
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
除了Node以外,HashMap还有TreeNode,很明显这就是为了实现红黑树而设计的内部类。不过我们发现,TreeNode并不是直接继承Node,而是使用了LinkedHashMap中的Entry实现,它保存了前后节点的顺序(也就是我们的插入顺序)。
/** * HashMap.Node subclass for normal LinkedHashMap entries. */
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
LinkedHashMap是直接继承自HashMap,具有HashMap的全部性质,同时得益于每一个节点都是一个双向链表,保存了插入顺序,这样我们在遍历LinkedHashMap时,顺序就同我们的插入顺序一致。当然,也可以使用访问顺序,也就是说对于刚访问过的元素,会被排到最后一位。
public static void main(String[] args) {
//以访问顺序
LinkedHashMap<Integer, String> map = new LinkedHashMap<>(16, 0.75f, true);
map.put(1, "A");
map.put(2, "B");
map.put(3, "C");
map.get(2);
System.out.println(map);
}
观察结果,我们发现,刚访问的结果被排到了最后一位。
TreeMap
TreeMap其实就是自动维护顺序的一种Map,就和我们前面提到的TreeSet一样:
/** * The comparator used to maintain order in this tree map, or
* null if it uses the natural ordering of its keys.
* * @serial */
private final Comparator<? super K> comparator;private transient Entry<K,V> root;
/*** Node in the Tree. Doubles as a means to pass key-value pairs back to
* user (see Map.Entry).*/
static final class Entry<K,V> implements Map.Entry<K,V> {
我们发现它的内部直接维护了一个红黑树,就像它的名字一样,就是一个Tree,因为它默认就是有序的,所以说直接采用红黑树会更好。我们在创建时,直接给予一个比较规则即可。
Map的使用
我们首先来看看Map的一些基本操作:
public static void main(String[] args) {
Map<Integer, String> map = new HashMap<>();
map.put(1, "A");
map.put(2, "B");
map.put(3, "C");
System.out.println(map.get(1)); //获取Key为1的值
System.out.println(map.getOrDefault(0, "K")); //不存在就返回K
map.remove(1); //移除这个Key的键值对
}
由于Map并未实现迭代器接口,因此不支持foreach,但是JDK1.8为我们提供了forEach方法使用:
public static void main(String[] args) {
Map<Integer, String> map = new HashMap<>();
map.put(1, "A");
map.put(2, "B");
map.put(3, "C");
map.forEach((k, v) -> System.out.println(k+"->"+v));
//也可以获取所有的Entry来foreach
for (Map.Entry<Integer, String> entry : map.entrySet()) {
int key = entry.getKey();
String value = entry.getValue();
System.out.println(key+" -> "+value);
}
}
我们也可以单独获取所有的值或者是键:
public static void main(String[] args) {
Map<Integer, String> map = new HashMap<>();
map.put(1, "A");
map.put(2, "B");
map.put(3, "C");
System.out.println(map.keySet()); //直接获取所有的key
System.out.println(map.values()); //直接获取所有的值
}
再谈Set原理
观察HashSet的源码
发现HashSet几乎都在操作内部维护的一个HashMap,也就是说,HashSet只是一个表壳,而内部维护的HashMap才是灵魂!
// Dummy value to associate with an Object in the backing Map
private static final Object PRESENT = new Object();
可见,在添加元素时,其实添加的是一个键为我们插入的元素,而值就是PRESENT常量
/** * Adds the specified element to this set if it is not already present.
* More formally, adds the specified element e to this set if
* this set contains no element e2 such that
* (e==null ? e2==null : e.equals(e2)).
* If this set already contains the element, the call leaves the set
* unchanged and returns false.
* * @param e element to be added to this set
* @return true if this set did not already contain the specified
* element */
public boolean add(E e) {
return map.put(e, PRESENT)==null;
}
观察其他的方法,也几乎都是在用HashMap做事,所以说,HashSet利用了HashMap内部的数据结构,轻松地就实现了Set定义的全部功能!
再来看TreeSet,实际上用的就是TreeMap:
/** * The backing map. */
private transient NavigableMap<E,Object> m;
同理,这里就不多做阐述了。
JDK1.8新增方法使用
最后,我们再来看看JDK1.8中集合类新增的一些操作(之前没有提及的)首先来看看compute方法:
public static void main(String[] args) {
Map<Integer, String> map = new HashMap<>();
map.put(1, "A");
map.put(2, "B");
//compute会将指定Key的值进行重新计算,若Key不存在,v会返回null
map.compute(1, (k, v) -> {
return v+"M"; //这里返回原来的value+M
});
map.computeIfPresent(1, (k, v) -> { //当Key存在时存在则计算并赋予新的值
return v+"M"; //这里返回原来的value+M
});
System.out.println(map);
}
也可以使用computeIfAbsent,当不存在Key时,计算并将键值对放入Map
public static void main(String[] args) {
Map<Integer, String> map = new HashMap<>();
map.put(1, "A");
map.put(2, "B");
map.computeIfAbsent(0, (k) -> { //若不存在则计算并插入新的值
return "M"; //这里返回M
});
System.out.println(map);
}
merge方法用于处理数据:
public static void main(String[] args) {
List<Student> students = Arrays.asList(
new Student("yoni", "English", 80),
new Student("yoni", "Chiness", 98),
new Student("yoni", "Math", 95),
new Student("taohai.wang", "English", 50),
new Student("taohai.wang", "Chiness", 72),
new Student("taohai.wang", "Math", 41),
new Student("Seely", "English", 88),
new Student("Seely", "Chiness", 89),
new Student("Seely", "Math", 92) );
Map<String, Integer> scoreMap = new HashMap<>();
students.forEach(student -> scoreMap.merge(student.getName(), student.getScore(), Integer::sum));
scoreMap.forEach((k, v) -> System.out.println("key:" + k + "总分" + "value:" + v));
}
static class Student {
private final String name;
private final String type;
private final int score;
public Student(String name, String type, int score) {
this.name = name;
this.type = type;
this.score = score;
}
public String getName() {
return name;
}
public int getScore() {
return score;
}
public String getType() {
return type;
}
}
集合的嵌套
既然集合类型中的元素类型是泛型,那么能否嵌套存储呢?
public static void main(String[] args) {
Map<String, List<Integer>> map = new HashMap<>(); //每一个映射都是 字符串<->列表
map.put("卡布奇诺今犹在", new LinkedList<>());
map.put("不见当年倒茶人", new LinkedList<>());
System.out.println(map.keySet());
System.out.println(map.values());
}
通过Key获取到对应的值后,就是一个列表:
map.get("卡布奇诺今犹在").add(10);
System.out.println(map.get("卡布奇诺今犹在").get(0));
让套娃继续下去:
public static void main(String[] args) {
Map<Integer, Map<Integer, Map<Integer, String>>> map = new HashMap<>();
}
你也可以使用List来套娃别的:
public static void main(String[] args) {
List<Map<String, Set<String>>> list = new LinkedList<>();
}
流Stream和Optional的使用
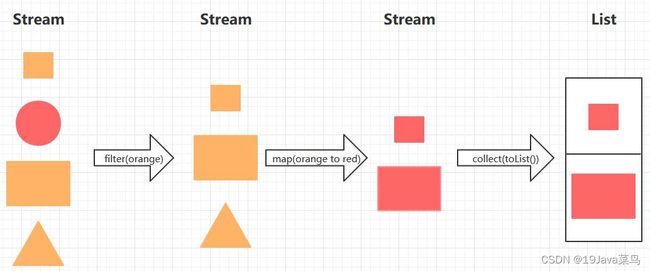
Java 8 API添加了一个新的抽象称为流Stream,可以让你以一种声明的方式处理数据。Stream 使用一种类似用 SQL 语句从数据库查询数据的直观方式来提供一种对 Java 集合运算和表达的高阶抽象。Stream API可以极大提高Java程序员的生产力,让程序员写出高效率、干净、简洁的代码。这种风格将要处理的元素集合看作一种流, 流在管道中传输, 并且可以在管道的节点上进行处理, 比如筛选, 排序,聚合等。元素流在管道中经过中间操作(intermediate operation)的处理,最后由最终操作(terminal operation)得到前面处理的结果。
它看起来就像一个工厂的流水线一样!我们就可以把一个Stream当做流水线处理:
public static void main(String[] args) {
List<String> list = new ArrayList<>();
list.add("A");
list.add("B");
list.add("C"); //移除为B的元素
Iterator<String> iterator = list.iterator();
while (iterator.hasNext()){
if(iterator.next().equals("B")) iterator.remove();
} //Stream操作
list = list //链式调用
.stream() //获取流
.filter(e -> !e.equals("B")) //只允许所有不是B的元素通过流水线
.collect(Collectors.toList()); //将流水线中的元素重新收集起来,变回List
System.out.println(list);
}
可能从上述例子中还不能感受到流处理带来的便捷,我们通过下面这个例子来感受一下:
public static void main(String[] args) {
List<Integer> list = new ArrayList<>();
list.add(1);
list.add(2);
list.add(3);
list.add(3);
list = list
.stream()
.distinct() //去重(使用equals判断)
.sorted((a, b) -> b - a) //进行倒序排列
.map(e -> e+1) //每个元素都要执行+1操作
.limit(2) //只放行前两个元素
.collect(Collectors.toList());
System.out.println(list);
}
当遇到大量的复杂操作时,我们就可以使用Stream来快速编写代码,这样不仅代码量大幅度减少,而且逻辑也更加清晰明了(如果你学习过SQL的话,你会发现它更像一个Sql语句)
注意:不能认为每一步是直接依次执行的!
List<Integer> list = new ArrayList<>();
list.add(1);
list.add(2);
list.add(3);
list.add(3);
//实际上,stream会先记录每一步操作,而不是直接开始执行内容,当整个链式调用完成后,才会依次进行!
list = list
.stream()
.distinct() //断点
.sorted((a, b) -> b - a)
.map(e -> {
System.out.println(">>> "+e); //断点
return e+1;
})
.limit(2) //断点
.collect(Collectors.toList());
接下来,我们用一堆随机数来进行更多流操作的演示:
public static void main(String[] args) {
Random random = new Random(); //Random是一个随机数工具类
random
.ints(-100, 100) //生成-100~100之间的,随机int型数字(本质上是一个IntStream)
.limit(10) //只获取前10个数字(这是一个无限制的流,如果不加以限制,将会无限进行下去!)
.filter(i -> i < 0) //只保留小于0的数字
.sorted() //默认从小到大排序
.forEach(System.out::println); //依次打印
}
我们可以生成一个统计实例来帮助我们快速进行统计:
public static void main(String[] args) {
Random random = new Random(); //Random是一个随机数工具类
IntSummaryStatistics statistics = random
.ints(0, 100)
.limit(100)
.summaryStatistics(); //获取语法统计实例
System.out.println(statistics.getMax()); //快速获取最大值
System.out.println(statistics.getCount()); //获取数量
System.out.println(statistics.getAverage()); //获取平均值
}
普通的List只需要一个方法就可以直接转换到方便好用的IntStream了:
public static void main(String[] args) {
List<Integer> list = new ArrayList<>();
list.add(1);
list.add(1);
list.add(2);
list.add(3);
list.add(4);
list.stream()
.mapToInt(i -> i) //将每一个元素映射为Integer类型(这里因为本来就是Integer)
.summaryStatistics();
}
还可以通过flat来对整个流进行进一步细分:
public static void main(String[] args) {
List<String> list = new ArrayList<>();
list.add("A,B");
list.add("C,D");
list.add("E,F"); //我们想让每一个元素通过,进行分割,变成独立的6个元素
list = list
.stream() //生成流
.flatMap(e -> Arrays.stream(e.split(","))) //分割字符串并生成新的流
.collect(Collectors.toList()); //汇成新的List
System.out.println(list); //得到结果
}
也可以只通过Stream来完成所有数字的和,使用reduce方法:
public static void main(String[] args) {
List<Integer> list = new ArrayList<>();
list.add(1);
list.add(2);
list.add(3);
int sum = list
.stream()
.reduce((a, b) -> a + b) //计算规则为:a是上一次计算的值,b是当前要计算的参数,这里是求和
.get(); //我们发现得到的是一个Optional类实例,不是我们返回的类型,通过get方法返回得到的值
System.out.println(sum);
}
通过上面的例子,我们发现,Stream不喜欢直接给我们返回一个结果,而是通过Optinal的方式,那么什么是Optional呢?
Optional类是Java8为了解决null值判断问题,使用Optional类可以避免显式的null值判断(null的防御性检查),避免null导致的NPE(NullPointerException)。总而言之,就是对控制的一个判断,为了避免空指针异常。
public static void main(String[] args) {
String str = null;
if(str != null){ //当str不为空时添加元素到List中
list.add(str);
}
}
有了Optional之后,我们就可以这样写:
public static void main(String[] args) {
String str = null;
Optional<String> optional = Optional.ofNullable(str); //转换为Optional
optional.ifPresent(System.out::println); //当存在时再执行方法
}
可以选择直接get或是当值为null时,获取备选值:
public static void main(String[] args) {
String str = null;
Optional optional = Optional.ofNullable(str); //转换为Optional(可空)
System.out.println(optional.orElse("lbwnb"));
// System.out.println(optional.get()); 这样会直接报错
}
同样的,Optional也支持过滤操作和映射操作,不过是对于单对象而言:
public static void main(String[] args) {
String str = "A";
Optional optional = Optional.ofNullable(str); //转换为Optional(可空)
System.out.println(optional.filter(s -> s.equals("B")).get()); //被过滤了,此时元素为null,获取时报错
}
public static void main(String[] args) {
List<String> list = new ArrayList<>();
String str = "A";
Optional optional = Optional.ofNullable(str); //转换为Optional(可空)
System.out.println(optional.map(s -> s + "A").get()); //在尾部追加一个A
}
其他操作自学了解。
Arrays和Collections的使用
Arrays是一个用于操作数组的工具类,它提供了大量的工具方法:
/**
* This class contains various methods for manipulating arrays (such as
* sorting and searching). This class also contains a static factory
* that allows arrays to be viewed as lists. <- 注意,这句话很关键
*
* @author Josh Bloch
* @author Neal Gafter
* @author John Rose
* @since 1.2
*/
public class Arrays {
由于操作数组并不像集合那样方便,因此JDK提供了Arrays类来增强对数组操作,比如:
public static void main(String[] args) {
int[] array = {1, 5, 2, 4, 7, 3, 6};
Arrays.sort(array); //直接进行排序(底层原理:进行判断,元素少使用插入排序,大量元素使用双轴快速/归并排序)
System.out.println(array); //由于int[]是一个对象类型,而数组默认是没有重写toString()方法,因此无法打印到想要的结果
System.out.println(Arrays.toString(array)); //我们可以使用Arrays.toString()来像集合一样直接打印每一个元素出来
}
public static void main(String[] args) {
int[] array = {1, 5, 2, 4, 7, 3, 6};
Arrays.sort(array);
System.out.println("排序后的结果:"+Arrays.toString(array));
System.out.println("目标元素3位置为:"+Arrays.binarySearch(array, 3)); //二分搜素,必须是已经排序好的数组!
}
public static void main(String[] args) {
int[] array = {1, 5, 2, 4, 7, 3, 6};
Arrays
.stream(array) //将数组转换为流进行操作
.sorted()
.forEach(System.out::println);
}
public static void main(String[] args) {
int[] array = {1, 5, 2, 4, 7, 3, 6};
int[] array2 = Arrays.copyOf(array, array.length); //复制一个一模一样的数组
System.out.println(Arrays.toString(array2));
System.out.println(Arrays.equals(array, array2)); //比较两个数组是否值相同
Arrays.fill(array, 0); //将数组的所有值全部填充为指定值
System.out.println(Arrays.toString(array));
Arrays.setAll(array2, i -> array2[i] + 2); //依次计算每一个元素(注意i是下标位置)
System.out.println(Arrays.toString(array2)); //这里计算让每个元素值+2
}
思考:当二维数组使用Arrays.equals()进行比较以及Arrays.toString()进行打印时,还会得到我们想要的结果吗?
public static void main(String[] args) {
Integer[][] array = {{1, 5}, {2, 4}, {7, 3}, {6}};
Integer[][] array2 = {{1, 5}, {2, 4}, {7, 3}, {6}};
System.out.println(Arrays.toString(array)); //这样还会得到我们想要的结果吗?
System.out.println(Arrays.equals(array2, array)); //这样还会得到true吗?
System.out.println(Arrays.deepToString(array)); //使用deepToString就能到打印多维数组
System.out.println(Arrays.deepEquals(array2, array)); //使用deepEquals就能比较多维数组
}
那么,一开始提到的当做List进行操作呢?
可以使用Arrays.asList()来将数组转换为一个 固定长度的List
public static void main(String[] args) {
Integer[] array = {1, 5, 2, 4, 7, 3, 6};
List<Integer> list = Arrays.asList(array); //不支持基本类型数组,必须是对象类型数组
Arrays.asList("A", "B", "C"); //也可以逐个添加,因为是可变参数
list.add(1); //此List实现是长度固定的,是Arrays内部单独实现的一个类型,因此不支持添加操作
list.remove(0); //同理,也不支持移除
list.set(0, 8); //直接设置指定下标的值就可以
list.sort(Comparator.reverseOrder()); //也可以执行排序操作
System.out.println(list); //也可以像List那样直接打印
}
变戏法:allows arrays to be viewed as lists,实际上只是当做List使用,本质还是数组
因此数组的属性依然存在!因此如果要将数组快速转换为实际的List,可以像这样:
public static void main(String[] args) {
Integer[] array = {1, 5, 2, 4, 7, 3, 6};
List<Integer> list = new ArrayList<>(Arrays.asList(array));
}
通过自行创建一个真正的ArrayList并在构造时将Arrays的List值传递。
既然数组操作都这么方便了,集合操作能不能也安排点高级的玩法呢?那必须的,JDK为我们准备的Collocations类就是专用于集合的工具类:
public static void main(String[] args) {
List<Integer> list = new ArrayList<>();
list.add(0);
list.add(1);
System.out.println(Collections.max(list));
System.out.println(Collections.min(list));
}
当然,Collections提供的内容相比Arrays会更多,希望大家下去自行了解,这里就不多做介绍了
集合类编程实战
- 反转链表
1 <- 3 <- 5 <- 7 <- 9 转换为 1 <- 3 <- 5 <- 7 <- 9
现在有一个单链表,尝试将其所有节点倒序排列
public class ListReverse {
public static void main(String[] args) {
Node node=new Node(1);
node.next=new Node(3);
node.next.next=new Node(5);
node.next.next.next=new Node(7);
node.next.next.next.next=new Node(9);
node=reverse(node);
while (node!=null){
System.out.print(node.data+" ");
node=node.next;
}
}
public static class Node{
public int data;
public Node next;
public Node(int data){
this.data=data;
}
}
public static Node reverse(Node node){
if (node.next==null) return node;
Node newNode=reverse(node.next);
Node next = node.next;
next.next=node;
node.next=null;
return newNode;
}
}
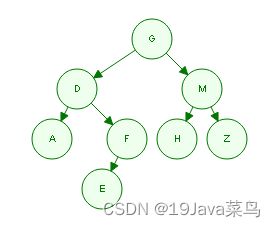
- 重建二叉树
现在知道二叉树的前序: GDAFEMHZ,以及中序: ADEFGHMZ,请根据已知信息还原这颗二叉树。
- 双栈计算器
实现一个计算器,要求输入一个计算公式(含加减乘除运算符,没有负数但是有小数),得到结果,比如输入:1+4*3/1.321,得到结果为:2.2
- KMP算法
现在给定一个主字符串和一个子字符串,请判断主字符串是否包含子字符串,例如
主字符串:ABCABCDHI,子字符串:ABCD,
因此主字符串包含此子字符串;
主字符串:ABCABCUISA,子字符串:ABCD,则不包含。