卡尔曼滤波与航迹融合
卡尔曼滤波与航迹融合
文章目录
- 卡尔曼滤波与航迹融合
- 前言
- 一、航迹数据仿真
- 二、卡尔曼滤波器
-
- 1.举例说明
- 2.卡尔曼滤波算法.
- 3.航迹融合
- 4.实验过程及结果
- 总结
- 代码
前言
这是我雷达信号处理课的一个作业,有些知识我也是新学的,原理也不是很懂.
所谓的航迹融合,就是将各传感器或者雷达扫描到的目标位置进行融合处理,使目标位置信息更加稳定可靠.
以下是本篇文章正文内容,下面案例可供参考
一、航迹数据仿真
在进行航迹融合之前,需要产生航迹数据,我们需要了解一些飞行物体的运动模型,常见的物体运动模型有:匀速模型,匀加速模型,转弯模型等.
先来了解一个最简单的匀速模型:
高中时我们就学过,物体进行匀速运动时的模型可以表示为:
![]()
这个数据用矩阵表示为:
![]()
然后写成下面的形式:
![]()
进一步我们用状态变量来表示:
![]()
在实际场景中,需要考虑外界干扰的影响,即

![]()
此时,观测模型可表示为:
![]()
更正一下,
二、卡尔曼滤波器
这里本来还有一步是航迹关联的,因为实际情况有可能观测到多个目标.但由于本次仿真是仿真一个目标的航迹数据,所以航迹关联这一步省略.以后如果有类似实验再进行补充.
1.举例说明
这里引用一位博主的例子:卡尔曼算法精讲与C++实现
在进行航迹融合前要对数据进行平滑处理,这里使用卡尔曼滤波器.
目标跟踪是卡尔曼滤波算法的一个重要应用,使用一系统列观测数据对位置,速度和加速度等信息进行估计.在滤波步骤中,卡尔曼滤波会先通过当前时刻的状态进行下一个更新时刻进行状态预测.预测估计系统包含了系统的不确定性,当获取到下一个量测后,通过加权平均对预测估计值进行更新,当量测值的不确定性越低时,在测量更新中的加权比重也就越高.
在这里,需要简单说一下卡尔曼滤波器.
这是一个在上述链接找到的例子,利用卡尔曼滤波器来估计室温.
现在的温度是25°C,需要估计出下一分钟的室内温度.
根据经验,室内的温度一般比较恒定,因此你对室下一分钟室温的估计值为25°C.但这个估计值仅仅是由经验估计出来的,所以它是有偏差的.因此这个值并不完全可信.然后我们假设这个偏差是由高斯白噪声造成的,并将其设为5°C.(5°C是这样来的,假设k-1时估计温度的最优偏差为3,你对自己的不确定度为4,这样可以得出32+42=52)
这时为了增加估计的准确度,我们需要借助其他方法来估计下一分钟的温度.没错,就是用温度计.我们假设从温度计获取下一分钟的室温为26°C,但这个温度也是不太确定的,假设偏差为4°.(其实我也不太明白为什么是这样的…)
于是,我们需要综合你的估计结果和温度计的测量结果来得出当前的温度.在现实生活中,我们是比较相信温度计的,因此温度估计应该更偏向温度计.这个判断依据是根它们的协方差来的.因为Kk=52/(52+42)=0.78,所以下一分钟的温度估计值是25+0.78*(26-25)=25.78.因此当前估计出的实际温度为25.78°C.
这时,我们已经得出k时刻的最优估计温度了,利用这个温度来继续估计k+1时刻的温度.在此之前,我们还要得出k时刻估计温度的最优估计偏差.这个值是这样来的, ( 1 − K k ) ∗ 5 2 = 2.35 \sqrt{(1-K_{k})*5^2}=2.35 (1−Kk)∗52=2.35,这个2.35是相对上面的3的.就这样,不断进行递归计算,从面预测最优估计值.
2.卡尔曼滤波算法.
卡尔曼滤波算法主要由5个公式组成,在此之前需要对其状态量初始化:
x ^ ( 0 ∣ 0 ) = E [ x ( 0 ) ] P ( 0 ∣ 0 ) = E [ ( x ( 0 ) − x ^ ( 0 ∣ 0 ) ) ( x ( 0 ) − x ^ ( 0 ∣ 0 ) ) T ] \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \hat{x}(0|0)=E[x(0)]\\ \quad\quad\quad\quad\quad P(0|0)=E[(x(0)-\hat{x}(0|0))(x(0)-\hat{x}(0|0))^{T}] x^(0∣0)=E[x(0)]P(0∣0)=E[(x(0)−x^(0∣0))(x(0)−x^(0∣0))T]
1.时间更新:
x ^ k ∣ k − 1 = E ( x k ∣ Z k − 1 ) = F k − 1 x ^ k − 1 ∣ k − 1 \quad\quad\quad\quad\quad\hat{x}_{k|k-1}=E(x_{k}|Z^{k-1})=F_{k-1}\hat{x}_{k-1|k-1} x^k∣k−1=E(xk∣Zk−1)=Fk−1x^k−1∣k−1
P k ∣ k − 1 = c o v ( x ~ k ∣ k − 1 ) = F k − 1 P k − 1 ∣ k − 1 F k − 1 T + G k − 1 Q k − 1 G k − 1 T \quad\quad\quad\quad\quad P_{k|k-1}=cov(\tilde{x}_{k|k-1})=F_{k-1}P_{k-1|k-1}F^{T}_{k-1}+G_{k-1}Q_{k-1}G^{T}_{k-1} Pk∣k−1=cov(x~k∣k−1)=Fk−1Pk−1∣k−1Fk−1T+Gk−1Qk−1Gk−1T
2.量测更新:
在获取新的量测值后,更新滤波增益方程,并对一步预测结果进行更新:
K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 \quad\quad\quad\quad\quad K_k=P_{k|k-1}H^T_k(H_kP_{k|k-1}H^T_k+R_k)^{-1} Kk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1
状态和协方差更新方程:
x ^ k ∣ k = E ( X k ∣ Z k ) = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) P k ∣ k = c o v ( x ^ k ∣ k ) = [ I − K k H k ] P k ∣ k − 1 \quad\quad\quad\quad\quad\hat{x}_{k|k}=E(X_k|Z^k)=\hat{x}_{k|k-1}+K_k(z_k-H_k\hat{x}_{k|k-1})\\ \quad\quad\quad\quad\quad P_{k|k}=cov(\hat{x}_{k|k})=[I-K_kH_k]P_{k|k-1} x^k∣k=E(Xk∣Zk)=x^k∣k−1+Kk(zk−Hkx^k∣k−1)Pk∣k=cov(x^k∣k)=[I−KkHk]Pk∣k−1
3.航迹融合
分布式航迹融合中利用数据融合算法对来自同一目标的局航迹进行融合处理,最终形成新的精确度最高的系统航迹.
1.凸组合融合算法:
这是一种常用的融合算法.若所有传感器估计误差之间互不相关,则融合方程为:
{ X ^ = [ ∑ i = 1 N ( P i ) − 1 ] − 1 ∑ i = 1 N ( P i ) − 1 X ^ i P − 1 = ∑ i = 1 N ( P i ) − 1 ] − 1 \left\{\begin{matrix}\hat{X}=[\sum_{i=1}^{N}(P^i)^{-1}]^{-1}\sum_{i=1}^{N}(P^i)^{-1}\hat{X}^i \\ P^{-1}=\sum_{i=1}^{N}(P^i)^{-1}]^{-1} \end{matrix}\right. {X^=[∑i=1N(Pi)−1]−1∑i=1N(Pi)−1X^iP−1=∑i=1N(Pi)−1]−1
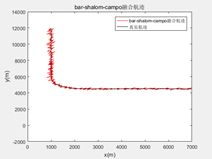
2.Bar-Shalom-Campo融合算法
当系统存在噪声时,可使用Bar-Shalom-Campo融合算法进行航迹融合,其融合方程和误差协方差阵分别为:
{ x ^ = x ^ i + ( P i − P i j ) ( P i + P j − P i j − P j i ) − 1 ( x ^ j − x ^ i ) P = P i + ( P i − P i j ) ( P i + P j − P i j − P j i ) − 1 ( P i − P j i ) \left\{\begin{matrix}\hat{x}=\hat{x}^i+(P^i-P^{ij})(P^i+P^j-P^{ij}-P{ji})^{-1}(\hat{x}^j-\hat{x}^i) \\ P=P^i+(P^i-P^{ij})(P^i+P^j-P^{ij}-P{ji})^{-1}(P^i-P^{ji}) \end{matrix}\right. {x^=x^i+(Pi−Pij)(Pi+Pj−Pij−Pji)−1(x^j−x^i)P=Pi+(Pi−Pij)(Pi+Pj−Pij−Pji)−1(Pi−Pji)
4.实验过程及结果
本次实验采用两种典型的航路进行仿真,利用滤波结果直接进行航迹融合处理,运用以上两种融合算法进行融合.并通过原始航迹和融合航迹的对比来比较两种融合算法的实用性:
(1)匀速目标飞行
目标的起始位置为(1000m,12000m),以(15m/s,-5m/s)的速度匀速飞行,且融合中心的采样周期为2s.仿真结果如图1~图5所示





(2) 转弯模型
目标的起始位置为(1000m,12000m),开始以(1m/s,-15m/s)的速度匀速飞行,且融合中心的采样周期为2s,在T=402s的时候以抛物线的形式转弯,之后进行匀速直线运动,.仿真结果如图6~图10所示
总结
从实验结果来看, 通过对以上三种典型航迹的仿真将航迹融合后的X轴、Y轴的误差均方差进行对比,在不考虑不同传感器的同一个目标的航迹估计误差之间相关性的情况下,简单凸组合航迹融合算法是最优的。
代码
代码可参考此链接:
航迹融合算法MATLAB仿真程序