【论文精读】KD-MVS
今天读的是发表在ECCV2022上的自监督MVS文章,作者来自于旷视科技和清华大学。
文章链接:arxiv
代码链接:https://github.com/megvii-research/KD-MVS
目录
- Abstract
- 1. Introduction
- 2. Related work
- 3. Methodology
-
- 3.1 Self-supervised Teacher Training
- 3.2 Distillation-based Student Training
-
- Pseudo Probabilistic Knowledge Generation
- Student Training
- 4. Experiments
-
- 4.1 Datasets
- 4.2 Implementation Details
- 4.3 Experimental Results
- 4.4 Ablation Study
- 5. Discussion
-
- 5.1 Insights of Effectiveness
- 5.2 Comparisons to SOTA Methods
- 5.3 Limitations
- 6. Conclusion
Abstract
监督多视图立体 (MVS) 方法在重建质量方面取得了显着进步,但面临收集大规模地面实况深度的挑战。 在本文中,我们提出了一种基于知识蒸馏的新型 MVS 自监督训练管道,称为 KD-MVS,主要包括自监督教师培训和基于蒸馏的学生培训。 具体来说,教师模型使用光度和特征一致性以自我监督的方式进行训练。 然后我们通过概率知识转移将教师模型的知识提炼到学生模型。 在经过验证的知识的监督下,学生模型能够大大优于其教师。 在多个数据集上进行的大量实验表明我们的方法甚至可以胜过监督方法。
1. Introduction
介绍了MVS相关内容。
主要贡献如下:
- 提出了一种基于知识蒸馏的名为 KD-MVS 的新型自监督训练pipeline。
- 设计了一个内部特征度量一致性损失来对教师模型进行稳健的自我监督训练。
- 建议进行知识蒸馏,将经过验证的知识从自我监督的教师转移到学生模型中,以提高表现。
- 该方法在 Tanks and Temples、DTU 和 BlendedMVS数据集上实现了SOTA。
2. Related work
介绍了learning-based MVS(包括有监督和自监督)和知识蒸馏。
3. Methodology
在本节中,我们详细阐述了如图 2 所示的框架。KD-MVS 主要包括自我监督的教师培训(第 3.1 节)和基于蒸馏的学生培训(第 3.2 节)。 具体来说,我们首先使用参考视图和重建视图之间的 photometric and featuremetric consistency,以自我监督的方式训练教师模型。 然后,我们通过交叉视图检查和概率编码生成教师模型的伪概率分布。 在伪概率的监督下,学生模型以离线蒸馏方式进行蒸馏损失训练。 值得注意的是,所提出的 KD-MVS 是用于训练 MVS 网络的通用管道,它可以很容易地适应任意基于学习的 MVS 网络。 本文主要研究KD-MVS与CasMVSNet。
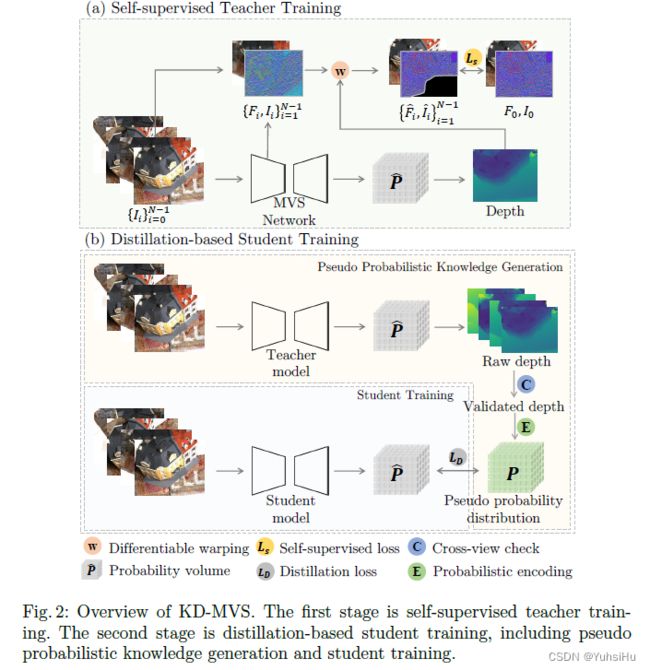
3.1 Self-supervised Teacher Training
除了自监督 MVS 中使用的传统光度一致性外,我们还建议使用内部特征和特征一致性作为额外的监督信号。 光度和特征一致性都是通过计算参考视图和重建视图之间的距离获得的。
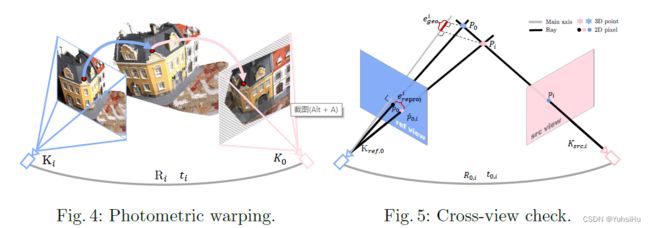
View Construction介绍了形如CasMVSNet的视图重建过程,写了一遍homography warping的公式(如图4)。
Loss Formulation介绍了损失函数。自监督训练损失由两部分组成:photometric loss光度损失 L p h o t o L_{photo} Lphoto 和featuremetric loss特征损失 L f e a L_{fea} Lfea。 L p h o t o L_{photo} Lphoto 基于原始RGB参考图像和重建图像之间的L1距离。 然而,我们发现光度损失对光照条件和拍摄角度敏感,导致预测的完整性较差。 为了克服这个问题,我们使用特征度量损失来构建更稳健的损失函数。给定从 MVS 网络的特征网中提取的特征 { F i } i = 0 N − 1 \{F_{i}\}^{N−1}_{i=0} {Fi}i=0N−1,以及从第 i i i 个视图生成的重构特征图 F i ^ \hat{F_{i}} Fi^,我们的 F i ^ \hat{F_{i}} Fi^ 和 F 0 F_{0} F0 之间的特征度量损失为:

值得注意的是,我们提出使用在线训练 MVS 网络的内部特征网提取的内部特征而不是外部特征(例如,由预训练的主干网络提取)来计算特征度量损失。 我们的见解是,MVS 的本质是沿极线的多视图特征匹配,因此这些特征应该具有局部判别性。 预训练的骨干网络,例如 ResNet 和 VGGNet 通常使用图像分类损失进行训练,因此它们的特征不是局部判别性的。 如图 3 所示,我们比较了在线自监督训练期间由外部预训练主干网(ResNet)和 MVS 网络的内部编码器提取的特征。 这两个选项导致完全不同的特征表示,我们在 Sec 4.4 中通过实验对其进行了研究。
总而言之,自监督教师培训的最终损失函数是:
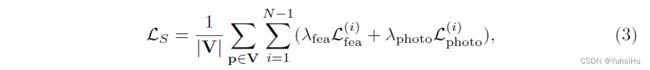
其中 V 是图像像素的有效子集。 λ f e a λ_{fea} λfea 和 λ p h o t o λ_{photo} λphoto 是两个手动调整的权重,在我们的实验中,我们分别将它们设置为 4 4 4 和 1 1 1。 对于从粗到精的网络,例如 CasMVSNet,损失函数应用于每个正则化步骤。

3.2 Distillation-based Student Training
为了进一步激发自监督 MVS 网络的潜力,我们采用知识蒸馏的思想,将教师的概率知识转移到学生模型中。 这个过程主要包括两个步骤,即伪概率知识生成和学生训练。
Pseudo Probabilistic Knowledge Generation
我们认为知识转移是通过概率分布完成的。 然而,在 MVS 中应用蒸馏时,我们面临两个主要问题。 (a) 教师模型生成的原始每视图深度包含大量异常值,这不利于训练学生模型。 所以,我们执行交叉视图检查以过滤异常值。 (b) 教师模型的真实概率知识不能直接用于训练学生模型。 这是因为从粗到细的MVS网络中的深度假设需要根据前一阶段的结果动态采样,我们不能保证教师模型和学生模型总是共享相同的深度假设。 为了解决这个问题,我们通过概率编码生成伪概率分布。
Cross-view Check 用于过滤原始深度图中的异常值,这些异常值是由自监督教师模型在未标记的训练数据上推断出来的。 自然地,教师模型的输出是每个视图的深度图和相应的置信度图。 对于从粗到精的方法,例如 CasMVSNet,我们将所有三个阶段的置信度图相乘以获得最终的置信度图,并将最高分辨率的深度图作为最终的深度预测。
我们将参考视图的最终置信度图表示为 C 0 C_{0} C0,将最终深度预测表示为 D 0 D_{0} D0,将源视图的深度图表示为 { D i } i = 1 N − 1 \{D_{i}\}^{N−1}_{i=1} {Di}i=1N−1。如图5所示,考虑参考图像坐标中的任意像素 p 0 p_{0} p0,我们将 2D 点 p 0 p_{0} p0 转换为具有深度值 D 0 ( p 0 ) D_{0}(p_{0}) D0(p0) 的 3D 点 P 0 P_{0} P0。 然后我们将 P 0 P_{0} P0 反投影到第 i i i 个源视图并获得源视图中的点 p i p_{i} pi。 使用其估计的深度 D i ( p i ) D_{i}(p_{i}) Di(pi),我们可以将 p i p_{i} pi 投射到 3D 点 P i P_{i} Pi。 最后,我们将 P i P_{i} Pi 投影到参考视图并得到 p ^ 0 , i \hat{p}_{0,i} p^0,i。 然后 p 0 p_{0} p0 处的重投影误差可以写为 e r e p r o j i = ∣ ∣ p 0 − p ^ 0 , i ∣ ∣ e^{i}_{reproj} = \vert{}\vert{}p_{0}−\hat{p}_{0,i}\vert{}\vert{} ereproji=∣∣p0−p^0,i∣∣。 还定义了几何误差 e g e o i e^{i}_{geo} egeoi 来测量从参考相机观察到的 P 0 P_{0} P0 和 P i P_{i} Pi 的相对深度误差, e g e o i = ∥ D ^ 0 ( P 0 ) − D ^ 0 ( P i ) ∥ / D 0 ( P 0 ) e^{i}_{geo} =∥\hat{D}_{0}(P_{0}) − \hat{D}_{0}(P_{i})∥/D_{0}(P_{0}) egeoi=∥D^0(P0)−D^0(Pi)∥/D0(P0),其中 D ^ 0 ( P 0 ) \hat{D}_{0}(P_{0}) D^0(P0) 和 D ^ 0 ( P i ) \hat{D}_{0}(P_{i}) D^0(Pi) 是参考视图中 P 0 P_{0} P0 和 P i P_{i} Pi 的投影深度。因此,关于第 i i i 个源视图的有效像素子集定义为:

其中 τ τ τ表示阈值,我们将 τ c o n f τ_{conf} τconf、 τ r e p r o j τ_{reproj} τreproj和 τ g e o τ_{geo} τgeo分别设置为0.15、1.0和0.01。 最终经过验证的掩码是 N − 1 N-1 N−1 个源视图中所有 p 0 i {p_{0}}_{i} p0i 的交集。 获得的 { D ^ 0 ( P i ) } i = 0 N − 1 \{\hat{D}_{0}(P_{i})\}^{N−1}_{i=0} {D^0(Pi)}i=0N−1 和经过验证的mask 将进一步用于生成伪概率分布。
Probabilistic Encoding 使用 { D ~ 0 ( P i ) } i = 0 N − 1 \{\widetilde{D}_{0}(Pi)\}^{N−1}_{i=0} {D 0(Pi)}i=0N−1 为参考视图中的每个有效像素 p 0 p_{0} p0 生成深度值 d d d 的伪概率分布 P p 0 ( d ) P_{p_{0}} (d) Pp0(d)。我们将 P p 0 P_{p_{0}} Pp0建模为平均深度值为 μ ( p 0 ) μ(p_{0}) μ(p0)、方差为 σ 2 ( p 0 ) σ^{2}(p_{0}) σ2(p0)的高斯分布,可以通过最大似然估计得到:

μ ( p 0 ) μ(p_{0}) μ(p0) 融合了来自多个视图的深度信息,而 σ 2 ( p 0 ) σ^{2}(p_{0}) σ2(p0) 反映了教师模型在 p 0 p_{0} p0 处的不确定性,这将为蒸馏训练期间的学生模型提供概率知识。
Student Training
使用伪概率分布 P P P,我们能够通过强制其预测概率分布 P ^ \hat{P} P^ 与 P P P 相似来从头开始训练学生模型。对于离散深度假设 { d k } k = 0 D \{d_{k}\}^{D}_{k=0} {dk}k=0D,我们获得它们的伪概率 { P ( d k ) } k = 0 D \{P(d_{k})\}^{D}_{k=0} {P(dk)}k=0D 在连续概率分布 P P P 上使用 SoftMax 对 { P ( d k ) } k = 0 D \{P(d_{k})\}^{D}_{k=0} {P(dk)}k=0D 进行归一化,将结果作为最终的离散伪概率值。 我们使用KL散度来衡量学生模型的预测概率与伪概率之间的距离。 蒸馏损失 L D L_{D} LD 定义为:
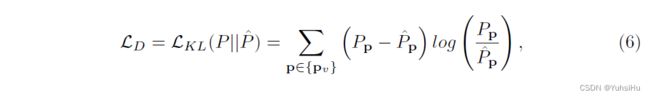
其中 { p v } \{p_{v}\} {pv} 表示交叉视图检查后有效像素的子集。
在实验中,我们发现经过训练的学生模型也有可能成为一名教师,并将其知识进一步提炼给另一个学生模型。 作为训练时间和性能之间的权衡,我们再次执行知识蒸馏过程。
4. Experiments
4.1 Datasets
介绍了数据集。
4.2 Implementation Details
介绍了一些参数设置。
4.3 Experimental Results
介绍了实验结果。
4.4 Ablation Study
对内部特征loss进行了消融。
对自训练参数进行了解释。
5. Discussion
5.1 Insights of Effectiveness
5.2 Comparisons to SOTA Methods
5.3 Limitations
- 伪概率分布的质量在很大程度上取决于交叉视图检查阶段,需要仔细调整相关的超参数。
- 知识蒸馏是data-hungry的,它可能无法像预期的那样使用相对较小的数据集。
6. Conclusion
复述了一下贡献。