Leetcode刷题总结(三)
1、不用加号的加法
class Solution {
public:
int add(int a, int b) {
int sum=0;
int carry = 0;
while(b!=0) // 当进位为0,说明计算结束
{
sum = a ^ b; // 异或计算未进位部分
carry = (uint32_t)(a & b) << 1; // 与计算进位部分,进位必须是无符号数
a = sum; // 保存未进位部分
b = carry; // 保存进位部分
}
return a;
}
};
2、最长单词
思路:注意题目说的是,该单词由其他单词组合而成,因此不一定是两个单词组合,可能是多个单词组合,那么需要不断递归下去。如果当前字符串中长度为len的子串,出现在单词哈希表中,那么就去掉这一子串,接着递归剩余串能否在单词哈希表中找到。由于可能重复使用单词,因此单词哈希表不做删除。
class Solution {
public:
bool iscompose(string word, unordered_set & tmp)
{
if(word.size()==0) // 如果字符串为空,那肯定能组合
{
return true;
}
for(int i=1;i<=word.size();i++) // 由于word中是被不知长度的若干子串组合,因此这里枚举子串的长度。
{
if(tmp.count(word.substr(0, i)) && iscompose(word.substr(i), tmp)) // 第一个判断条件是找到第一个子串,那么第二个条件就是递归剩余子串能否在哈希表中找到
{
return true;
}
}
return false;
}
string longestWord(vector& words) {
if(words.size()==0)
{
return "";
}
string ans="";
unordered_set mp(words.begin(), words.end()); // 构建单词哈希表
for(int i=0;i tmp = mp;
tmp.erase(word); // 自己不能组合自己,因此在哈希表中先删除自己
if(iscompose(word, tmp)) // 如果在哈希表中发现,这个单词能够被组合,那就判断长度
{
if(word.size()>ans.size())
{
ans = word;
}else if(word.size()==ans.size())
{
ans = min(word, ans);
}
}
}
return ans;
}
};
3、计算器

思路: 这里没有要求括号,并且都是非负整数,因此可以直接遍历字符串,然后遇到运算符就处理,维护一个数字栈,将数字入栈.
class Solution {
public:
void trim(string & s)
{
int index = 0;
if(!s.empty())
{
while( (index = s.find(' ',index)) != string::npos)
{
s.erase(index,1);
}
}
}
stack s_num;
int calculate(string s) {
trim(s); // 去除字符串中的所有空格
int num=0;
char c = '+'; // 可以视为表达式: 0 + 表达式,这样不改变值,而第一个运算符是+
for(int i=0;i<=s.size();i++) // 这里可以取到i=s.size(),是因为字符串末尾是'\0',如果不遍历到最后的话,会漏掉最后一个运算数字
{
if(isdigit(s[i]))
{
num = num*10 + (s[i] - '0');
}else{
if(c=='+'){ // 遇到+、-先不运算,直接入栈
s_num.push(num);
}else if(c=='-'){
s_num.push(-num);
}else if(c=='*'){ // 遇到*、/ 要运算完再入栈
int tmp = s_num.top();
s_num.pop();
num *= tmp;
s_num.push(num);
}else{
int tmp = s_num.top();
s_num.pop();
num = tmp / num;
s_num.push(num);
}
num=0;
c = s[i];
}
}
int ans=0;
while(s_num.size()){ // 栈里面的数字,直接相加,没有乘除法
ans+=s_num.top();
s_num.pop();
}
return ans;
}
};
4、字母与数字

思路:数组只存放字母和数字,而要找子数组里面包含字母和数字的个数相同(不考虑字母、数字的长度),因此可以将数字看成1,字母看成-1,计算前缀和.
对于前缀和, 有两种情况:
- prefix[i]=0, 说明 0~i 的长度是包含字母和数字个数相同的子数组;
- 如果遇到prefix[i]==prefix[j] , 也就是相同前缀和, 那么意味着 i~j 这个区间内存在包含字母和数字个数相同的子数组.(因为相同前缀和, 意味着区间内数字有变大或变小, 但最终回到起始, 说明区间内不管怎么变, 总增量为0)
class Solution {
public:
vector findLongestSubarray(vector& array) {
int n=array.size();
vector prefix(n,0);
unordered_map M; //key,left_index
int left=0,right=-1;
for(int i=0;i='A' && ch<='z') prefix[i]=-1;
else prefix[i]=1;
}
// 计算前缀和
for(int i=1;isecond){ // 不是第一次遇到这个前缀和, 那就将当前下标和最左端的下标 长度进行比较
right=i;left=it->second+1;
}
}
}
// 给出结果
vector ans;
for(int i=left;i<=right;++i) ans.push_back(array[i]);
return ans;
}
};
5、2出现的次数

思路:直接暴力肯定超时. 需要分别统计数字中每一位数字能出现2的次数,而在看每一位数字时,要考虑其前缀、后缀.
class Solution {
public:
int numberOf2sInRange(int n) {
long ans=0;
long base = 1; // 基底
int prex = n/10; // 前缀
int lastx = n%10; // 看每一位数字
int post=0; // 后缀
while(n!=post) // 当后缀和原来一样大时,说明已经遍历完了
{
if(lastx>2) // 如果当前数字大于2, 那么2必然出现, 前缀有多大, 就会出现多少次2. 因此统计次数为: 0~pre, 共pre+1次, 再乘上基底.
{
ans+=(prex+1)*base;
}else if(lastx==2){ // 如果刚好等于2, 那么不管数字出现多少, 都会被统计
ans+= prex*base + post + 1;
}else{
ans+= prex * base; // 如果小于2, 那么只考虑前缀出现的次数
}
post += lastx*base;
lastx = prex%10;
prex = prex/10;
base*=10;
}
return ans;
}
};
6、婴儿名字
思路: 用哈希表来统计名字和对应的次数, 但是这里有含义相同的名字, 需要进行归类. 这里采用并查集的思想, 每个名字都保留其父亲名字(实质上是含义相同且字典序最小), 这样每个名字都有对应, 记录在另一个哈希表中. 最后遍历名字和对应的次数即可.
class Solution {
public:
unordered_map name2num;
unordered_map parent; // 保存
string find(string s)
{
if(parent.count(s)==0)
return s;
string root = find(parent[s]);
parent[s] = root;
return root;
}
void m_union(string s1, string s2)
{
s1 = find(s1);
s2 = find(s2);
if(s1!=s2)
{
if(s1 trulyMostPopular(vector& names, vector& synonyms) {
for(auto name : synonyms)
{
int pos = name.find(',');
string n1 = name.substr(1, pos - 1);
string n2 = name.substr(pos + 1, name.size() - pos - 2);
m_union(n1,n2);
}
for(auto name : names)
{
int pos = name.find('(');
string nm = name.substr(0, pos);
int ifre = stoi(name.substr(pos + 1, name.size() - pos - 2));
name2num[find(nm)] += ifre;
}
vector result;
for (auto& name : name2num)
{
string fre = to_string(name.second);
result.push_back(name.first + "(" + fre + ")");
}
return result;
}
};
7、主要元素
思路: 超过一半的元素, 其实是众数. 可以通过投票法来找到众数, 但是这里可能不存在, 而投票法的前提是众数一定存在, 因此投票完后要再验证一次是否满足条件.

根据主要元素的定义,主要元素的出现次数大于其他元素的出现次数之和,因此在遍历过程中,主要元素和其他元素两两抵消,最后一定剩下至少一个主要元素,此时 candidate为主要元素,且 count≥1.
class Solution {
public:
int majorityElement(vector& nums) {
int piao=0;
int pepole = nums[0];
for(int i=0;inums.size()/2)
{
return pepole;
}else{
return -1;
}
}
};
8、拿出最少的魔法豆(第280场周赛,超时)

思路: (1) 由于只拿出豆子, 不放回豆子, 因此数量必然是减少的. 又因为剩余非空袋子的豆子数量相同, 因此拿走豆子数量=总和-每袋豆子数量*袋数.
(2) 要使拿掉豆子的数量最少, 那先对数组排序, 从最少的豆子开始拿.
(3) 遍历数组, 考虑第 i 个位置, 基于(2), 0 ~ i-1 位置的豆子都要拿完, 而后面的袋子豆子数需要都等于x. 那这个x 最大值只能取beans[i], 如果比当前位置的豆子更多, 那么当前位置不能算入袋子, 必须拿空, 这样豆子被拿掉的数量更多了.
class Solution {
public:
long long minimumRemoval(vector& beans) {
if(beans.size()==1)
{
return 0;
}
int len = beans.size();
sort(beans.begin(), beans.end());
long long sum=0;
for(int i=0;i 9、马戏团人塔(超时)

思路: 第一次用动态规划解,超时了. 看了题解, 用贪心 + 二分来做.
class Solution {
public:
int bestSeqAtIndex(vector& height, vector& weight) {
if(height.size()==0)
{
return 0;
}
vector > man;
for(int i=0;i & a, const pair &b){
if(a.first==b.first)
{
return a.second>b.second;
}else{
return a.first res;
res.push_back(man[0].second); // 第一个人的体重可以直接加入
for(int i=1;i res.back()) // 如果当前的体重比数组末尾的人更大, 可以直接加入, 满足条件(因为身高是升序, 必然满足)
{
res.push_back(man[i].second);
}else{ // 如果当前体重更小, 而之前排序是按身高升序, 身高相同再体重降序, 体重更小说明身高相同. 那就从数组中找到恰好大于等于当前体重的人(此人身高和当前的身高相同), 进行体重的替换(换上了体重更小的人). 这样体现了贪心思想, 使体重更紧凑, 可以尽可能加入更多的人.
int index = lower_bound(res.begin(), res.end(), man[i].second) - res.begin();
res[index] = man[i].second;
}
}
return res.size();
}
};
10、骑士在棋盘上的概率(dfs超时)

思路: 定义dp[step][i][j]表示从(i, j)出发走了step步后还停留在棋盘上的概率。当(i,j)不在棋盘上时,dp[step][i][j]=0;当(i,j)在棋盘上且step=0时,dp[step][i][j]=1。而其他情况,dp[step][i][j] += dp[step - 1][ni][nj] / 8,是由上一步的8种情况统计得到概率。
class Solution {
public:
vector> dirs = {{-2, -1}, {-2, 1}, {2, -1}, {2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}};
double knightProbability(int n, int k, int row, int column) {
vector>> dp(k + 1, vector>(n, vector(n)));
for (int step = 0; step <= k; step++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (step == 0) {
dp[step][i][j] = 1;
} else {
for (auto & dir : dirs) {
int ni = i + dir[0], nj = j + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
dp[step][i][j] += dp[step - 1][ni][nj] / 8;
}
}
}
}
}
}
return dp[k][row][column];
}
};
11、最短超串(不会)
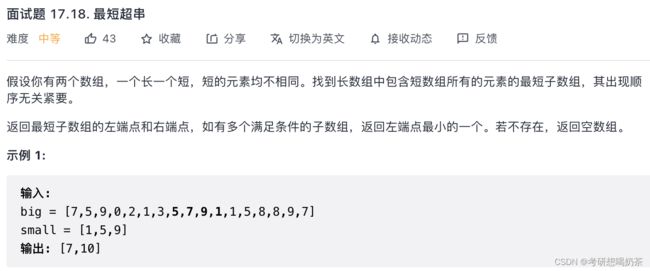
思路:遇到满足什么什么条件的连续区间问题,可以考虑用滑动窗口来解决。
滑动窗口的解题步骤:
1)先初始化l=0,r=0。
2)然后不断将右指针右移进行遍历,此时滑动窗口相应发生变化。
3)当区间满足条件后,再将左指针右移进行收缩区间,最终找到最短的满足条件的连续区间。
class Solution {
public:
vector shortestSeq(vector& big, vector& small) {
unordered_map need;
for(int i=0;i res;
for(;r=0) // 如果当前右指针的数字是small中需要的数字,并且该数字的出现次数还有多余,则diff--,表示要找的数字数量变少了
{
diff--;
}
while(diff==0) // diff==0 表示数字都被滑动窗口找到了,即当前窗口满足条件
{
if(r - l < min_len) // 比较窗口大小
{
min_len = r - l;
res = {l, r};
}
if(need.find(big[l])!=need.end() && ++need[big[l]]>0) // 如果左指针的数字是small中的数字,并且假设左指针右移后该数字的出现次数>0了,说明当前窗口已经不再满足条件,因为漏了一个数字出去。因此diff++,表示要找的数字数量变多了。
{
diff++;
}
l++; // 将左指针右移,进行区间的收缩
}
}
return res;
}
};
12、煎饼排序(不会)
思路:从arr.size()大小开始遍历,每次找当前数组里的最大值,然后通过两次翻转将最大值放到当前数组的尾部;而随着数组长度的缩减,每次都能将最大值排到末尾,最后当数组长度=1时,已经有序了。
class Solution {
public:
vector pancakeSort(vector& arr) {
vector ans;
int len = arr.size();
for(int i=len;i>1;i--)
{
int index = max_element(arr.begin(), arr.begin()+i) - arr.begin(); // 找当前长度为 i 的情况下,数组最大值
if(index==i-1) // 如果最大值的索引已经在尾部,那就不用动
{
continue;
}
reverse(arr.begin(), arr.begin()+index+1); // 进行这样两次翻转
reverse(arr.begin(), arr.begin() + i);
ans.push_back(index+1);
ans.push_back(i);
}
return ans;
}
};
13、最大子矩阵(不会)
class Solution {
public:
vector getMaxMatrix(vector>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vector b(n, 0); // 记录的是,矩形中每一列的元素和。这样就把求二维矩阵的和,转化成求b的子序列和。
vector ans(4, 0);
int max_sum = INT_MIN;
int ans_r1=0;
int ans_c1=0;
int sum=0;
for(int i=0;i0)
{
sum+=b[k];
}else{
sum = b[k];
ans_r1 = i;
ans_c1 = k;
}
if(sum>max_sum)
{
max_sum = sum;
ans[0] = ans_r1;
ans[1] = ans_c1;
ans[2] = j;
ans[3] = k;
}
}
}
}
return ans;
}
};
14、元素和为目标值的子矩阵数量
思路:这题和上一题可以采用相同的降维方法,定义每一列的和。然后进行全局遍历,只要和等于目标值就++。思路比较简单。
class Solution {
public:
int numSubmatrixSumTarget(vector>& matrix, int target) {
int ans=0;
int sum=0;
int m = matrix.size();
int n = matrix[0].size();
vector b(n, 0); // 记录每一列的和
for(int i=0;i 15、二叉搜索树序列
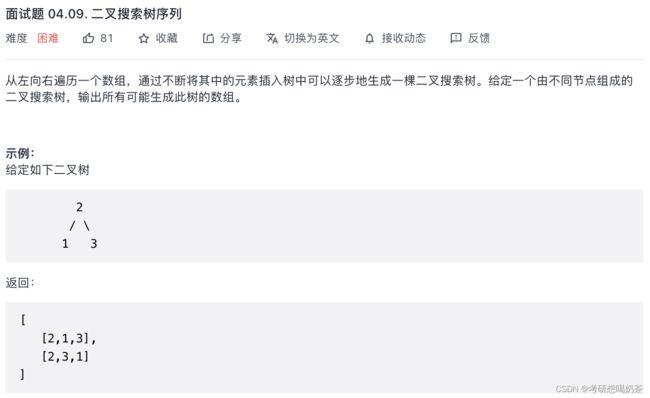
思路:其实这题意思是要遍历二叉搜索树的所有可能性,

以这个为例:
1)路径的第一个元素必然是根节点12,而下一个元素的选择必然是5或19,和顺序无关;
2)假设选了5,当前路径为【12,5】,那么接下来可以选的是2、9、19,也同样和顺序无关;
3)后续同理,直到没有可选的节点了,就是一个完整的路径。
因此这里是回溯的做法,可以定义一个队列来保存之后可选择的节点,如果队列为空意味着没得选,那就路径完成。
而在(1)中,给出了5、19两种选择,因此假设当前选了5进入下一层递归,那么当递归结束返回时(准备选19),要将5再加入队列,此时路径也要去掉最后一个元素(也就是5),这样就把5留在下一层递归中去选择。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector > ans;
vector path; // 保存当前路径
void dfs(deque& q)
{
if(q.empty()) // 已经没得选了,那就已经得到了完整路径
{
ans.push_back(path);
return;
}
for(int i=0;ival); // 选了当前节点,然后下面分别把左右孩子入队(这是下一层递归中的可选节点)
if(node->left)
{
q.push_back(node->left);
}
if(node->right)
{
q.push_back(node->right);
}
dfs(q); // 进行下一层递归
// 递归结束,这时候要消除当前节点的影响,就剔除左右孩子入队的情况
if(node->left)
{
q.pop_back();
}
if(node->right)
{
q.pop_back();
}
q.push_back(node); // 当前节点要再次入队,例如原来是【5,19】,现在递归选过5后,要变成【19,5】,下次选19
path.pop_back(); // 同时路径也要剔除5
}
}
vector> BSTSequences(TreeNode* root) {
if(root==NULL)
{
return {{}};
}
deque q; // 定义双端队列,来保留下一个候选的节点
q.push_back(root); // 第一个候选节点肯定是根节点
dfs(q);
return ans;
}
};
回溯模版:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素) {
处理结点;
backtracking(路径,选择列表)); // 递归
回溯,撤销处理结果;
}
}
作者:dong-men
链接:https://leetcode-cn.com/problems/bst-sequences-lcci/solution/pei-tu-hui-su-mo-ban-xiang-xi-zhu-shi-by-dong-men/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
16、布尔运算(不会)
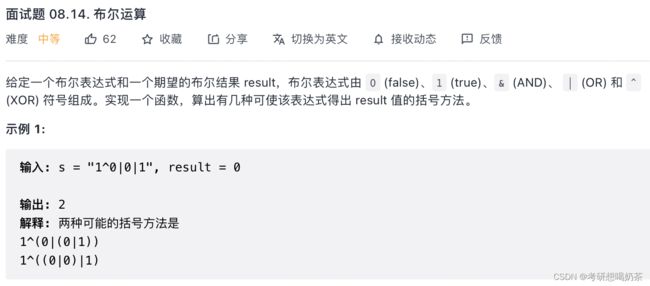
思路:区间dp的做法,定义一个三维的dp数组。
dp[i][j][0]代表第i个字符到第j个字符,result=0的可能性个数。
dp[i][j][1]代表第i个字符到第j个字符,result=1的可能性个数。
class Solution {
public:
int countEval(string s, int result) {
int n = s.size();
vector > > dp(n, vector > (n, vector(2,0)));
// 初始化,只有一个字母的情况
for(int i=0;i 17、最大黑方阵(只会暴力枚举)

思路:动态规划,cnt[r][c][0/1]分别保存(r,c)右侧、下侧连续的黑色像素的个数。
class Solution {
public:
vector findSquare(vector>& matrix) {
vector ans(3, 0);
int n = matrix.size();
if(n == 0) return {};
if(n == 1){
if(matrix[0][0] == 0)
return {0, 0, 1};
else
return {};
}
//cnt[r][c][0/1],0右侧,1下侧
vector>> cnt(n, vector>(n, vector(2)));
for(int r = n-1; r >= 0; r--){ // 要从方阵右下角开始遍历,因为这样才能让索引小的cnt保存到后面的值
for(int c = n-1; c >= 0; c--){
if(matrix[r][c] == 1)
cnt[r][c][0] = cnt[r][c][1] = 0;
else{
//统计cnt[r][c][0/1]
if(r < n-1) cnt[r][c][1] = cnt[r+1][c][1] + 1;
else cnt[r][c][1] = 1;
if(c < n-1) cnt[r][c][0] = cnt[r][c+1][0] + 1;
else cnt[r][c][0] = 1;
//更新当前最大子方阵
int len = min(cnt[r][c][0], cnt[r][c][1]);//最大的可能的边长,要取短边,不然不能构成方阵
while(len >= ans[2]){//要答案r,c最小,所以带等号
if(cnt[r+len-1][c][0] >= len && cnt[r][c+len-1][1] >= len){ // 再看看另外两条边是否满足长度,注意题目只要求4条边均为黑色,而不是整个方阵都是黑色
//可以构成长为len的方阵
ans = {r, c, len};
break;
}
len--;
}
}
}
}
return ans;
}
};
18、三数之和(超时)
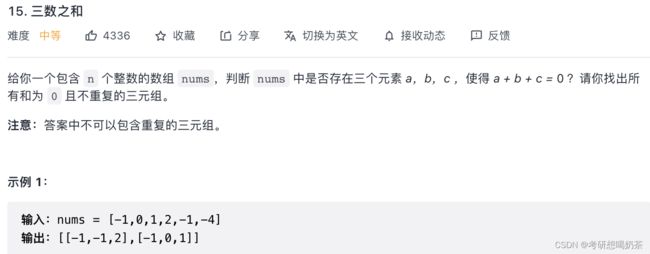
思路:基本思路是三重循环,而题目要求不重复的三元组,因此要考虑去重。
1)对数组先排序,这样就避免获得重复的三元组,要保证a<=b<=c。
2)排序后,相邻元素可能是相同的,这也要避免。
例如-1,0,1,1
先选了第一个1,但是下次遍历可能又选到第二个1,组成了相同的三元组。
// 伪代码
nums.sort()
for first = 0 .. n-1
// 只有和上一次枚举的元素不相同,我们才会进行枚举
if first == 0 or nums[first] != nums[first-1] then
for second = first+1 .. n-1
if second == first+1 or nums[second] != nums[second-1] then
for third = second+1 .. n-1
if third == second+1 or nums[third] != nums[third-1] then
// 判断是否有 a+b+c==0
check(first, second, third)
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/3sum/solution/san-shu-zhi-he-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3)在从小到大遍历b的时候,要从大到小遍历c。因为假设a+b1+c1=0,那下一个b2>b1,因此若存在a+b2+c2=0,c2一定小于c1,也就是左侧。
class Solution {
public:
vector> threeSum(vector& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
vector> ans;
// 枚举 a
for (int first = 0; first < n; ++first) {
// 需要和上一次枚举的数不相同
if (first > 0 && nums[first] == nums[first - 1]) {
continue;
}
// c 对应的指针初始指向数组的最右端
int third = n - 1;
int target = -nums[first]; // 此时题目变为了两数之和=target,可以用双指针来使时间复杂度从O(n2)降为O(n)
// 枚举 b
for (int second = first + 1; second < n; ++second) {
// 需要和上一次枚举的数不相同
if (second > first + 1 && nums[second] == nums[second - 1]) {
continue;
}
// 需要保证 b 的指针在 c 的指针的左侧
while (second < third && nums[second] + nums[third] > target) {
--third;
}
// 如果指针重合,随着 b 后续的增加
// 就不会有满足 a+b+c=0 并且 b 19、组合

思路:有1~n个数,要选其中k个数。其实就是回溯的思维,遍历每个数的时候有选、不选两种情况,进行分别的回溯即可。
class Solution {
public:
vector > ans;
vector tmp;
void dfs(int cur, int n, int k)
{
// 剪枝。当前已经遍历到cur位置,如果已有的数量tmp.size + 剩余的数字数量,还小于k。说明就算把剩余的数字全选上也不能满足k个数字的要求,因此可以提前返回。
if(tmp.size() + (n - cur + 1) < k)
{
return;
}
if(tmp.size()==k)
{
ans.push_back(tmp);
return;
}
// 选取当前的cur
tmp.push_back(cur);
dfs(cur+1, n, k);
// 回溯状态
tmp.pop_back();
// 不选当前的cur,那就直接进入下一个状态cur+1
dfs(cur+1, n, k);
}
vector> combine(int n, int k) {
dfs(1, n, k);
return ans;
}
};
20、下一个排列 (不会)

思路:题目要找下一个序列,这个序列要是字典序刚好更大一点的序列,如果当前序列已经是字典序最大序列(降序排列),那么下一个序列是字典序最小的序列(升序排列)。
1、首先要从后往前遍历,找到第一个i 且 nums[i]

class Solution {
public:
void nextPermutation(vector& nums) {
int i=nums.size()-2;
while(i>=0 && nums[i]>=nums[i+1])
{
i--;
}
if(i>=0)
{
int j=nums.size()-1;
while(j>=0 && nums[j]<=nums[i])
{
j--;
}
swap(nums[i], nums[j]); // 找到比 i 更大的第一个数,交换之后,整个序列比原始序列更大了
reverse(nums.begin()+i+1, nums.end()); // 使后面从小到大排列,使序列变化幅度最小
}else{ // 说明此时是完全倒序(字典序最大),直接翻转整个数组即得到字典序最小的序列
reverse(nums.begin(), nums.end());
}
}
};
21、Z字形变换

思路:直接模拟可行,就是比较复杂。而题解中有一种巧妙的思路,用一个标志位来判断当前遍历是从上往下,还是从下往上。
class Solution {
public:
string convert(string s, int numRows) {
if(numRows<2)
{
return s;
}
vector vec(numRows, ""); // 定义每一行的字符串
int i=0;
int flag=-1; // 正向取、反向取的标记,控制了Z字形读取的顺序
for(int k=0;k 22、适合打劫银行的日子
思路:这种前后都要判断的,可以先遍历数组,把前后的情况都保存下来(这里是动态规划预处理),再进行比较。设left数组,left[i]表示i之前非递减的天数;设right数组同理。
class Solution {
public:
vector<int> goodDaysToRobBank(vector<int>& security, int time) {
int n = security.size();
vector<int> left(n, 0);
vector<int> right(n, 0);
for(int i=1;i<n-1;i++)
{
if(security[i]<=security[i-1])
{
left[i] = left[i-1]+1;
}
if(security[n-i-1]<=security[n-i])
{
right[n-i-1] = right[n-i]+1;
}
}
vector<int> ans;
for(int i=time;i<n-time;i++)
{
if(left[i]>=time && right[i]>=time)
{
ans.push_back(i);
}
}
return ans;
}
};
23、最长回文子串

思路1 : 中心扩展的方法,遍历每个位置,然后以该位置为回文子串的中心点向左右两边扩展,直到不构成回文串为止。
class Solution {
public:
pair<int, int> expand(string s, int left, int right)
{
while(left>=0&&right<s.size() && s[left]==s[right])
{
left--;
right++;
}
return {left+1, right-1};
}
string longestPalindrome(string s) {
int start=0;
int end=0;
int max_len=1;
for(int i=0;i<s.size();i++)
{
auto [left1, right1] = expand(s, i, i); // 中心点可能是单独的
auto [left2, right2] = expand(s, i, i+1); // 中心点可能是两个点 如 abba
if(right1 - left1 + 1>max_len)
{
start = left1;
end = right1;
max_len = right1 - left1+1;
}
if(right2 - left2 + 1>max_len)
{
start = left2;
end = right2;
max_len = right2 - left2+1;
}
}
return s.substr(start, max_len);
}
};
思路2: 动态规划,设dp[i][j]表示i~j内是回文子串。
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if(n<2)
{
return s;
}
vector<vector<int> > dp(n, vector<int>(n, 0));
for(int i=0;i<n;i++)
{
dp[i][i]=1; // 单个字符当然能构成回文
}
int start=0;
int max_len = 1;
for(int len=2;len<=n;len++) // 回文子串的长度从2开始
{
for(int i=0;i<n;i++) // 枚举左边界
{
int j = i+len-1; // 右边界
if(j>=n) // 超出边界
{
break;
}
if(s[i]!=s[j]) // 左右边界不相等,那么肯定不是回文
{
dp[i][j]=0;
}else{
if(j-i<3) // 当长度不超过3,说明是回文
{
dp[i][j]=1;
}else{ // 超过3,要取决于内部是不是回文
dp[i][j]=dp[i+1][j-1];
}
}
if(dp[i][j] && j-i+1>max_len)
{
max_len = j-i+1;
start=i;
}
}
}
return s.substr(start, max_len);
}
};