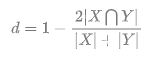医学图像分割之 Dice Loss

医学图像分割之 Dice Loss

在很多关于医学图像分割的竞赛、论文和项目中，发现 Dice 系数(Dice coefficient) 损失函数出现的频率较多，自己也存在关于分割中 Dice Loss 和交叉熵损失函数(cross-entropy loss) 的一些疑问，这里简单整理.

1. Dice coefficient 定义
   Dice系数 - 维基百科

Dice系数, 根据 Lee Raymond Dice[1] 命名，是一种集合相似度度量函数，通常用于计算两个样本的相似度(值范围为 [0, 1])：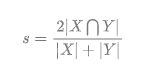

• X 和 Y 之间的交集； 和 分别表示 X 和 Y 的元素个数. 其中，分子中的系数 2，是因为分母存在重复计算 X 和 Y 之间的共同元素的原因.

语义分割问题而言，X - GT 分割图像, Y - Pred 分割图像.

Dice 系数差异函数(Dice loss)：

1.1. Dice 系数计算示例
医学图像分割常用的损失函数

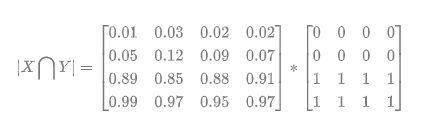
预测的分割图的 dice 系数计算，首先将 近似为预测图与 GT 分割图之间的点乘，并将点乘的元素结果相加：

[1] - Pred 预测分割图与 GT 分割图的点乘：

[2] - 逐元素相乘的结果元素的相加和：

对于二分类问题，GT 分割图是只有 0, 1 两个值的，因此 可以有效的将在 Pred 分割图中未在 GT 分割图中激活的所有像素清零. 对于激活的像素，主要是惩罚低置信度的预测，较高值会得到更好的 Dice 系数.

关于 和 的量化计算，可采用直接简单的元素相加；也有采用取元素平方求和的做法：

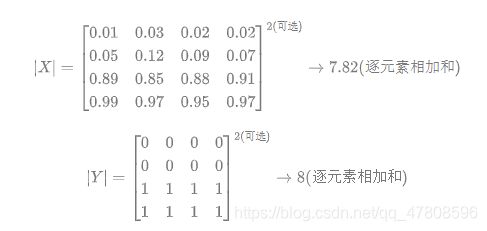
注：dice loss 比较适用于样本极度不均的情况，一般的情况下，使用 dice loss 会对反向传播造成不利的影响，容易使训练变得不稳定.

1.2. Dice-coefficient loss function vs cross-entropy
这是在 stackexchange.com 上一个提问：

Dice-coefficient loss function vs cross-entropy

问题：

在训练像素分割的神经网络时，如 FCN，如何选择交叉熵损失函数还是 Dice-coefficient 损失函数？

回答：

采用交叉熵损失函数，而非 dice-coefficient 和类似 IoU 度量的损失函数，一个令人信服的愿意是其梯度形式更优(the gradients are nicer.)

交叉熵损失函数中交叉熵值关于 logits 的梯度计算形式类似于 ，其中， 是 softmax 输出； 为 target.

而关于 dice-coefficient 的可微形式，loss 值为 或 ，其关于 的梯度形式是比较复杂的： 或 . 极端场景下，当 和 的值都非常小时，计算得到的梯度值可能会非常大. 通常情况下，可能导致训练更加不稳定.

直接采用 dice-coefficient 或者 IoU 作为损失函数的原因，是因为分割的真实目标就是最大化 dice-coefficient 和 IoU 度量. 而交叉熵仅是一种代理形式，利用其在 BP 中易于最大化优化的特点.

另外，Dice-coefficient 对于类别不均衡问题，效果可能更优. 然而，类别不均衡往往可以通过简单的对于每一个类别赋予不同的 loss 因子，以使得网络能够针对性的处理某个类别出现比较频繁的情况. 因此，对于 Dice-coefficient 是否真的适用于类别不均衡场景，还有待探讨.

机器学习 - 交叉熵Cross Entropy - AIUAI

2. Dice 系数的 Pytorch 实现
   2.1. Dice 系数

https://github.com/pytorch/pytorch/issues/1249

def dice_coeff(pred, target):
smooth = 1.
num = pred.size(0)
m1 = pred.view(num, -1) # Flatten
m2 = target.view(num, -1) # Flatten
intersection = (m1 * m2).sum()

return (2. * intersection + smooth) / (m1.sum() + m2.sum() + smooth)

2.2. Dice Loss
import torch.nn as nn
import torch.nn.functional as F

class SoftDiceLoss(nn.Module):
def init(self, weight=None, size_average=True):
super(SoftDiceLoss, self).init()

def forward(self, logits, targets):
    num = targets.size(0)
    smooth = 1
    
    probs = F.sigmoid(logits)
    m1 = probs.view(num, -1)
    m2 = targets.view(num, -1)
    intersection = (m1 * m2)

    score = 2. * (intersection.sum(1) + smooth) / (m1.sum(1) + m2.sum(1) + smooth)
    score = 1 - score.sum() / num
    return score

2.3. BCELoss2d
import torch.nn as nn
import torch.nn.functional as F

class BCELoss2d(nn.Module):
def init(self, weight=None, size_average=True):
super(BCELoss2d, self).init()
self.bce_loss = nn.BCELoss(weight, size_average)

def forward(self, logits, targets):
    probs = F.sigmoid(logits)  # 二分类问题，sigmoid等价于softmax
    probs_flat = probs.view(-1)
    targets_flat = targets.view(-1)
    return self.bce_loss(probs_flat, targets_flat)

3. Dice 系数的 Keras 实现
   From:Dice’s coefficient 　实现

smooth = 1. # 用于防止分母为0.
def dice_coef(y_true, y_pred):
y_true_f = K.flatten(y_true) # 将 y_true 拉伸为一维.
y_pred_f = K.flatten(y_pred)
intersection = K.sum(y_true_f * y_pred_f)
return (2. * intersection + smooth) / (K.sum(y_true_f * y_true_f) + K.sum(y_pred_f * y_pred_f) + smooth)

def dice_coef_loss(y_true, y_pred):
return 1. - dice_coef(y_true, y_pred)
4. Dice 系数的 TensorFlow 实现
def dice_coe(output, target, loss_type=‘jaccard’, axis=(1, 2, 3), smooth=1e-5):
“”"
Soft dice (Sørensen or Jaccard) coefficient for comparing the similarity of two batch of data,
usually be used for binary image segmentation
i.e. labels are binary.
The coefficient between 0 to 1, 1 means totally match.

Parameters
-----------
output : Tensor
    A distribution with shape: [batch_size, ....], (any dimensions).
target : Tensor
    The target distribution, format the same with `output`.
loss_type : str
    ``jaccard`` or ``sorensen``, default is ``jaccard``.
axis : tuple of int
    All dimensions are reduced, default ``[1,2,3]``.
smooth : float
    This small value will be added to the numerator and denominator.
        - If both output and target are empty, it makes sure dice is 1.
        - If either output or target are empty (all pixels are background), dice = ```smooth/(small_value + smooth)``, then if smooth is very small, dice close to 0 (even the image values lower than the threshold), so in this case, higher smooth can have a higher dice.

Examples
---------
>>> outputs = tl.act.pixel_wise_softmax(network.outputs)
>>> dice_loss = 1 - tl.cost.dice_coe(outputs, y_)

References
-----------
- `Wiki-Dice `__

"""
inse = tf.reduce_sum(output * target, axis=axis)
if loss_type == 'jaccard':
    l = tf.reduce_sum(output * output, axis=axis)
    r = tf.reduce_sum(target * target, axis=axis)
elif loss_type == 'sorensen':
    l = tf.reduce_sum(output, axis=axis)
    r = tf.reduce_sum(target, axis=axis)
else:
    raise Exception("Unknow loss_type")
dice = (2. * inse + smooth) / (l + r + smooth)
dice = tf.reduce_mean(dice)
return dice

5. Related
   [1] - 图像分割结果的评估—DICE参数