JS算法探险之队列(Queue)
❝乔布斯经常说到一句话:“Stay hungry, Stay foolish”
❞
- 「Stay hungry」:永不满足,
- 「Stay foolish」: 是说埋头做自己的事,不要理会前行路上的各种嘲讽声音。
大家好,我是「柒八九」。
今天,我们继续探索JS算法相关的知识点。我们来谈谈关于队列 Queue的相关知识点和具体的算法。
如果,想了解其他数据结构的算法介绍,可以参考我们已经发布的文章。如下是算法系列的往期文章。
文章list
- 整数
- 常规排序算法
- 数组
- 字符串
- 链表
- 栈
你能所学到的知识点
❝❞
- JS队列的各种实现
- 滑动窗口的概念和对应算法
- 利用队列解决和二叉树层树相关的算法
文章概要
- 知识点简讲
- 滑动窗口
- 二叉树的广度优先搜索(BFS)
知识点简讲
队列是个啥
队列是一种遵从「先进先出」(FIFO)原则的「有序集合」。队列在尾部添加新元素,并从顶部移除元素。「最新添加的元素必须排在队列的末尾」。

在现实中,最常见的队列的例子就是排队。

JS版本的Queue
由于JS语言的特殊性,不存在真正意义上的Queue结构,一般使用数组特定的Api(push/shift)模拟最简单的queue使得能够满足「先进先出」的特性。
let queue = [];
queue.push(1);
queue.push(2);
==== 入队 1、2====
queue.shift() // 1出队
queue.shift() // 2出队
在一些简单的场景下,利用数组来模拟队列是可以满足条件的。但是作为一个功能完备的数据结构,还有一些其他的功能,使用上述的实现方式显的有点捉襟见肘。
「这里做一个简单的补充」:其实针对stack/queue的实现方式有两种,一种是利用数组实现一个存储地址连续的结构,另外一种实现方式是利用链表实现存储地址不连续的结构。
那么,我们就自己实现一个比较功能完备的queue。它有如下的功能点
-
enqueue(element(s)):向队列 「尾部」添加一个(或多个)新的项。 -
dequeue():移除队列的第一项(即排在队列最前面的项)并返回被移除的元素。 -
peek():返回队列中第一个元素——最先被添加,也将是最先被移除的元素。队列不做任何变动(不移除元素,只返回元素信息——与Stack类的peek方法非常类似)。 -
isEmpty():如果队列中不包含任何元素,返回true,否则返回false。 -
size():返回队列包含的元素个数,与数组的length属性类似。
数组版本
class Queue {
constructor() {
this.items = [];
}
// 入队
enqueue(element) {
this.items.push(element);
}
// 出队,并返回队首元素
dequeue() {
return this.items.shift();
}
// 查看,队首元素
peek() {
return this.items[0]
}
// 如果队列里没有任何元素就返回`true`,否则返回`false`
isEmpty() {
return this.items.length === 0;
}
// 返回队列的元素个数
size() {
return this.items.length;
}
// 移除队列里所有的元素
clear() {
this.items = [];
}
}
上面是使用数组来实现queue,能够实现基本的CRUD。但是,如果还记得我们在介绍stack的时候,也利用数组实现了一个Stack。
下面是用数组实现stack和queue的具体代码。可以发现,在利用数组实现这两个数据结构时候,除了针对「剔除/查看」数据有点不同,其他方法都一模一样。(除去方法名的差异) 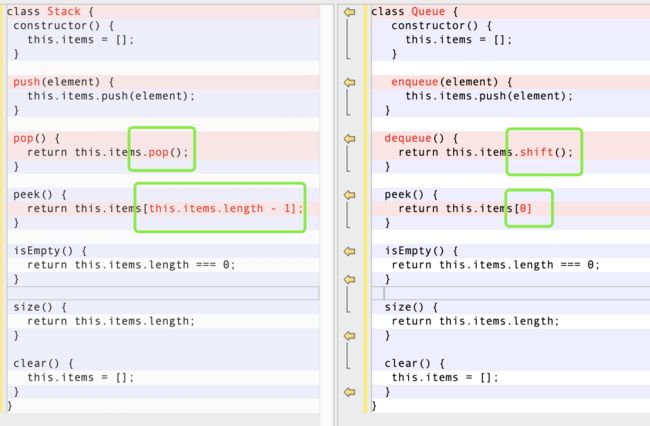
在针对一些不强调消耗和性能的情况下,用数组实现queue是一个不错且简单的方式。但是,由于queue删除数据的位置是在队首。在利用数组实现的queue中,每次删除一个元素,数组剩余的元素的序号地址,都需要进行变更。这样会造成不必要的性能损耗。
所以,大部分情况下,queue是利用链表构建的。
链表版本
这里再做一个简单说明,在js中,对象类型数据,它本身就是一个以零散方式存储的。我们来简单做一个实验。
class TestObject {
constructor() {
this.elements = {
o1:{},
o2:{},
};
}
}
let to = new TestObject()
我们利用Memory获取了,此时内存信息。我们特意查看了TestObject中elements发现,针对他两个属性o1/o2所存的数据都放在不同的内存地址上。
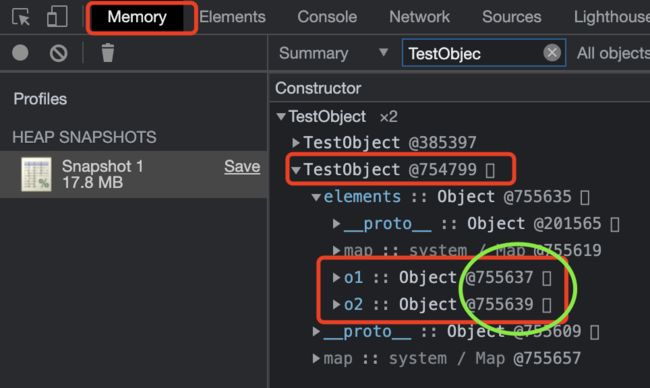
我们可以使用对象来存储元素信息。这样,就不需要「额外」的构建链表节点。
class Queue {
constructor() {
this.elements = {};
this.head = 0;
this.tail = 0;
}
enqueue(element) {
this.elements[this.tail] = element;
this.tail++;
}
dequeue() {
const item = this.elements[this.head];
delete this.elements[this.head];
this.head++;
return item;
}
peek() {
return this.elements[this.head];
}
size() {
return this.tail - this.head;
}
isEmpty() {
return this.tail - this.head === 0;
}
}
滑动窗口
在数组中某一个长度的「子数组」可以看成数组的一个「窗口」。若给定数组[1,2,3,4,5,6],那么子数组[2,3,4]就是其中一个大小为3的窗口。窗口向右滑动一个数字,那么窗口就包含数字[3,4,5]。
也就是向右滑动窗口,每向右滑动一个数字,都在窗口的「最右边」插入一个数字,同时把「最左边」的数字删除。即满足队列 「先进先出」的特性。
滑动窗口的平均值
题目描述:
❝给定一个「整数数据流」和一个「窗口大小」,根据该滑动窗口的大小,计算滑动窗口里所有数字的平均值。
❞
- 该类型的构造函数的参数确定滑动窗口的大小
- 每次调用
next函数,会在滑动窗口中添加一个整数,并返回滑动窗口的所有数字的平均值
分析
- 在窗口中添加数字,当窗口中的数字的数目超过限制时,还可以从窗口中删除数字。
- 例如,当窗口的大小为3,在添加第四个数字时,就需要从窗口中删除 「最早添加」进来的数字。
- 这是一种 「先进先出」的顺序,对应的数据容器为 「队列」
- 每次在窗口中添加数字之后,需要判断是否超出窗口的大小限制。如果超出限制,从队列中删除一个数字
- 利用
sum实时记录,窗口中 「现存数据」的和
代码实现
class MovingAverage {
constructor(size) {
this.nums = new Queue();
this.capacity = size;
this.sum = 0;
}
next(val) {
this.nums.enqueue(val);
this.sum+=val;
if(this.nums.size()>this.capacity){
this.sum -=this.nums.dequeue();
}
return this.sum / this.nums.size()
}
}
二叉树的广度优先搜索(BFS)
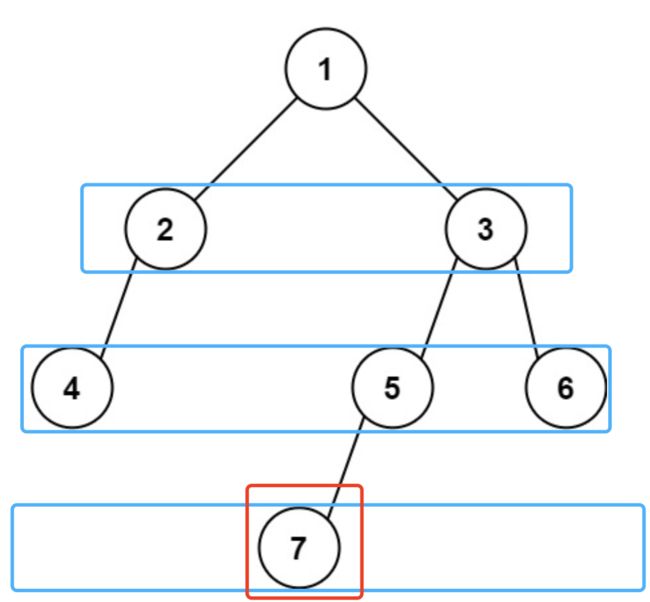
二叉树的广度优先搜索是从上到下「按层」遍历二叉树,从二叉树的根节点开始,先遍历二叉树的第一层,再遍历第二层,以此类推。
通常「基于队列来实现二叉树的广度优先搜索」。
- 从二叉树的根节点开始,先把根节点放入到一个队列中,然后 每次从队列中取出一个节点遍历。
- 如果该节点有左右子节点,则分别将它们添加到队列中。(先左后右)
- 以此类推,直到所有节点都被遍历
「二叉树节点」
class TreeNode {
val: number
left: TreeNode | null
right: TreeNode | null
constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
this.val = (val===undefined ? 0 : val)
this.left = (left===undefined ? null : left)
this.right = (right===undefined ? null : right)
}
}
利用queue实现「二叉树广度优先遍历」
function bfs(root){
let queue = new Queue();
if(root!=null) {
queue.enqueue(root);
}
let result = [];
while(!queue.isEmpty()){
let node = queue.dequeue();
result.push(node.val)
if(node.left!=null){
queue.enqueue(node.left);
}
if(node.right!=null){
queue.enqueue(node.right);
}
}
return result;
}
由于queue的「先进先出」特性,二叉树的「某一层节点按照从左到右的顺序」插入队列中。因此,这些节点一定会按照从左到右的顺序遍历到。用广度优先(BFS)的顺序遍历二叉树,很容易知道
- 「每层」最左边或者最右边的节点
- 「每层」的最大值或者最小值
也就是说,关于二叉树的题目如果出现「层」的概念,尝试用广度优先来解决问题。
二叉树中每层的最大值
题目描述:
❝输入一课二叉树,请找出二叉树中「每层」的最大值。
❞
示例:输入: root = [1,3,2,5,3,null,9] 输出: [1,3,9]
用一个队列实现二叉树的广度优先搜索
分析
- 找出二叉树中 「每层」的最大值,在遍历的时需要知道每层什么时候开始,什么时候结束。
- 因为,在某个时刻,队列中可能存在位于不同层的节点,如果不做区分的话,是无法获取到某层数据的最大值
- 解决上述问题的一个办法就是 「计数」
- 用两个变量分别记录两层节点的数目
- 变量
current记录当前遍历这一层中位于队列之中节点的数量 - 变量
next记录下一层中位于队列之中节点的数量
- 最开始把根节点插入队列中,把变量
current初始化为1.- 逐个从队列中取出节点遍历
- 每当从队列中 「取出一个节点」时, 「当前层的剩余节点数」就少一个,即
current - 1 - 当前遍历的节点有子节点,将子节点插入队列中,此时变量
next的数目增加1即next + 1
- 当
current的数值变成0时,表示当前层的所有节点都已经遍历完。、- 此时,可以通过比较当前层的所有节点的值,找出最大值
- 在开始遍历下一层节点之前
- 需要把
current的值设为next的值 - 变量
next重新初始化为0
- 需要把
代码实现
function largestValues(root) {
let current = 0;
let next = 0;
let queue = new Queue();
let result = [];
if(root!=null){
queue.enqueue(root);
current++;
}
let max = Number.MIN_SAFE_INTEGER;
while(!queue.isEmpty()){
let node = queue.dequeue();
current--;
max = Math.max(max,node.val);
if(node.left!=null){
queue.enqueue(node.left);
next++;
}
if(node.right !=null){
queue.enqueue(node.right);
next++;
}
if(current==0){
result.push(max);
max = Number.MIN_SAFE_INTEGER;
current = next;
next = 0;
}
}
return result;
}
用两个队列实现二叉树的广度优先搜索
分析
- 利用一个队列区分不同的层,需要用到两个变量
current/next,我们可以换一个思路。将不同层树的节点,存入不同的队列中。-
queue1只放当前遍历层的节点 -
queue2只放下一层的节点
-
- 最开始时,把二叉树的根节点放入队列
queue1中。- 接下来,每次从队列中取出一个节点遍历
- 队列
queue1用来存放当前遍历层的节点,总是从队列queue1中取出节点来遍历 - 如果当前遍历的节点有子节点,并且子节点位于下一层,则把子节点放入队列
queue2
- 当队列
queue1被清空时,此时能够获取到当前层的最大值 - 在开始遍历下一层之前,
- 把队列
queue1指向queue2 - 将队列
queue2重新初始化为空队列
- 把队列
代码实现
function largestValues(root) {
let q1 = new Queue();
let q2 = new Queue();
let result = [];
if(root!=null){
q1.enqueue(root);
}
let max = Number.MIN_SAFE_INTEGER;
while(!q1.isEmpty()){
let node = q1.dequeue();
max = Math.max(max,node.val);
if(node.left!=null){
q2.enqueue(node.left);
}
if(node.right !=null){
q2.enqueue(node.right);
}
if(q1.isEmpty()){
result.push(max);
max = Number.MIN_SAFE_INTEGER;
q1 = q2;
q2 = new Queue();
}
}
return result;
}
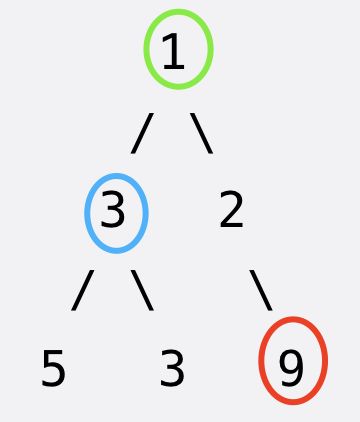
二叉树最底层最左边的值
题目描述:
❝输入一课二叉树,找出它「最底层最左边」节点的值。
❞
示例:输入: root = [1,2,3,4,null,5,6,null,null,7] 输出: 7
分析
- 题目越短,越需要咬文嚼字。
- 二叉树
- 最底层
- 根据①所得,我们可以使用二叉树的广度优先遍历(BFS)来进行层级的处理。
- 最底层最左边的节点就是最后一层的第一个节点
- 可以使用一个
bottomLeft来保存每层最左边的节点的值。没当新的层级出现时候,将bottomLeft的值变更为第一个节点的值。 - 需要区分不同的层,我们采用两个队列的方式来实现
代码实现
function findBottomLeftValue(root){
let q1 = new Queue();
let q2 = new Queue();
q1.enqueue(root);
let bottomLeft = root.val;
while(!q1.isEmpty()){
let node = q1.dequeue();
if(node.left !=null){
q2.enqueue(node.left)
}
if(node.right !=null){
q2.enqueue(node.right)
}
if(q1.isEmpty()){
q1 = q2;
q2 = new Queue();
// 当q1为空时,开始遍历下一层,如果下一层还有节点,则更新bottomLeft
if(!q1.isEmpty()){
bottomLeft = q1.peek().val;
}
}
}
return bottomLeft
}
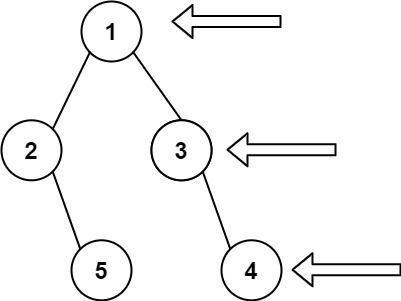
二叉树的右侧视图
题目描述:
❝输入一课二叉树,站在该二叉树的右侧,从上到下看到的节点构成二叉树的右侧视图。
❞
示例:输入: root = [1,2,3,null,5,null,4] 输出: [1,3,4]
分析
- 题目越怪,越需要向已知套路靠
- 根据右侧视图的概念和示例的结果分析,其实它就是想要 「每层最右边」的一个节点,因此二叉树的右侧视图其实就是从上到下每层最右边的节点
- 有几个关键节点
- 二叉树
- 区分不同的层
- 最右边的节点
- 直接二叉树bfs安排上
代码实现
function rightSideView(root){
let result = [];
if(root==null) return result;
let q1 = new Queue();
let q2 = new Queue();
q1.enqueue(root);
while(!q1.isEmpty()){
let node = q1.dequeue();
if(node.left!=null){
q2.enqueue(node.left)
}
if(node.right !=null){
q2.enqueue(node.right)
}
if(q1.isEmpty()){
result.push(node.val); //此时node是当前层的最后一个节点
q1= q2;
q2 = new Queue();
}
}
return result;
}
后记
「分享是一种态度」。
参考资料:剑指offer/leetcode官网/学习JavaScript数据结构与算法第3版
「全文完,既然看到这里了,如果觉得不错,随手点个赞和“在看”吧。」
本文由 mdnice 多平台发布