小白之CNN卷积神经网络详解
前言
本人是小白一枚,目前还在学习当中,文章内容仅供大家参考(部分内容和图片摘自其他文章,侵删!),若有问题欢迎大家指出!
一、基础知识
1.感知机
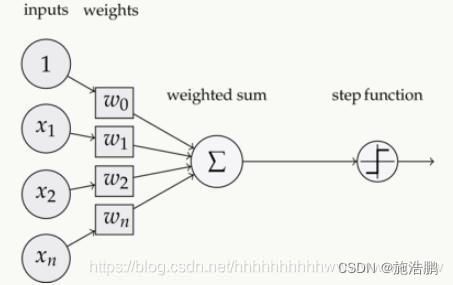
感知机是1957年,由Rosenblatt提出,是神经网络和支持向量机的基础。
上图是感知机的基本模型,可以看到,整个过程就是把输入内容与对应权重相乘再相加,最后用激活函数得出最后结果。图中,{x1...xn}为输入内容,{w1...wn}为对应权重,w0可以理解为偏置。
2.多层感知机 (MLP)
多层感知机(MLP,Multilayer Perceptron)也叫人工神经网络(ANN,Artificial Neural Network),有感知机推广而来,除了输入输出层,它中间可以有多个隐层,层与层之间是全连接的。计算方式和感知机相同。
3.前向传播(FP)和反向传播介绍(BP)
前向传播作用于每一层的输入,根据输入的内容逐层传播(计算)得出最后的结果。
反向传播作用于网络的输出,计算梯度由深到浅的更新网络参数。
关于这块内容,我看到一篇特别好的文章,想深入了解的可以看一下这篇文章,以后有机会我再总结。“反向传播算法”过程及公式推导(超直观好懂的Backpropagation)
4.激活函数
关于激活函数,我看了很多文章,但是一直搞不懂如何根据场景选择激活函数,这里推荐一篇文章,相信你看完这篇文章一定能有所收。常用的激活函数
选择激活函数常用的方法:先尝试使用ReLU函数,如果效果不佳尝试使用其变体,如:Leaky ReLU。尝试 tanh正切函数(以零为中心,零点处梯度为1)
如果是二分类使用sigmoid函数,多分类使用softmax函数。其中缘由你可以在我推荐的这篇文章找到答案。
5.其他
优化方法、损失函数等等在这里不一一介绍了,网上有很多对其介绍的优质文章。
二、CNN卷积神经网络
终于到了本文章的重点介绍内容,相信很多人都对CNN卷积神经网络不陌生,起码知道它的存在,那现在我们共同探讨一下CNN到底是什么?
在这里先给出CNN卷积神经网络百度上面的定义:
卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks),是深度学习(deep learning)的代表算法之一,擅长处理图像特别是图像识别等相关机器学习问题。
1.卷积层
1.1 什么是卷积?
卷积是一个结果,并非过程。我们通常学习的是卷积操作的过程(卷积运算)。它是一种有效提取图片特征的方法 。 一般用一个正方形卷积核,遍历图片上的每一个像素点。图片与卷积核重合区域内相对应的每一个像素值,乘卷积核内相对应点的权重,然后求和, 再加上偏置后,最后得到输出图片中的一个像素值。
1.2 常见的卷积核
输出图片亮度:卷积核总和为0(变为黑色)或者1(亮度不变)
锐化卷积核:强调物体边缘,图片整体。常见的锐化卷积核(三乘三为例:周围全是-1,中间值越小图像更清晰锐利)
边缘检测卷积核:边缘检测的作用为突出某个方向的特征。(卷积核特点:正数那边是想突出的那一部分)
浮雕卷积核:给图像一种3D阴影的效果。(卷积核特点:右斜对角线为零,左上为负,右下为正)
1.3 卷积神经网络的进化史
AlexNet-->VGGNet-->GoogleNet-->ResNet
Xception-->ShuffleNet-->SENet
详细了解可以去看相应文章。
1.4 卷积操作的三种情况
图片分为灰色图和彩色图,卷积核也可以有多个,下面介绍卷积操作的三种情况。
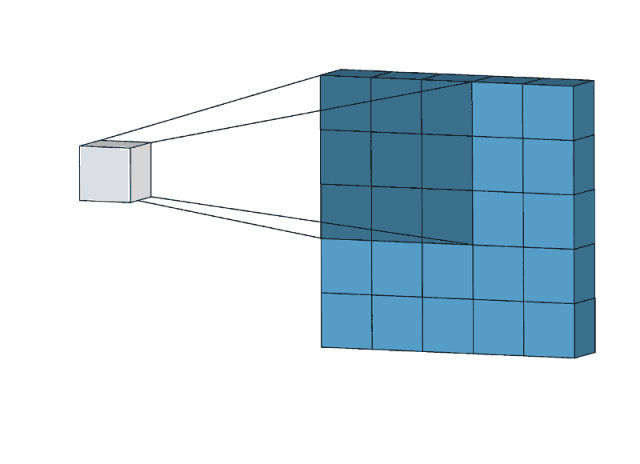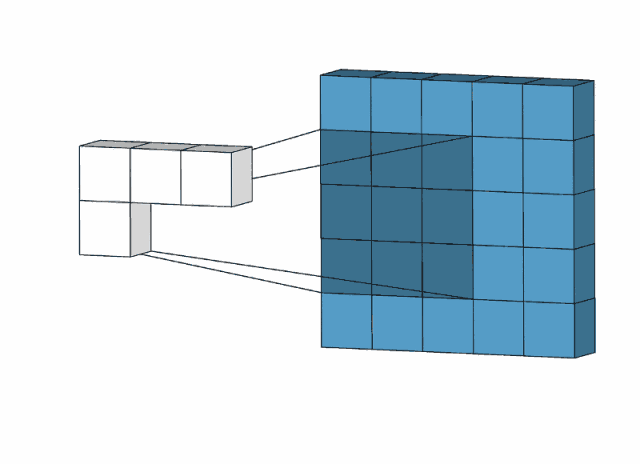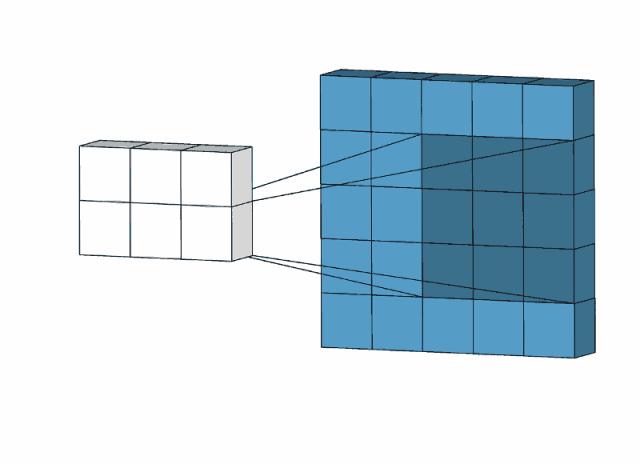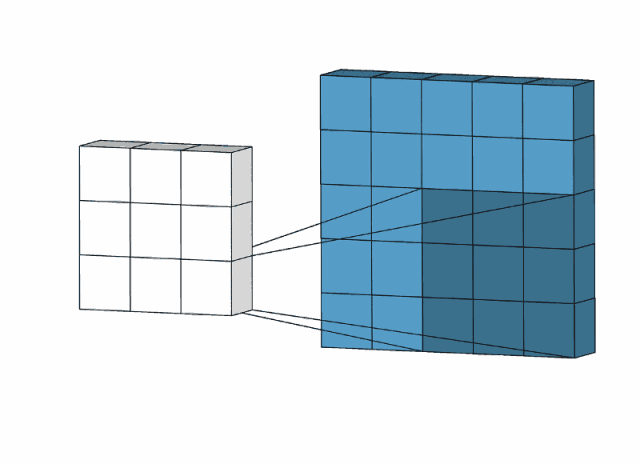
1.4.1 单通道+单卷积核
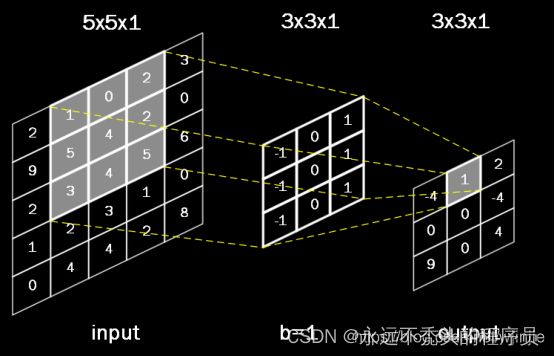
这里的单通道指的是灰度图,单卷积核指的是一个卷积核
上图的输入是5×5×1的灰度图,1代表通道数,5×5是分辨率(图片大小),里面的值为灰度值。所用的卷积核为3×3的卷积核(本文提到的边缘检测卷积核,正数在右边,突出右边,总和为0,输出为灰度图)
1.4.2 多通道+单卷积核
这里以RGB彩色图为例,输入的图片包含了红、绿、蓝三层数据,卷积核的深度(通道数)应该等于输入图片的通道数,所以使用 3x3x3的卷积核。
![]()
注:这里还是单个卷积核的情况,但是一个卷积核可以有多个通道。默认情况下,卷积核的通道数等于输入图片的通道数。
1.4.3 多通道+多卷积核
这种形式在卷积神经网络中最常见,这里最重要的就是区分卷积核的通道数和个数,总的来说就是卷积核的通道数等于输入图片的通道数,卷积核的个数等于输出的通道数。计算过程是多次多通道+单卷积核的计算(多次=卷积核的个数,每计算一次输出一个通道)
![]()
例如:上图中,输入[1,h,w,3]代表1张3通道分辨率为h×w的图片,卷积核[k,k,3,2]代表2个3通道大小为3×3的卷积核(因为输入图片为3通道,所以卷积核通道必须为3)。因为卷积核个数为2,所以输出的结果也为两个通道(每个通道都是一次多通道+单卷积核的输出)。
1.5 padding填充和stride步长
stride步长:卷积核每次滑动的距离。
padding填充:经过卷积操作之后的图片大小与输入的图片大小不一致,所以要进行填充操作,一般都是填充0。
(1)全零填充padding='same’
使用same时,会自动对原图进行全0填充,当步长为1时,可以保证输出的图片与输入的图片尺寸一致。输出尺寸计算公式:输入长/步长 (向上取整)
(2)不填充padding='valid’
使用valid时,不进行任何填充,直接进行卷积。输出尺寸计算公式:(输入长-核长)/步长+1 (向下取整)
(3)自定义填充
一般分为上下左右四个方向,可以根据自己需要进行填充。
2.池化层
随着网络层数的增加,所需要训练的参数也随之增加,这样不但计算量增加而且容易造成过拟合问题。CNN卷积神经网络使用池化操作解决上述问题,为了有效地减少计算量,池化就是将输入图像进行缩小,减少像素信息,只保留重要信息;为了有效地解决过拟合问题,池化可以减少数据,但特征的统计属性仍能够描述图像,而由于降低了数据维度,可以有效地避免过拟合。
池化主要有两种,除了 最大值池化(Max Pooling) 之外,还有 平均值池化(Average pooling)
(1)最大池化(Max Pooling),从局部相关元素集中选取最大的一个元素值。意义:最大池化可以获取局部信息,可以更好保留纹理上的特征。如果不用观察物体在图片中的具体位置,只关心其是否出现,则使用最大池化效果比较好。
卷积+最大池化约等于平移不变性,比如对图像分类任务来说,图像中的目标不管被移动到图片的哪个位置,得到的结果(标签)应该是相同的,这就是卷积神经网络中的平移不变性。
(2)平均池化(Average Pooling),从局部相关元素集中计算平均值并返回。意义:平均池化往往能保留整体数据的特征,能凸出背景的信息。
3.全连接层
这里的全连接层就是一个普通的多层神经网络。
输入图片经过多次的卷积和池化操作,获得原始图片的特征图,再将特征图打平送入全连接层,最后输出预测结果。
4.CNN卷积神经网络训练流程
训练基本流程:
Step 1:用随机数初始化所有的卷积核和参数/权重(如果手里训练数据不多,可以考虑使用预训练+微调的方式进行训练,优势:收敛快+准确率高)
Step 2:将训练图片作为输入,执行前向步骤(卷积, ReLU,池化以及全连接层的前向传播)并计算每个类别的对应输出概率。
Step 3:计算输出层的总误差
Step 4:反向传播算法计算误差相对于所有权重的梯度,并用梯度下降法更新所有的卷积核和参数/权重的值,以使输出误差最小化
注:卷积核个数、卷积核尺寸、网络架构这些参数,是在 Step 1 之前就已经固定的,且不会在训练过程中改变——只有卷积核矩阵和神经元权重会更新。
和多层神经网络一样,卷积神经网络中的参数训练也是使用误差反向传播算法。
关于卷积层和池化层的训练,需要提一下,是将卷积层和池化层都改为多层神经网络的形式。
![]()
![]()
5.总结
CNN两大核心:局部连接和权值共享
1.局部连接:
- 一般认为图像的空间联系是局部的像素联系比较密切,而距离较远的像素相关性较弱,因此,每个神经元没必要对全局图像进行感知,只要对局部进行感知,然后在更高层将局部的信息综合起来得到全局信息。
- 即网络部分连通(这里指的是将卷积层和池化层变成神经网络的形式,上面提到过),每个神经元只与上一层的部分神经元相连,只感知局部,而不是整幅图像。(滑窗实现)
2.参数共享:
-
在局部连接中,每个神经元的参数都是一样的,即:同一个卷积核在图像中都是共享的。(理解:卷积操作实际是在提取一个个局部信息,而局部信息的一些统计特性和其他部分是一样的,也就意味着这部分学到的特征也可以用到另一部分上。所以对图像上的所有位置,都能使用同样的学习特征。)卷积核共享有个问题:提取特征不充分,可以通过增加多个卷积核来弥补,可以学习多种特征。
想学习CNN代码请移步到我个人的Gitee:(难点都标有注释,适合小白,是本人学习时标注的)CNN.py · superwarrior007/python练习 - 码云 - 开源中国 (gitee.com)
主要参考文章:https://blog.csdn.net/qq_36816848/article/details/122286610?spm=1001.2014.3001.5506