剑指Offer C++ --- 数组篇3
1.连续子数组的最大和
涉及到:有重叠子问题和最优子结构,那么首先想到的就是动态规划
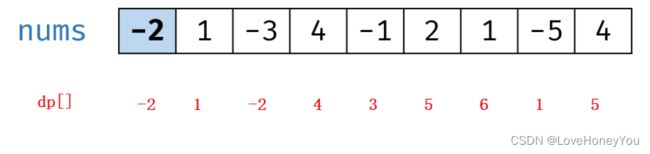
状态定义: dp[i]表示以nums[i]结尾的子数组的最大和
状态方程: dp[i]的初值为nums[i]
如果:dp[i] > 0 ==》 dp[i] = nums[i]+dp[i-1]
否则:dp[i] <= 0 ==》 什么也不做
max 表示最大子数组的和,如果当前子数组的和 > max 则更新max
int maxSubArray(vector& nums)
{
int pre = 0;
int cur = 0;
int max = nums[0];
for(auto x : nums)
{
cur = x;
if(pre > 0)
{
cur += pre;
}
if(cur > max)
{
max = cur;
}
pre = cur;
}
return max;
} 2.统计一个数字在排序数组中出现的次数
思路:二分法+线性探测
int search(vector& nums, int target)
{
int i = 0;
int j = nums.size()-1;
int mid = 0;
int count = 1;
while(i<=j)
{
mid = i+((j-i)>>1);
if(nums[mid] == target)
{
break;
}
else if(nums[mid] < target)
{
i = mid+1;
}
else
{
j = mid-1;
}
}
//没找到
if(i > j)
{
return 0;
}
//找到了
i = mid-1;
j = mid+1;
//向右探测
while(j <= nums.size()-1)
{
if(nums[mid] == nums[j])
{
++count;
++j;
}
else
{
break;
}
}
//向左探测
while(i >= 0)
{
if(nums[mid] == nums[i])
{
++count;
--i;
}
else
{
break;
}
}
return count;
} 3. 0~n-1中缺失的数字
int missingNumber(vector& nums)
{
int i = 0;
for(auto x : nums)
{
if(i++ != x)
{
return x-1;
}
}
return -1;
} 4. 和为s的两个数字
vector twoSum(vector& nums, int target)
{
int min = 0;
int max = nums.size()-1;
vector vec;
while(min < max)
{
if(nums[min] + nums[max] < target)
{
++min;
}
else if(nums[min] + nums[max] > target)
{
--max;
}
else
{
vec.push_back(nums[min]);
vec.push_back(nums[max]);
break;
}
}
return vec;
} 5.扑克牌中的顺子
思路:除0外,最大牌-最小牌 < 5
除0外,牌不能有重复
bool isStraight(vector& nums)
{
set s;
int min = 14;
int max = 0;
//五张牌除0外,其余数字不能重复,最大的牌号 - 最小的 < 5 就证明可以组成顺子
for(auto x : nums)
{
if(x == 0)
{
continue;
}
max = std::max(max,x); //最大牌
min = std::min(min,x); //最小牌
if(s.find(x) != s.end())
{
//重复牌
return false;
}
s.insert(x);
}
return max - min < 5;
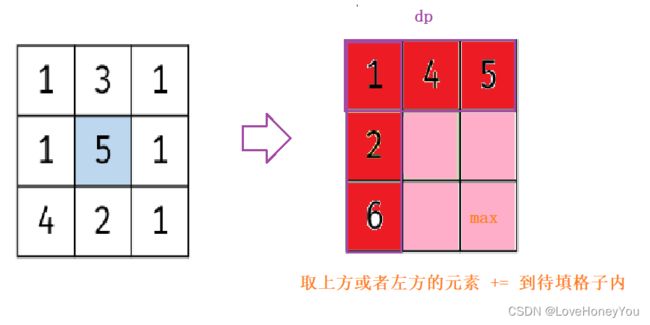
} 6.礼物的最大价值
int maxValue(vector>& grid)
{
int m = grid.size(); //行数
int n = grid[0].size(); //列数
//初始化第一行
//行不动,列动
for(int i = 1; i 7.数组中数字出现的次数
思路:位运算,异或
vector singleNumbers(vector& nums)
{
//0异或任何数等于其本身
//相同的数异或等于0
//异或有交换律
int z = 0;
for(auto x : nums)
{
z ^= x;
}
int m = 1;
//找到最低位的1
while((m&z) == 0)
{
m <<= 1;
}
int i = 0;
int j = 0;
//根据m划分为两组
//每组只有一个数会出现一次
for(auto x : nums)
{
if((m&x) == 0)
{
i ^= x;
}
else
{
j ^= x;
}
}
return vector{i,j};
} 8.数组中数字出现的次数 II
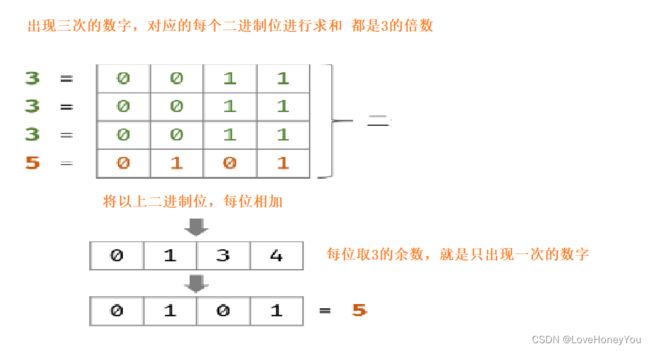
思路:
将容器中所有元素对应的二进制位存起来,对每个元素进行 &1后,>>1 存储下一位
在存储二进制位的容器,是由低位到高位
找只出现一次的数字时,对存储的每一位进行%3,然后 |= 先从高位开始
int singleNumber(vector& nums)
{
vector sumBin(32,0);
for(auto x : nums)
{
for(int i = 0; i<32; ++i)
{
//由低位到高位
sumBin[i] += (x&1);
x >>= 1;
}
}
int res = 0;
int m = 3;
for(int i = 0; i<32; ++i)
{
res <<= 1;
//从高位到低位
res |= (sumBin[31-i]%3);
}
return res;
} 9.股票的最大利润
思路:以最低价买入,以最高价卖出
dp[i] = dp[i-1] + prices - min(prices[0 -》i-1]);
int maxProfit(vector& prices)
{
int dp = 0; //最大利润
int minvalue = INT_MAX;
for(auto x:prices)
{
//寻找最低价买入
if(minvalue > x)
{
minvalue = x;
continue;
}
//高价售出
dp = max(dp,prices-minvalue);
}
return dp;
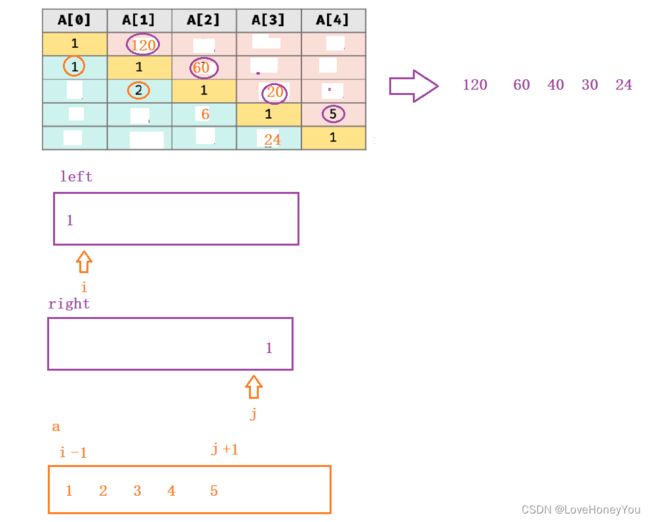
} 10.构建乘积数组
vector constructArr(vector& a)
{
if(a.empty())
{
return {};
}
vector left(a.size(),0);
vector right(a.size(),0);
vector b(a.size(),0);
int length = a.size();
left[0] = 1;
right[length-1] = 1;
for(int i = 1; i < length; ++i)
{
left[i] = left[i-1]*a[i-1];
}
for(int j = length-2; j>=0; --j)
{
right[j] = right[j+1]*a[j+1];
}
for(int k = 0; k