【车间调度】基于matlab NSGA2算法求解车间调度优化问题【含Matlab源码 2418期】

⛄一、车间调度简介

1 作业车间调度问题描述
作业车间调度问题（Job Shop Scheduling, JSP）是最经典的几个NP-hard问题之一。其应用领域极其广泛，涉及航母调度，机场飞机调度，港口码头货船调度，汽车加工流水线等。
JSP问题描述：一个加工系统有M台机器，要求加工N个作业，其中，作业i包含工序数为Li。令，则L为任务集的总工序数。其中，各工序的加工时间已确定，并且每个作业必须按照工序的先后顺序加工。调度的任务是安排所有作业的加工调度排序，约束条件被满足的同时，使性能指标得到优化。
作业车间调度需要考虑如下约束:
Cons1：每道工序在指定的机器上加工，且必须在其前一道工序加工完成后才能开始加工；
Cons2：某一时刻1台机器只能加工1个作业；
Cons3：每个作业只能在1台机器上加工1次；
Cons4：各作业的工序顺序和加工时间已知，不随加工排序的改变而改变。
2 问题实例
下面给出作业车间调度问题的一个实例，其中每个工序上标注有一对数值（m,p），其中，m表示当前工序必须在第m台机器上进行加工，p表示第m台机器加工当前工序所需要的加工时间。（注：机器和作业的编号从0开始）
jop0=[(0,3),(1,2),(2,2)]
jop1=[(0,2),(2,1),(1,4)]
jop2=[(1,4),(2,3)]
在这个例子中，作业jop0有3道工序：它的第1道工序上标注有(0,3)，其表示第1道工序必须在第0台机器上进行加工，且需要3个单位的加工时间；它的第2道工序上标注有(1,2)，其表示第2道工序必须在第1台机器上进行加工，且需要2个单位的加工时间；余下的同理。总的来说，这个实例中共有8道工序。
该问题的一个可行解是L=8道工序开始时间的一个排列，且满足问题的约束。下图给出了一个可行解（注：该解不是最优解）的示例：

⛄二、nsgaII算法简介

NSGA：非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm)

种群分层：
Tips:此处存在重复对比情况，即X1 与 X2 进行了两次对比
虚拟适应度：目标函数值
共享小生境技术：

同一小生境内的种群，适应度互相减小。相似度高的、小生境内个体多的种群适应度减少程度更大。
通过这样的方式可以保证非支配层的每个个体拥有不同的适应度值。（这个没有懂）
NSGA-II：带精英策略的非支配排序遗传算法
快速非支配排序算法：

伪代码：


如图，D点被A和C点支配，所以D点的np为2，A点支配D和E，所以A点的Sp={D，E}。
该排序算法分级与NSGA中的结果不一样
拥挤度和拥挤度比较算子
密度估计：根据每一目标函数计算该点两侧的两个点的平均距离，该值作为以最近邻居作为顶点的长方体周长的估计（作为拥挤系数）。如下图，第i个解的拥挤系数为他周围长方体的长度（虚线表示）。
计算拥挤系数需要对每一目标函数进行排序。
每个非支配层的边界的个体拥挤度为无穷。

拥挤度有多种计算方式
1.直接计算长方体边长

2.需要除以…

拥挤度比较算子：

主程序：

精英策略：


NSGA-II 程序流程图

需要输入的变量是：规模N、迭代次数

⛄三、部分源代码

%% 对初始种群开始排序 快速非支配排序
% 使用非支配排序对种群进行排序。该函数返回每个个体对应的排序值和拥挤距离，是一个两列的矩阵。
% 并将排序值和拥挤距离添加到染色体矩阵中
%x：决策矩阵 M：优化目标数量 V：决策变量个数
function [p_matrix,m_matrix] = non_domination_sort_mod(pro_matrix,mac_matrix)
[N, ~] = size(pro_matrix);% N为矩阵x的行数，也是种群的数量
M=5;%优化目标数量
V=size(pro_matrix,2)-M;%决策变量个数
front = 1;
F(front).f = [];%记录paret o解集等级为front级的个体集合
individual = [];%用于存放被某个个体支配的个体集合

for i = 1 : N
    individual(i).n = 0;%n是个体i被支配的个体数量
    individual(i).p = [];%p是被个体i支配的个体集合
    for j = 1 : N
        dom_less = 0;
        dom_equal = 0;
        dom_more = 0;
        for k = 1 : M        %判断个体i和个体j的支配关系
            if (pro_matrix(i,V + k) < pro_matrix(j,V + k))  
                dom_less = dom_less + 1;
            elseif (pro_matrix(i,V + k) == pro_matrix(j,V + k))
                dom_equal = dom_equal + 1;
            else
                dom_more = dom_more + 1;
            end
        end
        if dom_less == 0 && dom_equal ~= M % 说明i受j支配，相应的n加1
            individual(i).n = individual(i).n + 1;
        elseif dom_more == 0 && dom_equal ~= M % 说明i支配j,把j加入i的支配合集中
            individual(i).p = [individual(i).p j];
        end
    end   
    if individual(i).n == 0 %个体i非支配等级排序最高，属于当前最优解集，相应的染色体中携带代表排序数的信息
        pro_matrix(i,M + V + 1) = 1;
        F(front).f = [F(front).f i];%等级为1的非支配解集
    end
end

%上面的代码是为了找出等级最高的非支配解集
%下面的代码是为了给其他个体进行分级
while ~isempty(F(front).f)
Q = []; %存放下一个front集合
for i = 1 : length(F(front).f)%循环当前支配解集中的个体
if ~isempty(individual(F(front).f(i)).p)%个体i有自己所支配的解集
for j = 1 : length(individual(F(front).f(i)).p)%循环个体i所支配解集中的个体
individual(individual(F(front).f(i)).p(j)).n = …%…表示的是与下一行代码是相连的，这里表示个体j的被支配个数减1
individual(individual(F(front).f(i)).p(j)).n - 1;
if individual(individual(F(front).f(i)).p(j)).n == 0% 如果q是非支配解集，则放入集合Q中
pro_matrix(individual(F(front).f(i)).p(j),M + V + 1) = …%个体染色体中加入分级信息
front + 1;
Q = [Q individual(F(front).f(i)).p(j)];
end
end
end
end
front = front + 1;
F(front).f = Q;
end

[~,index_of_fronts] = sort(pro_matrix(:,M + V + 1));%对个体的代表排序等级的列向量进行升序排序 temp为排序完成的列 index_of_fronts表示排序后的值对应原来的索引
for i = 1 : length(index_of_fronts)
    sorted_based_on_front(i,:) = pro_matrix(index_of_fronts(i),:);%sorted_based_on_front中存放的是x矩阵按照排序等级升序排序后的矩阵
    m_matrix(i,:)=mac_matrix(index_of_fronts(i),:);
end
current_index = 0;

%% Crowding distance 计算每个个体的拥挤度

for front = 1:(length(F) - 1)%这里减1是因为代码55行这里，F的最后一个元素为空，这样才能跳出循环。所以一共有length-1个排序等级
    distance = 0;
    y = [];
    previous_index = current_index + 1;
    for i = 1 : length(F(front).f)
        y(i,:) = sorted_based_on_front(current_index + i,:);%y中存放的是排序等级为front的集合矩阵

% z(i,:) = mac_sorted_based(current_index+i,:);%z中存放是等级为front的对应的加工设备集合矩阵
end
current_index = current_index + i;%current_index =i
sorted_based_on_objective = [];%存放基于拥挤距离排序的矩阵
for i = 1 : M
[~, index_of_objectives] = …
sort(y(:,V + i));%按照目标函数值排序
sorted_based_on_objective = [];
for j = 1 : length(index_of_objectives)
sorted_based_on_objective(j,:) = y(index_of_objectives(j);% sorted_based_on_objective存放按照目标函数值排序后的x矩阵
% mac_sorted_matrix(j,:)=z(index_of_objectives(j)
end
f_max = …
sorted_based_on_objective(length(index_of_objectives), V + i);%fmax为目标函数最大值 fmin为目标函数最小值
f_min = sorted_based_on_objective(1, V + i);
y(index_of_objectives(length(index_of_objectives)),M + V + 1 + i)…%对排序后的第一个个体和最后一个个体的距离设为无穷大
= inf;
y(index_of_objectives(1),M + V + 1 + i) = inf;
for j = 2 : length(index_of_objectives) - 1%循环集合中除了第一个和最后一个的个体
next_obj = sorted_based_on_objective(j + 1,V + i);
previous_obj = sorted_based_on_objective(j - 1,V + i);
if (f_max - f_min == 0)
y(index_of_objectives(j),M + V + 1 + i) = inf;
else
y(index_of_objectives(j),M + V + 1 + i) = …
(next_obj - previous_obj)/(f_max - f_min);
end
end
end
distance = [];
distance(:,1) = zeros(length(F(front).f),1);
for i = 1 : M
distance(:,1) = distance(:,1) + y(:,M + V + 1 + i);
end
y(:,M + V + 2) = distance;
y = y(:,1 : M + V + 2);
p_matrix(previous_index:current_index,:) = y;
end
end

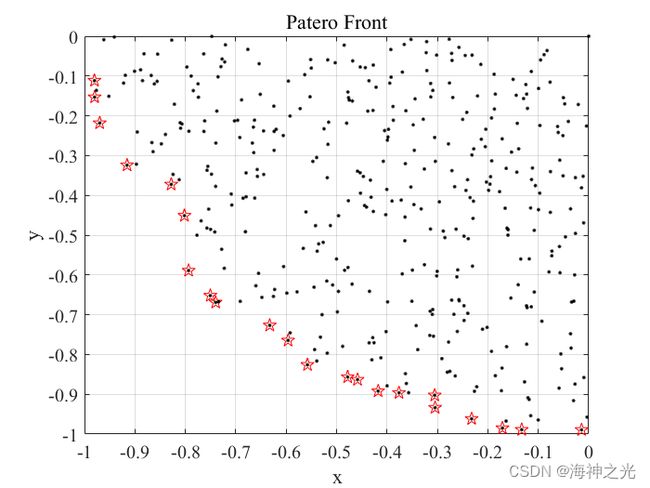
⛄四、运行结果

⛄五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除