快速导向滤波 matlab,导向滤波小结:从导向滤波(guided filter)到快速导向滤波(fast guide filter)的原理,应用及opencv实现代码...
http://blog.csdn.net/kuweicai/article/details/78385871
1. 导向滤波简介
导向滤波是何凯明在学生时代提出的一个保边滤波(edge-preserving smoothing)算法。何凯明在cv圈应该算是名人了,学生时代关于图像去雾的研究就以第一作者的身份获得Best Paper Award(CVPR 2009),而且今年刚刚又斩获Marr Prize(ICCV 2017)。更多关于何凯明的最新研究动态可以点击以下链接何凯明。
导向滤波顾名思义,就是有选择(导向)性的滤波,其与我们经常提及的高斯滤波、双边滤波相比,它具有导向性,说具体点就是,它通过输入一副图像(矩阵)作为导向图,这样滤波器就知道什么地方是边缘,这样就可以更好的保护边缘,最终达到在滤波的同时,保持边缘细节。所以有个说法是导向滤波是各向异性的滤波器,而高斯滤波、双边滤波这些是各向同性滤波器,我觉得也是很贴切。
导向滤波作为一种保边滤波,可以运用在很多场合,比如美颜,去雾,三维重建等。
如果你仅仅只是需要运用这个算法,现在opencv 3.0和MATLAB 14都已经添加了guided filter的API,可以直接调用。
opencv中的API如下void cv::ximgproc::guidedFilter(),具体的可以参考opencv的帮助文档关于导向滤波的介绍guidedFilter。
但是需要提醒的是,opencv中guidedFilter()函数包含在ximgproc模块下,但是从官方下载的标准的opencv.exe程序中并不包含该模块,需要分别下载opencv的source文件和contrib模块的source文件,然后自己编译,具体可以参考opencv3.1.0+contrib模块编译总结。
2. 导向滤波的原理
查看了很多相关的资料,觉得白马负金羁的导向滤波(Guided Filter)的解析与实现一文将其原理解释的非常通俗易懂了,这里就不再赘述。仅给出最后的推导结果,其中fmean为一个窗口半径为r的均值滤波器(对应的窗口大小为2r+1),corr为相关,var为方差,cov为协方差。
3. opencv实现代码
这一部分主要参考了
OpenCV导向滤波(引导滤波)实现(Guided Filter)代码,以及使用颜色先验算法去雾中的代码,进行了修改和注释。GuidedFilter()调用opencv自带的boxFilter()函数来实现求取平均值。关于opencv自带的boxFilter()函数的相关介绍可以参考
boxFilter。
GuidedFilter()的代码,比较容易理解:
cv::Mat GuidedFilter(cv::Mat I,cv::Mat p,intr,doubleeps)
{
/*
% GUIDEDFILTER O(N) time implementation of guided filter.
%
% - guidance image: I (should be a gray-scale/single channel image)
% - filtering input image: p (should be a gray-scale/single channel image)
% - local window radius: r
% - regularization parameter: eps
*/
cv::Mat _I;
I.convertTo(_I, CV_64FC1,1.0/255);
I = _I;
cv::Mat _p;
p.convertTo(_p, CV_64FC1,1.0/255);
p = _p;
//[hei, wid] = size(I);
inthei = I.rows;
intwid = I.cols;
r=2*r+1;//因为opencv自带的boxFilter()中的Size,比如9x9,我们说半径为4
//mean_I = boxfilter(I, r) ./ N;
cv::Mat mean_I;
cv::boxFilter(I, mean_I, CV_64FC1,cv::Size(r, r));
//mean_p = boxfilter(p, r) ./ N;
cv::Mat mean_p;
cv::boxFilter(p, mean_p, CV_64FC1,cv::Size(r, r));
//mean_Ip = boxfilter(I.*p, r) ./ N;
cv::Mat mean_Ip;
cv::boxFilter(I.mul(p), mean_Ip, CV_64FC1,cv::Size(r, r));
//cov_Ip = mean_Ip - mean_I .* mean_p; % this is the covariance of (I, p) in each local patch.
cv::Mat cov_Ip = mean_Ip - mean_I.mul(mean_p);
//mean_II = boxfilter(I.*I, r) ./ N;
cv::Mat mean_II;
cv::boxFilter(I.mul(I), mean_II, CV_64FC1,cv::Size(r, r));
//var_I = mean_II - mean_I .* mean_I;
cv::Mat var_I = mean_II - mean_I.mul(mean_I);
//a = cov_Ip ./ (var_I + eps); % Eqn. (5) in the paper;
cv::Mat a = cov_Ip / (var_I + eps);
//b = mean_p - a .* mean_I; % Eqn. (6) in the paper;
cv::Mat b = mean_p - a.mul(mean_I);
//mean_a = boxfilter(a, r) ./ N;
cv::Mat mean_a;
cv::boxFilter(a, mean_a, CV_64FC1,cv::Size(r, r));
//mean_b = boxfilter(b, r) ./ N;
cv::Mat mean_b;
cv::boxFilter(b, mean_b, CV_64FC1,cv::Size(r, r));
//q = mean_a .* I + mean_b; % Eqn. (8) in the paper;
cv::Mat q = mean_a.mul(I) + mean_b;
returnq;
}
需要注意的是,上面的函数只能对单一通道进行处理(如果是多通道,需要split后进行滤波,然后merge)。下面是调用GuidedFilter(),r=16, eps=0.01,对原图像进行滤波的结果。
4. 快速导向滤波
导向滤波的时间复杂度为O(N),其中N为像素点的个数。
何凯明在2015又发表了一篇《Fast Guided Filter》的文章,阐述了一种很实用的更快速的导向滤波流程。如下所示。其本质是通过下采样减少像素点,计算mean_a & mean_b后进行上采样回复到原有的尺寸大小。假设缩放比例为s,那么缩小后像素点的个数为N/s^2,那么时间复杂度变为O(N/s^2)(只是需要注意的是上采样和下采样本身也是有时间消化的)。
基于上面的理论,只需调用resize()函数来实现下采样和上采样,关于resize()函数的使用可以参考
resize()代码如下:
cv::Mat fastGuidedFilter(cv::Mat I_org,cv::Mat p_org,intr,doubleeps,ints)
{
/*
% GUIDEDFILTER O(N) time implementation of guided filter.
%
% - guidance image: I (should be a gray-scale/single channel image)
% - filtering input image: p (should be a gray-scale/single channel image)
% - local window radius: r
% - regularization parameter: eps
*/
cv::Mat I,_I;
I_org.convertTo(_I, CV_64FC1,1.0/255);
resize(_I,I,Size(),1.0/s,1.0/s,1);
cv::Mat p,_p;
p_org.convertTo(_p, CV_64FC1,1.0/255);
//p = _p;
resize(_p, p, Size(),1.0/s,1.0/s,1);
//[hei, wid] = size(I);
inthei = I.rows;
intwid = I.cols;
r = (22* r +1)/s+1;//因为opencv自带的boxFilter()中的Size,比如9x9,我们说半径为4
//mean_I = boxfilter(I, r) ./ N;
cv::Mat mean_I;
cv::boxFilter(I, mean_I, CV_64FC1,cv::Size(r, r));
//mean_p = boxfilter(p, r) ./ N;
cv::Mat mean_p;
cv::boxFilter(p, mean_p, CV_64FC1,cv::Size(r, r));
//mean_Ip = boxfilter(I.*p, r) ./ N;
cv::Mat mean_Ip;
cv::boxFilter(I.mul(p), mean_Ip, CV_64FC1,cv::Size(r, r));
//cov_Ip = mean_Ip - mean_I .* mean_p; % this is the covariance of (I, p) in each local patch.
cv::Mat cov_Ip = mean_Ip - mean_I.mul(mean_p);
//mean_II = boxfilter(I.*I, r) ./ N;
cv::Mat mean_II;
cv::boxFilter(I.mul(I), mean_II, CV_64FC1,cv::Size(r, r));
//var_I = mean_II - mean_I .* mean_I;
cv::Mat var_I = mean_II - mean_I.mul(mean_I);
//a = cov_Ip ./ (var_I + eps); % Eqn. (5) in the paper;
cv::Mat a = cov_Ip / (var_I + eps);
//b = mean_p - a .* mean_I; % Eqn. (6) in the paper;
cv::Mat b = mean_p - a.mul(mean_I);
//mean_a = boxfilter(a, r) ./ N;
cv::Mat mean_a;
cv::boxFilter(a, mean_a, CV_64FC1,cv::Size(r, r));
Mat rmean_a;
resize(mean_a, rmean_a, Size(I_org.cols, I_org.rows),1);
//mean_b = boxfilter(b, r) ./ N;
cv::Mat mean_b;
cv::boxFilter(b, mean_b, CV_64FC1,cv::Size(r, r));
Mat rmean_b;
resize(mean_b, rmean_b, Size(I_org.cols, I_org.rows),1);
//q = mean_a .* I + mean_b; % Eqn. (8) in the paper;
cv::Mat q = rmean_a.mul(_I) + rmean_b;
returnq;
}
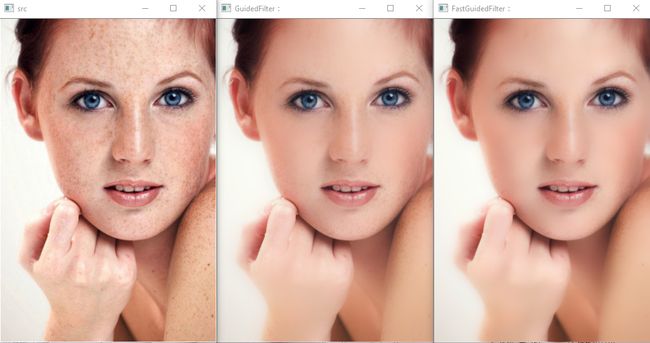
取s==8,计算结果和之前的guidedFilter()的计算结果如下所示:
而计算时间却从 338.808ms降到100.856ms,但是滤波结果从肉眼观察几乎没有降低。