时间序列最常用方法总结（附代码）

平时工作中每天都在和时间序列打交道，对时间序列分析进行研究是有必要的

分享和交流一些自己的在时序处理方面的心得，提供一些思路

介绍时序的发展情况，以及目前业界常用的方法

代码希望能模板化，能直接复制过去使用

时序方法发展

技术交流

技术要学会分享、交流，不建议闭门造车。一个人走的很快、一堆人可以走的更远。

本文来自技术群粉丝分享整理，文章源码、数据、技术交流，均可加交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、添加微信号：pythoner666，备注：来自CSDN +备注来意
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群

时间序列特征

series = trend + seasons + dependence+ error

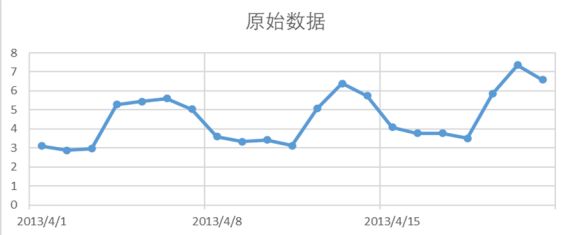
趋势

时间序列的趋势分量表示该序列均值的持续的、长期的变化

Df['ma20'] = Df['amt'].rolling(20).mean()

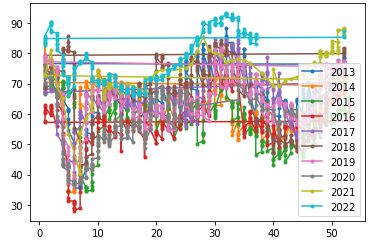
周期性（季节性）

季节时序图

def plot_season(Df):
    df = Df.copy()
    # 计算每周属于哪一年
    df['year'] = df['date'].dt.year
    # 计算每周为一年当中的第几周
    df['week_of_year'] = df['date'].dt.weekofyear
    for year in df['year'].unique():
        tmp_df = df[df['year'] == year]
        plt.plot(tmp_df['week_of_year'], tmp_df['amt'], '.-', label=str(year))
    plt.legend()
    plt.show()

周期判断

如果每隔h个单位，ACF值有一个局部高峰，则数据存在以h为单位的周期性

from  statsmodels.graphics.tsaplots import plot_acf
plot_acf(Df['amt'], lags=500).show()

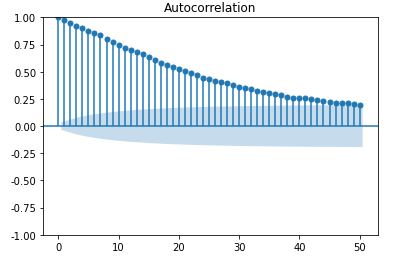
自相关性

自相关

自相关函数 autocorrelation function 有序的随机变量序列与其自身相比较 自相关函数反映了同一序列在不同时序的取值之间的相关性

from statsmodels.graphics.tsaplots import plot_acf
_ = plot_acf(Df['amt'], lags=50)

偏自相关

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(Df['amt'], lags=5)

残差

• 外部变量

• 残差

Prophet

官方文档：https://facebook.github.io/prophet/docs/quick_start.html#python-api

原理

模型结构

模型结构——关于时间的广义线性模型

• g(t):trend,用分段线性函数或逻辑增长曲线(logistic)拟合

• s(t):seasonality,用傅里叶级数拟合。可以叠加多个季节性，如weekly,yearly （s = s1+s2……）

• h(t):regressor，用线性函数拟合。可以叠加多个外部变量，如节假日、温度、活动（h = h1+h2+……）

• :模型残差 不用拟合

• 以上方程也可以写成乘法形式：

• 乘法形式和加法形式可以相互转换，乘法形式两边取对数就是加法形式

趋势

分段线性函数

线性趋势函数

分段线性趋势函数

• 超参数，由用户给出

• 分几段

• 参数，根据历史数据拟合

• k：曲线增长速率

• m：曲线的截距

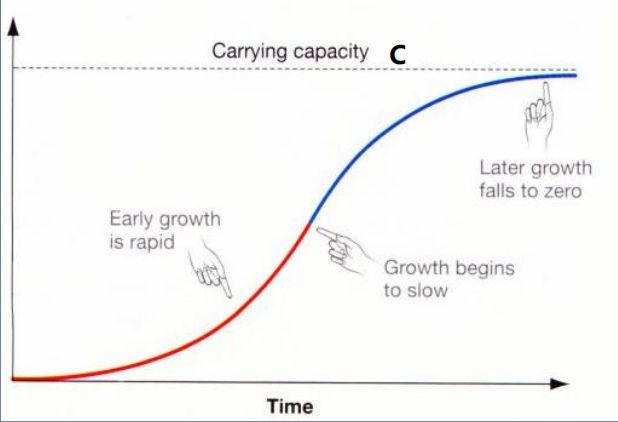
逻辑增长曲线

函数展示：https://www.desmos.com/calculator/8pnqou9ojy?lang=zh-CN

• 超参数

• C：渐近线

• 一共分几段

• 参数

• k：曲线增长速率

• m：拐点对应时间

周期性

任何周期性函数都可以表示成傅里叶级数

• 超参数：由用户给定

  傅里叶级数的阶数，越大，季节性曲线波动越大，越容易过拟合

• 参数：由历史数据拟合

  、系数

函数展示：(https://www.desmos.com/calculator/5prck2beq1?lang=zh-CN

外部因素

• : 模型输入， 外部因素在时刻的取值

  Z可以是0-1变量 （e.g.是否是法定假日，是否是春节，是否有促销）

  也可以是连续变量 （e.g.产品价格， 温度，降雨量)

• ：线性回归系数

算法流程

1️⃣ 先设定表达式（超参数）

2️⃣ 根据训练集数据求解参数

实践

发电耗煤预测

df_train = Df[ (Df['date']<'2022-01-01') & (Df['date']>='2018-01-01') ]
df_test =  Df[ (Df['date']>='2022-01-01')]

def FB(data):
    df = pd.DataFrame({
    'ds': data.date,
    'y': data.amt,
    })
#     df['cap'] = data.amt.values.max()
#     df['floor'] = data.amt.values.min()
    m = prophet.Prophet(
        changepoint_prior_scale=0.05, 
        daily_seasonality=False,
        yearly_seasonality=True, #年周期性
        weekly_seasonality=True, #周周期性
#         growth="logistic",
    )
    m.add_seasonality(name='monthly', period=30.5, fourier_order=5, prior_scale=0.1)#月周期性
    m.add_country_holidays(country_name='CN')#中国所有的节假日    
    m.fit(df)
    future = m.make_future_dataframe(periods=30, freq='D')#预测时长
#     future['cap'] = data.amt.values.max()
#     future['floor'] = data.amt.values.min()
    forecast = m.predict(future)
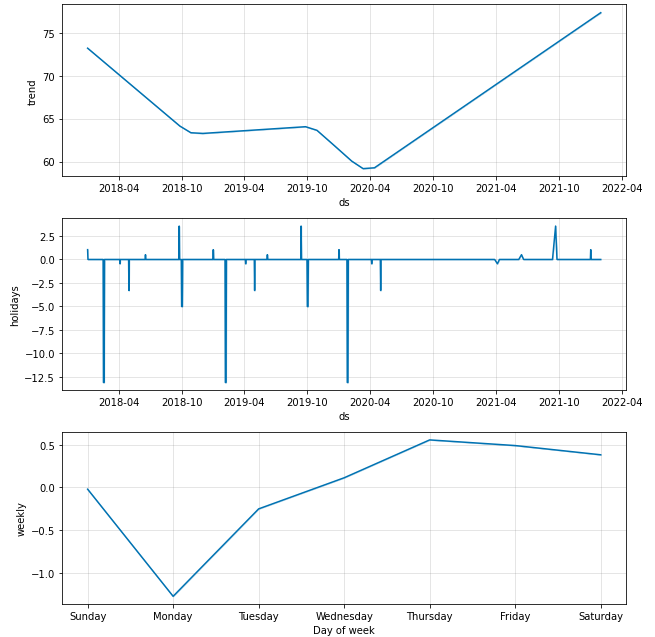
    fig = m.plot_components(forecast)
    fig1 = m.plot(forecast)
    a = add_changepoints_to_plot(fig1.gca(), m, forecast)
    return forecast,m

forecast,m = FB(df_train)

def FPPredict(data,m):
    df = pd.DataFrame({
    'ds': data.date,
    'y': data.amt,
    })
    df_predict = m.predict(df)
    df['yhat'] = df_predict['yhat'].values
    df = df.set_index('ds')
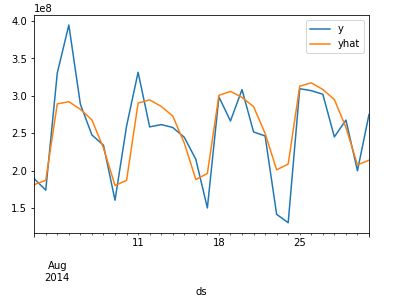
    df.plot()
    return df

df = FPPredict(df_test.tail(200),m)

申购赎回金额预测

kaggle notebook[1]

Purchase Redemption Data.zip

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import prophet
from prophet.diagnostics import cross_validation
from prophet.diagnostics import performance_metrics
from prophet.plot import plot_cross_validation_metric
import warnings
warnings.filterwarnings('ignore')

data_user = pd.read_csv('../input/purchase-redemption/Purchase Redemption Data/user_balance_table.csv')
data_user['report_date'] = pd.to_datetime(data_user['report_date'], format='%Y%m%d')
data_user.head()

data_user_byday = data_user.groupby(['report_date'])['total_purchase_amt','total_redeem_amt'].sum().sort_values(['report_date']).reset_index()
data_user_byday.head()

申购

#定义模型
def FB(data: pd.DataFrame):
    df = pd.DataFrame({
    'ds': data.report_date,
    'y': data.total_purchase_amt,
    })
#     df['cap'] = data.total_purchase_amt.values.max()
#     df['floor'] = data.total_purchase_amt.values.min()
    m = prophet.Prophet(
        changepoint_prior_scale=0.05, 
        daily_seasonality=False,
        yearly_seasonality=True, #年周期性
        weekly_seasonality=True, #周周期性
#         growth="logistic",
    )
#     m.add_seasonality(name='monthly', period=30.5, fourier_order=5, prior_scale=0.1)#月周期性
    m.add_country_holidays(country_name='CN')#中国所有的节假日    
    m.fit(df)
    future = m.make_future_dataframe(periods=30, freq='D')#预测时长
#     future['cap'] = data.total_purchase_amt.values.max()
#     future['floor'] = data.total_purchase_amt.values.min()
    forecast = m.predict(future)
    fig = m.plot_components(forecast)
    fig1 = m.plot(forecast)
    return forecast,m

result_purchase,purchase_model = FB(data_user_byday.iloc[:-30])

def FPPredict(data,m):
    df = pd.DataFrame({
    'ds': data.report_date,
    'y': data.total_purchase_amt,
    })
#     df['cap'] = data.total_purchase_amt.values.max()
#     df['floor'] = data.total_purchase_amt.values.min()
    df_predict = m.predict(df)
    df['yhat'] = df_predict['yhat'].values
    df = df.set_index('ds')
    df.plot()
    return df

purchase_df = FPPredict(data_user_byday.iloc[-30:],purchase_model)

赎回

#定义模型
def FB(data: pd.DataFrame):
    df = pd.DataFrame({
    'ds': data.report_date,
    'y': data.total_redeem_amt,
    })
    df['cap'] = data.total_purchase_amt.values.max()
    df['floor'] = data.total_purchase_amt.values.min()
    m = prophet.Prophet(
        changepoint_prior_scale=0.05, 
        daily_seasonality=False,
        yearly_seasonality=True, #年周期性
        weekly_seasonality=True, #周周期性
        growth="logistic",
    )
#     m.add_seasonality(name='monthly', period=30.5, fourier_order=5, prior_scale=0.1)#月周期性
    m.add_country_holidays(country_name='CN')#中国所有的节假日    
    m.fit(df)
    future = m.make_future_dataframe(periods=30, freq='D')#预测时长
    future['cap'] = data.total_purchase_amt.values.max()
    future['floor'] = data.total_purchase_amt.values.min()
    forecast = m.predict(future)
    fig = m.plot_components(forecast)
    fig1 = m.plot(forecast)
    return forecast

result_redeem = FB(data_user_byday)

Bonus 时间序列特征工程

https://www.heywhale.com/mw/project/63904f5658e3bea6a3e52800

EDA

import sweetviz as sv

def eda(df, name, target=None):
    sweet_report = sv.analyze(df, target_feat=target)
    sweet_report.show_html(f'{name}.html')


def eda_compare(df1, df2, name, feature, target):
    feature_config = sv.FeatureConfig(force_text=feature, force_cat=feature)
    sweet_report = sv.compare(df1, df2, feat_cfg=feature_config, target_feat=target)
    sweet_report.show_html(f'{name}_compare.html')

完整版请访问：https://www.wolai.com/stupidccl/5dqha79nnrPMf5xTAs6jUu

参考资料

kaggle notebook: https://www.kaggle.com/code/stupidccl/time-serious-analysis-1/edit/run/107631286