计算机视觉图像处理常用方法汇总

1.数字图像处理基础

1.1 人眼图像的形成

1. 光线进入眼睛：当光线从一个物体反射或散射出来，进入人的眼睛时，它们通过角膜和晶状体进入眼球内部。
2. 聚焦光线：角膜和晶状体将光线聚焦在视网膜上。晶状体可以通过调整其形状来调节聚焦距离，使物体的图像清晰地映射在视网膜上。
3. 光敏细胞感受光线：视网膜是一层包含光敏细胞的组织，分为两种类型的细胞：锥状细胞和杆状细胞。锥状细胞负责颜色和明亮度感知，杆状细胞则负责在低光条件下感知。
4. 神经信号传递：光敏细胞受到光线刺激时，会产生神经信号，这些信号随后传递到视神经和大脑。在视神经和视皮层中，这些信号被进一步处理和解释，以形成我们所看到的视觉图像。

1.1 图像数字化

图像数字化是将图像转换为数字信号的过程。数字化图像通常由数字矩阵组成，每个元素表示图像上的一个像素，并用数字表示该像素的颜色和亮度。

数字化图像的过程通常包括以下步骤：

1. 采集：采集图像需要使用一种数字化设备，例如数码相机、扫描仪或摄像机。数字化设备将图像转换为数字信号，这些信号可以由计算机处理。
2. 采样：采样是将连续图像转换为离散像素的过程。数字化设备将图像分成网格，每个网格称为像素，采集每个像素的颜色和亮度信息，例如：一幅640480分辨率的图像，表示这幅图像是由640480=307200个点组成的。
3. 量化：量化是将每个像素的颜色和亮度值转换为数字值的过程。在量化过程中，将连续信号转换为离散信号。量化级别决定了数字图像中可以显示的颜色和亮度的数量。例如：一幅8位的图像，表示每个采样点有$2^8$=256级，从最暗到最亮，可以分辨为256个级别
4. 编码：编码是将数字化的像素值储存为数字格式的过程。编码格式通常包括JPEG、PNG、BMP等

对于一张彩色图片，这张图片的内容是由分辨率（示例：1920x1080）数量级的像素组成。类似于淘宝卖的钉子画，就是由1920乘以1080个钉子组成的画，其中每个钉子的颜色，是由三个通道（RGB）共同组成（三种分别叫R、G、B的钉子组成），

这三个通道像是我们学水彩绘画的中心三颜色（红黄蓝），通过这三种颜色可以调出不同的颜色
也可以理解为，三种通道为三种图层，图层与图层之间组成的颜色。

每一个通道下的每一个钉子的颜色，在计算机视角下就表示为一个0～255的值

既然知道了，在计算机科学的视角下，图片就是数值，那所谓的Opencv图像处理，P图，美颜等等功能，其实就是数值的变化，明白其中的数学公式和逻辑，Opencv的常用算法函数就清晰了。所以本文主要从数学线性代数的角度讲解算法方法。

1.2 图像的种类

按照图像在视觉或设备中的成像效果，可以将图像分为：

1. 灰度图：也就是常说的黑白照片，单通道
2. 彩色图像：RGB、HSV、YUV、CMYK、Lab

通常我们做特定颜色检测的时候，一般选择用HSV空间的图像，下面一个实例，可以自我调整HSV的数值，来获取在图像中自己想要的颜色。

1.2.1 颜色分割

做颜色特征检测，需要将我们的图片RGB模式转化为HSV模式，H：色彩，S：饱和度，V：明度

下面的代码，我们可以通过调节滑块中HSV的值来观察图片中的颜色变化。

createTrackbar是Opencv中的API，其可在显示图像的窗口中快速创建一个滑动控件，用于手动调节阈值，具有非常直观的效果
cv2.createTrackbar(trackbarName, windowName, value, count, onChange)创建滑动条函数

• trackbarName：滑动空间的名称；
• windowName：滑动空间用于依附的图像窗口的名称；
• value：初始化阈值；
• count：滑动控件的刻度范围；最小值默认为0。
• onChange：回调函数（所谓回调函数即每次修改滑动条后，需要传入新变量的函数）的名称

cv2.getTrackbarPos获取滑动条位置处的值

import cv2
import numpy as np

#定义HSV滑块的值
def empty(a):
    h_min = cv2.getTrackbarPos("Hue Min","TrackBars")
    h_max = cv2.getTrackbarPos("Hue Max", "TrackBars")
    s_min = cv2.getTrackbarPos("Sat Min", "TrackBars")
    s_max = cv2.getTrackbarPos("Sat Max", "TrackBars")
    v_min = cv2.getTrackbarPos("Val Min", "TrackBars")
    v_max = cv2.getTrackbarPos("Val Max", "TrackBars")
    print(h_min, h_max, s_min, s_max, v_min, v_max)
    return h_min, h_max, s_min, s_max, v_min, v_max

#图片拼接，将4张图片拼接到一起
def stackImages(scale,imgArray):
    rows = len(imgArray)
    cols = len(imgArray[0])
    rowsAvailable = isinstance(imgArray[0], list)
    width = imgArray[0][0].shape[1]
    height = imgArray[0][0].shape[0]
    if rowsAvailable:
        for x in range ( 0, rows):
            for y in range(0, cols):
                if imgArray[x][y].shape[:2] == imgArray[0][0].shape [:2]:
                    imgArray[x][y] = cv2.resize(imgArray[x][y], (0, 0), None, scale, scale)
                else:
                    imgArray[x][y] = cv2.resize(imgArray[x][y], (imgArray[0][0].shape[1], imgArray[0][0].shape[0]), None, scale, scale)
                if len(imgArray[x][y].shape) == 2: imgArray[x][y]= cv2.cvtColor( imgArray[x][y], cv2.COLOR_GRAY2BGR)
        imageBlank = np.zeros((height, width, 3), np.uint8)
        hor = [imageBlank]*rows
        hor_con = [imageBlank]*rows
        for x in range(0, rows):
            hor[x] = np.hstack(imgArray[x])
        ver = np.vstack(hor)
    else:
        for x in range(0, rows):
            if imgArray[x].shape[:2] == imgArray[0].shape[:2]:
                imgArray[x] = cv2.resize(imgArray[x], (0, 0), None, scale, scale)
            else:
                imgArray[x] = cv2.resize(imgArray[x], (imgArray[0].shape[1], imgArray[0].shape[0]), None,scale, scale)
            if len(imgArray[x].shape) == 2: imgArray[x] = cv2.cvtColor(imgArray[x], cv2.COLOR_GRAY2BGR)
        hor= np.hstack(imgArray)
        ver = hor
    return ver



path = '1.jpg'
cv2.namedWindow("T
# 创建一个窗口，放置6个滑动条rackBars")
cv2.resizeWindow("TrackBars",640,240)
cv2.createTrackbar("Hue Min","TrackBars",0,179,empty)
cv2.createTrackbar("Hue Max","TrackBars",19,179,empty)
cv2.createTrackbar("Sat Min","TrackBars",110,255,empty)
cv2.createTrackbar("Sat Max","TrackBars",240,255,empty)
cv2.createTrackbar("Val Min","TrackBars",153,255,empty)
cv2.createTrackbar("Val Max","TrackBars",255,255,empty)

while True:
    img = cv2.imread(path)
    imgHSV = cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
    # 调用回调函数，获取滑动条的值
    h_min = cv2.getTrackbarPos("Hue Min","TrackBars")
    h_max = cv2.getTrackbarPos("Hue Max", "TrackBars")
    s_min = cv2.getTrackbarPos("Sat Min", "TrackBars")
    s_max = cv2.getTrackbarPos("Sat Max", "TrackBars")
    v_min = cv2.getTrackbarPos("Val Min", "TrackBars")
    v_max = cv2.getTrackbarPos("Val Max", "TrackBars")
    lower = np.array([h_min,s_min,v_min])
    upper = np.array([h_max,s_max,v_max])
    # 获得指定颜色范围内的掩码
    mask = cv2.inRange(imgHSV,lower,upper)
    # 对原图图像进行按位与的操作，掩码区域保留
    imgResult = cv2.bitwise_and(img,img,mask=mask)


    # cv2.imshow("Original",img)
    # cv2.imshow("HSV",imgHSV)
    # cv2.imshow("Mask", mask)
    # cv2.imshow("Result", imgResult)

    imgStack = stackImages(0.6,([img,imgHSV],[mask,imgResult]))
    cv2.imshow("Stacked Images", imgStack)

    cv2.waitKey(1)

1.3 像素之间的关系

数字图像在计算机视觉下，实际上是一个矩阵的形状

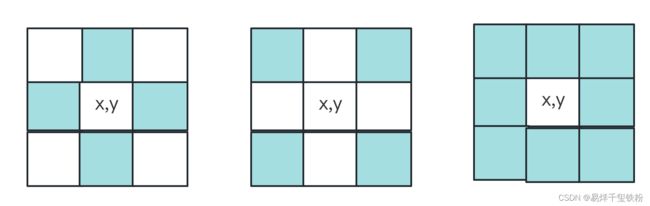
像素的下标又被称为坐标(x,y)，我们可以从坐标的信息中发现像素与像素之间存在着一些空间位置的关系

1.3.1 领域

• 4-领域 ：对于坐标(x,y)的像素P，P有四个水平垂直的相邻像素，称为4-领域$(x-1,y),(x+1,y),(x,y-1),(x,y+1)$
• 对角领域 ：P有四个对角相邻像素，$(x-1,y-1),(x-1,y+1),(x+1,y-1),(x+1,y+1)$
• 8-领域：4-领域和对角领域合称为像素的8-领域

1.3.2 连接和连通

如果两个像素不仅空间上位置上领接，并且其他像素值也符合相似准则，则二个像素是连接的。
像素相似准则，指像素的灰度值相等，或者说像素值都在一个灰度集合中v中。

举例说明，8级灰度，像素值的范围在0～256（$2^8$）,7级灰度的像素值范围在0~128，那7级到8级这128～256范围的像素值就是一个灰度集合。

• 4-连接 ：像素p,q都在集合v中的取值，并且q,p互为4-领域
• 8-连接 ：像素p,q都在集合v中的取值，并且q,p互为8-领域
• 像素连通：就是在连接的基础上，增加的概念。如果说对于同个像素点存在：p和q连接、q和r连接，r和s连接，s和t连接，则p和t连通。
• 
  如果说连通的线，形成闭合环的，也可以叫连通域。
  

图像处理的算法技术，正是运用了像素之间的空间位置关系和像素数值，结合多种数学、线性代数逻辑实现，图像效果变化的。

2.图像预处理技术

图像处理的输入和输出形式，有以下几种形式：

输入	输出
单幅图像	单幅图像
多幅图	单幅图像
单幅图	数字或符号等内容
多幅图	数字或符号等内容

图像预测处理主要目的是消除图像中无关的信息，提取出有用信息（很像做结构数据的特征提取），来增加有关信息的可检测性，最大限度地简化数据，从而改进特征提取，图像分割、匹配和识别的可靠性，并应用到深度学习分析预测中，具体流程可以如下

图像预测处理流程主要包括：灰度变换、几何变换、图像增强、图像滤波等等

2.1 灰度变换

灰度变换是指将一幅图像的像素灰度值进行一定的映射变换，使得图像的亮度、对比度或颜色得到调整，以达到某种特定的视觉效果。

我们记录像素点的原始值为s，灰度变换的映射函数为T(s)，变换后的像素点为d，即：
$$d=T(s)$$
下面介绍几种常见的图像处理灰度变换方法：

2.1.1 线性变换

线性变换是一种简单的灰度变换方法，它将图像的灰度值进行线性映射，通常用下面的公式来表示：

$$g(x,y)=a\ast f(x,y)+b$$

其中，$f(x,y)$表示原图像的灰度值，$g(x,y)$表示变换后的灰度值，a和b是常数，可以通过调整它们来控制变换的幅度和方向。

2.1.2 对数变换

对数变换可以增强图像的暗部细节，通常用下面的公式来表示：

$$g(x,y)=c\ast log(1+f(x,y))$$

其中，$f(x,y)$表示原图像的灰度值，$g(x,y)$表示变换后的灰度值，$c$是常数，可以通过调整它来控制变换的幅度。

2.1.3 幂律变换

幂律变换可以增强图像的亮部细节，通常用下面的公式来表示：

$$g(x,y)=c\ast f(x,y{)}^{\gamma }$$

其中，$f(x,y)$表示原图像的灰度值，$g(x,y)$表示变换后的灰度值，$c$和$\gamma$是常数，可以通过调整它们来控制变换的幅度和方向。

2.1.4 反转

反转是一种简单的灰度变换方法，它可以将图像中亮度值较高的区域变暗，将亮度值较低的区域变亮，从而实现对比度的增强。反转的实现方法很简单，只需要将每个像素的灰度值取反即可。例如，原图像中的像素灰度值为g，反转后的像素灰度值为255-g。

2.1.5 对比度增强

对比度增强是一种将图像中的灰度值重新映射到更广的范围内，从而增加图像的对比度的方法。对比度增强的实现方法有很多种，其中一种常用的方法是灰度拉伸，具体来说：

假设原图像的像素值范围为[a,b]，将其线性拉伸到[0,255]的范围内，拉伸函数可以表示为：

$$g(x)=\frac{(x-a)\times 255}{b-a},x\in [a,b]$$

其中，$x$为原图像的像素值，$g(x)$为拉伸后的像素值。

在OpenCV中，也可以使用LUT（查找表）来实现灰度拉伸。

具体步骤如下：
（1）计算拉伸函数$g(x)$，其中$x\in [a,b]$，$a$和$b$分别为原图像的最小像素值和最大像素值。$$g(x)=\frac{(x-a)\times 255}{b-a}$$
（2）创建一个$256$个元素的查找表$lookup$，其中$lookup(i)$表示原图像中像素值为$i$的像素在拉伸后的像素值。
（3）遍历原图像的每个像素，查找表中查找对应的新像素值，将其赋值给输出图像。

下面是使用LUT实现灰度拉伸的代码示例：

import cv2
import numpy as np

# 读取原图像
img = cv2.imread('test.jpg', cv2.IMREAD_GRAYSCALE)

# 计算拉伸函数
a = np.min(img)
b = np.max(img)
g = lambda x: (x-a)*255/(b-a)

# 创建查找表
lookup = np.zeros(256, dtype=np.uint8)
for i in range(256):
    lookup[i] = np.clip(g(i), 0, 255)

# 使用查找表进行灰度拉伸
img_stretched = cv2.LUT(img, lookup)

# 显示原图像和拉伸后的图像
cv2.imshow('Original Image', img)
cv2.imshow('Stretched Image', img_stretched)
cv2.waitKey(0)
cv2.destroyAllWindows()

在这个示例中，我们使用np.clip()函数将像素值限制在$[0,255]$范围内，以避免输出像素值超出范围的问题。

2.1.6 对比度压缩

对比度压缩是一种将图像中的灰度值重新映射到更窄的范围内，从而减少图像的对比度的方法。对比度压缩的实现方法也有很多种，其中一种常用的方法是对数变换。具体来说，对数变换将图像中的灰度值取对数后再缩放到[0,255]范围内，公式如下：

$$g(x)=\frac{(x-a)\times 255}{b-a},x\in [a,b]$$其中，$x$为原图像的像素值，$g(x)$为压缩后的像素值。

在OpenCV中，可以使用LUT（查找表）来实现对比度压缩。具体步骤如下：
（1）计算压缩函数$g(x)$，其中$x\in [a,b]$，$a$和$b$分别为压缩后的最小像素值和最大像素值。$$g(x)=\frac{(x-a)\times 255}{b-a}$$
（2）创建一个$256$个元素的查找表$lookup$，其中$lookup(i)$表示原图像中像素值为$i$的像素在压缩后的像素值。
（3）遍历原图像的每个像素，查找表中查找对应的新像素值，将其赋值给输出图像。

下面是使用LUT实现对比度压缩的代码示例：

import cv2
import numpy as np

# 读取原图像
img = cv2.imread('test.jpg', cv2.IMREAD_GRAYSCALE)

# 计算压缩函数
a = 50
b = 200
g = lambda x: (x-a)*255/(b-a)

# 创建查找表
lookup = np.zeros(256, dtype=np.uint8)
for i in range(256):
    lookup[i] = np.clip(g(i), 0, 255)

# 使用查找表进行对比度压缩
img_compressed = cv2.LUT(img, lookup)

# 显示原图像和压缩后的图像
cv2.imshow('Original Image', img)
cv2.imshow('Compressed Image', img_compressed)
cv2.waitKey(0)
cv2.destroyAllWindows()

2.1.7 伽马矫正

伽马矫正是一种通过对图像中的灰度值进行非线性变换，从而调整图像亮度的方法。伽马矫正的原理是通过一个非线性函数来映射原图像中的灰度值，从而使得亮度值更低的区域变暗，亮度值更高的区域变亮。具体来说，伽马矫正使用下面的公式进行灰度值变换：

$$g^{=}A{g}^{\gamma }$$

其中，g表示原图像中的像素灰度值，g’表示伽马矫正后的像素灰度值，A和γ是参数。A控制了灰度值的幅度，通常情况下A=1，γ控制了灰度值变化的速度，通常情况下γ取值范围在[0.5, 2.5]之间。当γ小于1时，图像中的亮度值较低的区域将被放大，从而提高了图像的对比度；当γ大于1时，图像中的亮度值较高的区域将被放大，从而使图像更加明亮。

反转、对比度增强、对比度压缩和伽马矫正是常用的图像灰度变换方法，它们可以用于调整图像的亮度、对比度等属性。根据实际需要选择合适的灰度变换方法可以改善图像的视觉效果，提高图像分析和处理的效果。

2.2 图像直方图

图像直方图：直方图，是指对整个图像在灰度范围内的像素值(0~255)统计出现频率次数，据此生成的直方图，称为图像直方图。直方图反映了图像灰度的分布情况。是图像的统计学特征，

如果我们使用RBG分别对三个通道实现直方图，就那这三个直方图就代表这个图像的特征。

2.2.1 直方图均衡化

直方图均衡化是一种更为高级的增强图像对比度的方法，其基本思想是通过对图像的像素值进行变换，使得像素值在整个灰度范围内分布均匀，从而增强图像的对比度。

均衡化转化

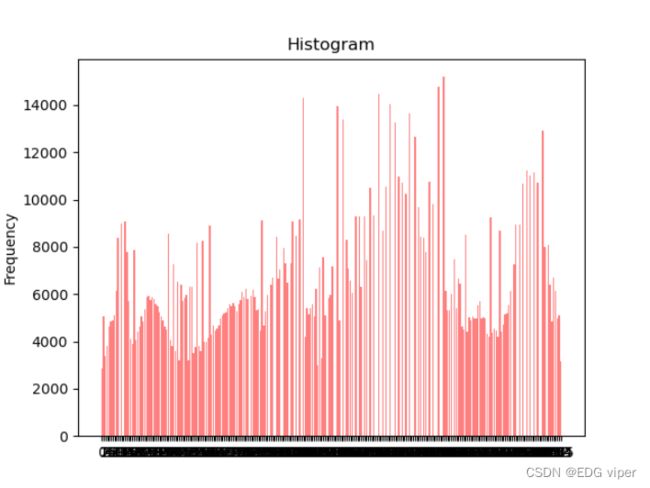
可以看到均衡化，是将直方图中的内容左右拉伸了一下。（让图像中像素领域之间差异显得不大，平衡整个图片的色彩，使我们观察图片，不会发现某个地方色彩对比其他位置突出）

直方图均衡化：直方图均衡化是一种常见的图像增强方法，它通过对图像的灰度直方图进行均衡化，使得图像的亮度分布更加均匀，从而增强图像的对比度和细节。具体实现方法可以参考以下步骤：

（1）计算原图像的灰度直方图；
（2）计算灰度直方图的累积分布函数；
（3）根据累积分布函数对原图像进行灰度值映射；
（4）得到均衡化后的图像。

具体而言，假设原图像的像素值范围为[0,255]，其灰度直方图为$H(i),i\in [0,255]$，CDF为$C(i),i\in [0,255]$，均衡化后的像素值为$g(i),i\in [0,255]$，则有：$$C(i)=\sum _{j=0}^{i}H(j)$$$$g(i)=\lfloor \frac{255\times C(i)}{MN}\rfloor$$其中，$M$和$N$分别为原图像的宽度和高度。在OpenCV中，可以使用equalizeHist()函数来实现直方图均衡化。需要注意的是，直方图均衡化有时会导致图像的噪声增强，因此在实际应用中需要谨慎使用。

2.3 空间滤波

空间滤波是一种基于图像局部邻域像素的图像处理方法，它通过对图像像素周围的邻域像素进行加权平均或其他数学运算来改变图像的特征。

空间滤波在图像去噪、边缘检测、图像增强等方面有着广泛的应用。

常见的空间滤波算法包括均值滤波、中值滤波、高斯滤波等。

• 均值滤波：将像素点周围的邻域像素的灰度值进行平均，用来减少图像中的噪声。
• 中值滤波：用邻域像素的中值来代替当前像素值，可以有效地去除图像中的椒盐噪声等非线性噪声。
• 高斯滤波：将邻域像素的灰度值按照一定的权值进行加权平均，其中权值由高斯函数计算得到，可以有效地平滑图像并保留较好的图像细节。

空间滤波的一般步骤如下：

1. 定义一个固定大小的滤波器（也称为卷积核或模板），滤波器通常是一个矩阵。
2. 将滤波器中心对准当前像素，将滤波器中的所有元素与当前像素的邻域像素进行加权或其他数学运算，得到当前像素的输出值。
3. 移动滤波器，重复步骤2，直到所有像素都被处理过。

使用不同的滤波（卷积核也就是矩阵）来实现图像像素的改变，其中的主要有三功能分别是图像的模糊/去噪、图像梯度/边缘发现、图像锐化/凸图像增强，我这里都把这些功能都看成是图像增强， 因为这些操作都是修改了图像的像素。

使用滤波增强强调图像中感兴趣的部分，增强图像的高频成分，可以使图像中物体的轮廓清晰，细节清晰； 增强低频分量可以降低图像中噪声的影响，（对图像中的像素值进行处理），也可以是使图像变得模糊。

2.3.1 均值滤波

均值滤波是指用当前像素点周围N*N个像素点的均值来代替当前像素值

$\frac{112\ast 6+110\ast 4+60\ast 8+6\ast 70}{24}=83.33$

2.3.2 方框滤波

方框滤波不会计算像素均值，它可以自由选择是否对均值滤波的结果进行归一化，即可以自由选择滤波结果是邻域像素值之和的平均值，还是邻域像素值之和。

2.3.3 高斯滤波

在进行均值滤波与方框滤波时，其邻域内每个像素的权重是相等的。而高斯滤波会将中心点的权重加大，远离中心点的权重减小，以此来计算邻域内各个像素值不同权重的和。

2.3.4 中值滤波

用邻域内所有像素值的中间值来代替当前像素点的像素值。

2.3.5 双边滤波

双边滤波是一种非线性的滤波方法，它在平滑图像的同时保留了边缘信息。其核心思想是通过对像素点的空间位置和像素值之间的相似度进行加权平均，来达到滤波的效果。

双边滤波公式为：

其中，$I_{filtered}(x,y)$表示滤波后的像素值，$I(i,j)$表示邻域像素$(i,j)$的灰度值，$f_p(i,j)$表示像素$(i,j)$与中心像素$(x,y)$的相似度，$w_s$和$w_r$分别表示空间权值和像素值权值，$W_p(x,y)$是归一化的权值之和，用于保证滤波后像素值的范围在$[0,255]$之间。

在实际应用中，$f_p(i,j)$通常使用高斯函数来计算，空间权值$w_s$和像素值权值$w_r$也可以使用高斯函数来计算，它们的值都取决于两个参数，分别是空间域参数和灰度域参数。空间域参数决定了滤波器的半径，灰度域参数决定了滤波器对灰度差异的敏感程度。

2.3.6 边缘锐化

图像梯度计算的是图像变化的速度

对于图像的边缘部分，其灰度值变化较大，梯度值也较大；相反，对于图像中比较平滑的部分，其灰度值变化较小，相应的梯度值也较小。一般情况下，图像的梯度计算是图像的边缘信息。

其实梯度就是导数，但是图像梯度一般通过计算像素值的差来得到梯度的近似值，也可以说是近似导数。该导数可以用微积分来表示。

在线性代数微积分中，一维函数一阶微分定义：
$$\frac{df}{dx}=\underset{ϵ\to 0}{\lim }\frac{f(x+ϵ)-f(x)}{ϵ}$$

在图像中就是一个二维函数$f(x,y)$，有二个方向，一个x方向一个y方向，因此需要做偏微分：
$$\frac{\partial f(x,y)}{\partial x}=\underset{ϵ\to 0}{\lim }\frac{f(x+ϵ,y)-f(x,y)}{ϵ}$$
$$\frac{\partial f(x,y)}{\partial y}=\underset{ϵ\to 0}{\lim }\frac{f(x,y+ϵ)-f(x,y)}{ϵ}$$

那个这个二维函数总的梯度就为：
$$G=\sqrt{(\frac{\partial f(x,y)}{\partial x}{)}^2+(\frac{\partial f(x,y)}{\partial y}{)}^2}$$

每一个像素的梯度是由它周围8个像素共同确定的

要想计算出图像的边缘的基本特征，就需要类似的空间滤波，在这里空间滤波也叫它算子，主要用于计算边缘的算子有Sobel、Robort、Laplacian。

Sobel算子

Sobel X方向算子模版：

G x = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] (2) G_x=\left[ \begin{matrix} -1 & 0 & +1\\ -2 & 0 & +2\\ -1 & 0 & +1\\ \end{matrix} \right] \tag{2} Gx​= ​−1−2−1​000​+1+2+1​ ​(2)

Sobel y方向算子模版：
G y = [ − 1 − 2 − 1 0 0 0 + 1 + 2 + 1 ] (3) G_y=\left[ \begin{matrix} -1 & -2 & -1\\ 0 & 0 & 0\\ +1 & +2 & +1\\ \end{matrix} \right] \tag{3} Gy​= ​−10+1​−20+2​−10+1​ ​(3)

Robort算子

Robort 算子模版
$$G=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\text{\hspace{1em}(4)}$$$$G_{=}\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\text{\hspace{1em}(4)}$$

矩阵与矩阵相乘，比如 一个$m\ast n$和一个$r\ast c$一定要$n=r$才能发生，
已知我们的算子是$2\ast 2$，对应到需要变化的图像上，也一定是取$m\ast 2$的形状，去算子相乘，但最好是与算子形状相同。

转

Laplacian算子

Laplacian算子是基于二阶微分计算的，其定义如下：

$$G=\frac{{\partial }^{2}f(x,y)}{\partial x^2}+\frac{{\partial }^{2}f(x,y)}{\partial y^2}$$

其中：
$\frac{{\partial }^{2}f(x,y)}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)$
$\frac{{\partial }^{2}f(x,y)}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y)$

Laplacian算子模版
G = [ 0 1 0 1 − 4 1 0 1 0 ] (4) G_=\left[ \begin{matrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 &0 \end{matrix} \right] \tag{4} G=​ ​010​1−41​010​ ​(4)

2.4 坐标变换

图像的坐标变换又被称为图像的几何计算，常见的基本变换有：图像平移、镜像、缩放、旋转、仿射

常用于深度学习。数据增强

cv2.warpAffine() 仿射变换

dst = cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]])

• src：输入图像
• M：2*3 transformation matrix (转变矩阵)
• dsize：输出图像的大小，格式为(cols,rows)，width 对应 cols，height 对应 rows
• flags： 可选参数，插值方法的组合（int 类型），默认值 INTER_LINEAR
• borderMode：可选参数，边界像素模式（int 类型），默认值 BORDER_CONSTANT
• borderValue：可选参数，边界填充值; 默认情况下，默认值 Scalar()即 0

将图像看成是一个矩阵
warpAffine(img,M,(rows,cols)) 实现基本的仿射变换效果，但是这种情况会出现 黑边 现象。最后一个参数为 borderValue，边界填充的颜色，默认为黑色，M为一个转换矩阵，Opencv函数通过图像矩阵

2.4.1 图像平移

在图像平移动中$M$是一个转换矩阵：$$\left[\begin{array}{ccc}1& 0& dx\\ 0& 1& dy\end{array}\right]\text{\hspace{1em}(3)}$$

图像平移公式如下：其中 $dx$,$dy$ 表示在$(x,y)$方向上的位移，如下所示：：

2.4.2 旋转

在图像旋转中$M$是一个转换矩阵：$$\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\end{array}\right]\text{\hspace{1em}(3)}$$

2.4.3 缩放

在图像缩放中$M$是一个转换矩阵：$$\left[\begin{array}{ccc}{S}_x& 0& 0\\ 0& S_y& 0\end{array}\right]\text{\hspace{1em}(3)}$$

2.4.4 镜像

设图像的大小为$m\ast n$

水平镜像，x位置不变，只反转y位置：
$${\alpha }_{x,y}={\alpha }_{x,n-y+1}$$

垂直镜像，y位置不变，只反转x位置：
$${\alpha }_{x,y}={\alpha }_{m-x+1,y}$$

对角镜像，x，y位置都反转
$${\alpha }_{x,y}={\alpha }_{m-x+1,n-y+1}$$

2.4.5 图像矫正

matrix = cv2.getPerspectiveTransform(pts1,pts2)
imgOutput = cv2.warpPerspective(img,matrix,(width,height))

2.4.6 图像缩放

在opencv中我们用图像金字塔用来进行图像缩放的，与resize函数类似
其中图像金字塔根据方法可以分成为：
高斯金字塔：缩小图像也叫下采样，用PryDown函数
拉普斯金字塔：放大图像也叫上采样，用PryUp函数

2.5 图像插值

线性插值法，所有方法都采用同一种插值内核，不用考虑待插像素点所处的位置，这种方法会使用图像中边缘模糊

在对二维数据进行 resize 操作时，经常会将原本的整数坐标变换为小数坐标，对于非整数的坐标值一种直观有效的插值方式为双线性插值。

2.5.1 最近邻插值

算法思想：插值的目的是根据已知的图像的像素值获得未知目标图像的像素值，插值变换过程如下图

假设原始图像（矩阵），每个像素点位置表示为$sr{c}_x,sr{c}_y$，$ta{g}_x,ta{g}_y$表示插值得到的目标像素点位置坐标。

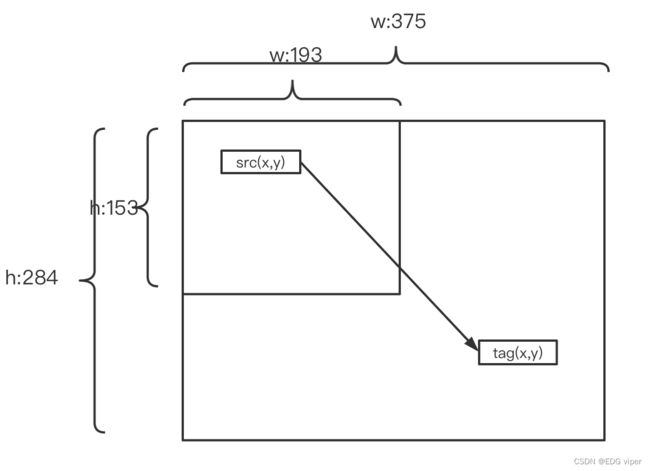
如何得到tag的位置由如下公式：

src图像：
w:193 h:153
tag图像：
w:375 h:284

首先获得原始图像与目标图像的映射关系
$rati{o}_w=\frac{ta{g}_w}{sr{c}_w}=\frac{ta{g}_x}{sc{r}_x}=\frac{375}{193}$
$rati{o}_h=\frac{ta{g}_h}{sr{c}_h}=\frac{ta{g}_y}{sc{r}_y}=\frac{284}{153}$

通过映射值，得到tag的坐标位置
$ta{g}_x=int(sr{c}_x\ast rati{o}_w)$
$ta{g}_y=int(sr{c}_y\ast rati{o}_h)$

就可以把$sr{c}_{(}x,y)$位置的像素值赋值给$ta{g}_{(}x,y)$

2.5.2 单线性插值

如上图所示，在红色块中间插一个蓝色像素块

二点之间求一条直线，这二点之间任意一点，都落在这个直线上，三点之间任意二点斜率相同

$\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}$

整理一下
$y=\frac{x_2-x}{x_2-x_1}{y}_1+\frac{x-x_1}{x_2-x_1}{y}_2$

计算蓝色块像素值公式如下：

$$f(x,y)=\frac{x_2-x}{x_2-x_1}f(x_1,y_1)+\frac{x-x_1}{x_2-x_1}f(x_2,y_2)$$

2.5.3 双线性插值

又上图，解释，我们可以通过红色的像素块，实现线性插值，得到蓝色和绿色的像素块的像素值，具体公式如下：

先计算蓝色像素块的，其中x，x1，x0，就是像素块在矩阵中的位置坐标，y同理也是：

$$f(x,y_0)=\frac{x_1-x}{x_1-x_0}f(x_0,y_0)+\frac{x-x_0}{x_1-x_0}f(x_1,y_0)$$
$$f(x,y_1)=\frac{x_1-x}{x_1-x_0}f(x_0,y_1)+\frac{x-x_0}{x_1-x_0}f(x_1,y_1)$$

再计算绿色块的像素
$$f(x,y)=\frac{y_1-y}{y_1-y_0}f(x,y_0)+\frac{y-y_0}{y_1-y_0}f(x,y_1)$$

2.5.4 双三次

目标图像中每一个像素由原图上相对应点周围的4x4=16个像素的灰度值进行加权，得到一个更接近高分辨率图像的放大效果。

行X轴方向上的4个红色像素块距离绿色像素块距离分别：2，1，-1，-2
行Y轴方向上的4个红色像素块距离绿色像素块距离分别：2，1，-1，-2

如果想得到绿色像素块(x,y)的值，根据源图像距离像素(x,y)最近的16个像素点作为计算绿色像素块(x,y)处像素值的参数，利用BiCubic基函数求出16个像素点的权重，绿色像素(x,y)的值就等于16个像素点的加权叠加。

BiCubic函数中的参数x表示该像素点到目标像素点的距离，例如（x-2,y-2）距离(x,y)的距离为(2,2)，因此(x-2,y-2)的横坐标权重为W(2)，纵坐标权重W(2)。

BiCubic权重公式如下
$$S(x)=\{\begin{array}{l}1-2|x{|}^2+x^3,|x|<1\\ 4-8|x|+5|x{|}^2-|x{|}^3,1\le |x|<2\\ 0,|x|\ge 2\end{array}\text{\hspace{1em}()}$$

求(x,y)像素值的公式：

$$f(x,y)=AB{C}^T$$
$$A=[S(2)S(1)S(-1)S(-2)]$$
$$B=Src[x-1:x+1,y-1:y+1]$$
$$C=[S(2)S(1)S(-1)S(-2)]$$

2.6 仿射变换

图像仿射变换是指将一个二维平面上的点通过一组线性变换映射到另一个二维平面上的点，从而实现对图像的旋转、平移、缩放等操作。它可以表示为如下矩阵形式的线性变换：

2.7 数据增强处理

数据增强是指通过一系列图像处理技术来扩充数据集，从而提高模型的泛化能力和鲁棒性。彩色图像的数据增强一般包括以下几种：

1. 色彩变换：改变图像的颜色，例如改变图像的色调、饱和度和亮度等。色彩变换可以使得模型对颜色的变化更加鲁棒。
2. 几何变换：改变图像的几何结构，例如随机裁剪、旋转、翻转等。几何变换可以使得模型对于物体的位置、角度等变化更加鲁棒。
3. 噪声添加：向图像中添加噪声，例如高斯噪声、椒盐噪声等。噪声添加可以使得模型对于图像噪声的影响更加鲁棒。
4. 图像重构：将图像分解为不同的频率分量，对每个分量进行增强处理，然后将分量合成为一个新的图像。图像重构可以使得模型对于图像的细节和纹理更加鲁棒。
5. 对比度增强：增强图像的对比度，使得图像的亮度和色彩更加鲜明。对比度增强可以使得模型更加容易区分不同的物体。

3. 图像特征提取

图像特征提取是指从图像中提取出有用的、可表示图像的特征。图像特征通常由像素值或像素值的组合构成，例如边缘、角点、纹理等。常用的特征提取方法包括：颜色直方图、梯度直方图、局部二值模式（LBP）等。这些方法都是通过对图像像素值进行统计或计算，从而获得对图像的描述。

与图像预处理相比，特征提取更加注重从图像中提取有用的信息，为后续的图像分类、目标检测、图像识别等任务提供有效的输入。图像预处理主要是对原始图像进行降噪、尺度变换、旋转、裁剪等操作，从而更好地适应于特定的应用场景。

在深度学习中，图像特征提取是一个非常关键的步骤。传统的图像特征提取方法需要手动选择特征，比较依赖于人工经验。而基于深度学习的图像特征提取可以利用卷积神经网络（CNN）等深度学习模型，自动学习图像特征，避免了手动特征选择的过程。这种基于深度学习的图像特征提取方法已经在图像分类、目标检测、图像分割等任务中取得了非常好的效果，并成为当前图像处理领域的研究热点之一。

3.1 图像二值化

图像二值化 (image binarization）是将图像上的像素点的灰度值全部设置为黑色 (0)
或白色（255） ，也就是将整个图像分割成明显的黑白效果的过程。

其中最常用的是阈值分割，将图像中灰度值大于國值的像素点设置为白色（或黑色），小于國值的点设置为黑色（或白色），阈值 （Threshold）通常用T表示。

另外由于阈值选取直接影响了二值化分割效果自适应阈值分割，如何选择合适的阈值是算法的核心，因此有一种通过算法自动计算出分割阈值方法叫自适应阈分割

常见的自适应阈值分割有双峰法和最大类间方差法（OTSU）

3.1.1 双峰法

双峰法假定图像的灰度直方图是由两个峰值组成的。通过寻找直方图的两个峰值点，将它们的中间值作为阈值进行二值化。该方法适用于具有明显双峰分布的图像。

算法步骤：

对图像进行灰度化处理，获取灰度直方图。寻找灰度直方图的两个峰值点。将两个峰值点的中间值作为阈值进行二值化。

公式：
设 $h(i)$ 为灰度值为 $i$ 的像素点个数，$p$ 为灰度值为 $i$ 的像素点占总像素点数的比例，则灰度直方图的均值 $\mu$ 和方差 ${\sigma }^2$ 可以表示为：$$\mu =\sum _{i=0}^{L-1}i\cdot p(i)$$$${\sigma }^2=\sum _{i=0}^{L-1}(i-\mu {)}^2\cdot p(i)$$其中，$L$ 表示灰度级数。

3.1.2 最大类间方差法

最大类间方差法是一种自适应阈值的方法，它能够根据图像的局部灰度分布来自动选择合适的阈值。

算法原理：

最大类间方差法的核心思想是将图像分成两类，使得这两类之间的方差最大。方差越大，说明两类之间的差异越明显，因此选择的阈值也越合适。

具体实现步骤如下：

1. 统计图像的灰度直方图，得到每个灰度级的像素数量。
2. 计算每个灰度级的权重，即该灰度级所占总像素数的比例。
3. 从灰度级为1开始，循环计算每个灰度级的类间方差，即用该灰度级将图像分成两类后，两类之间的方差。方差计算公式为：$${\sigma }^2={\omega }_1({\mu }_1-{\mu }_t{)}^2+{\omega }^2({\mu }_2-{\mu }_t{)}^2{\sigma }^2={\omega }_1({\mu }_1-{\mu }_t{)}^2+{\omega }_2({\mu }_2-{\mu }_t{)}^2$$其中，${\omega }_1$和${\omega }_2$分别为两类像素占总像素数的比例，${\mu }_1$和${\mu }_2$分别为两类像素的平均灰度值，${\mu }_t$为总平均灰度值。
4. 找到类间方差最大的灰度级作为阈值，即为图像的自适应阈值。

公式：

最大类间方差法的计算公式为：$${\sigma }^2={\omega }_1({\mu }_1-{\mu }_t{)}^2+{\omega }^2({\mu }_2-{\mu }_t{)}^2{\sigma }^2={\omega }_1({\mu }_1-{\mu }_t{)}^2+{\omega }_2({\mu }_2-{\mu }_t{)}^2$$

其中，${\omega }_1$和${\omega }_2$分别为两类像素占总像素数的比例，${\mu }_1$和${\mu }_2$分别为两类像素的平均灰度值，${\mu }_t$为总平均灰度值。

3.2 形态学处理

腐蚀&膨胀是图像形态学的核心操作

腐蚀：对图像中的内容沿着边界，向内收缩（把图像中的线条变细，去掉一部分线条的像素值）
膨胀：对图像中的内容沿着边界，向内扩展（把图像中的线条变粗，增加一部分线条的像素值）

这两种操作的逻辑和作用都和上篇讲到的使用滤波器做平滑处理有些类似，不同之处在于，腐蚀求的是滤波核内像素的最小值，而膨胀求的是最大值。并将计算出的值复制给锚点位置的像素。

3.2.1 开运算&闭运算

开运算就是将图像先进性腐蚀操作，再进行膨胀操作。其可以用来抹除图像外部的细节(噪声)。

闭运算是先对图像进行膨胀操作，在进行腐蚀操作。其可以用来抹除图像的内部细节(噪声)。

腐蚀和膨胀虽然是逆操作，但是开运算和闭运算都不会使图像恢复原状。

3.3 特征描述子

特征描述子是图像处理和计算机视觉中一种用于描述图像局部特征的算法。它是一种将图像中的特征点表示为数学向量的技术，可以用于图像匹配、目标检测和识别等应用。

特征描述子的算法原理通常包括以下步骤：

1. 特征点检测：首先需要在图像中检测出具有独特性和区分度的局部特征点，例如角点、边缘、斑点等。
2. 特征点描述：对于每个特征点，需要计算其周围像素的特征值或特征向量，例如梯度方向、颜色、纹理等，用于描述该特征点的局部特征。
3. 特征点匹配：通过比较不同图像中的特征点描述子，可以进行特征点的匹配，用于图像配准、目标跟踪和识别等任务。

OpenCV提供了多种图像特征提取算法，并且支持多种特征描述子。
以下是一些常用的特征描述子：

• SIFT（Scale-Invariant Feature Transform）：尺度不变特征变换，是一种基于局部特征的描述子。SIFT描述子是通过计算关键点周围的梯度方向直方图来生成的，具有尺度不变性和旋转不变性。
• SURF（Speeded Up Robust Features）：SURF是SIFT的加速版，它采用了一些近似算法来加快计算速度，并具有与SIFT类似的尺度不变性和旋转不变性。
• ORB（Oriented FAST and Rotated BRIEF）：ORB是一种计算速度较快的特征描述子，它是基于FAST角点检测器和BRIEF二进制描述子的改进版本。ORB描述子具有旋转不变性和尺度不变性。
• HOG（Histogram of Oriented Gradients）：HOG是一种用于目标检测和分类的特征描述子。它是通过计算图像中的梯度方向直方图来生成的，具有方向性和尺度不变性。
• LBP（Local Binary Patterns）：LBP是一种局部特征描述子，它是通过计算图像中每个像素与其邻域像素之间的差异来生成的。LBP描述子具有旋转不变性和灰度不变性。