【建议收藏】机器学习数据预处理（二）——异常值处理方法（内附代码）

引言

大家好，我是生鱼同学。

今天我们继续进行异常值处理的方法介绍。

在获取到数据后，我们还需要处理由于不同原因而产生的异常值，这对于我们最后所构建模型有很大的帮助。

下面主要就介绍关于异常值的发现和处理方法。

和缺失值差不多，我们想要处理异常值，首先需要发现异常值。

发现异常值的方法也有很多种情况，接下来我们简单介绍几种常用的发现异常值的方法。

下面我将以天池学习赛中二手车项目的数据来作示范，可以私信我索要下载链接，或者访问我的其它相关文章，里面有相关的数据下载链接以及我对项目的理解和一些其它心得体会。

️根据统计结果进行分析

有些情况下，异常值是根据实际的业务逻辑中的数据的特性来决定其是否为异常的。例如一个人的体重不可能为负数且不可能过大。

其次，有些时候某些专业的属性也是存在着一定的范围的，例如某化合物的在水中的浓度肯定都存在一个饱和的临界点，超出这个点肯定是不正确的。

这部分就需要我们根据不同的业务逻辑和需求根据具体的情况分析。

下面我以二手车数据为例，分析其汽车功率的异常值情况：

# 复制原数据
pre_data = train_data.copy()
power = train_data['power']
# 获取到功率大于600的数据
power = list(power[power>600].index)
# 删除功率大于600的数据
train_data = train_data.drop(power, axis=0)

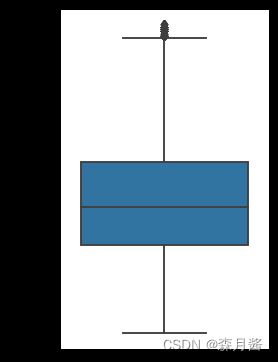
在本例中，题目明确提出功率的范围为[0:600]，所以我们编码判断哪部分的数据存在异常。接下来我们绘制删除前后的箱线图对比：

fig, ax = plt.subplots(1, 2, figsize=(10, 7))
sns.boxplot(y=pre_data['power'], data=pre_data, palette="Set1", ax=ax[0])
sns.boxplot(y=train_data['power'], data=train_data, palette="Set2", ax=ax[1])

在上图中，我们可以明显看出在删除之前存在很多异常值，甚至最高点已经达到了20000，这显然是不正确的数据，在删除之后数据便在题目所给的范围之内。

️根据 3δ原则分析

我们知道，世界上有很多东西都是服从正态分布的，这种方法就是根据正态分布的基本理而来。根据正态分布的定义可知，距离平均值3δ之外的概率为 P(|x-μ|>3δ) <= 0.003 ，这属于极小概率事件，我们就认为其超过这个范围的点为异常点。

这里我封装了一个函数来进行判断，判断的还是上述的power：

def sigema_3(data, col,sigema=3):
    # data: Dataframe数据
    # col：要处理的列名
    # sigema: 默认为3
    # return: 高于设定的索引和低于设定的索引
    mean = data[col].mean()
    std = data[col].std()
    fea = data[col]
    high_index = data[fea > mean + sigema * std].index
    low_index = data[fea < mean - sigema * std].index
    return high_index,low_index

sigema_3(train_data, 'power')

结果如下：

可以看到，这个方法显然不太适用于此数据，因为这样计算的话几乎删除了所有值。遂我们把sigema设定为1，然后绘制图来看一下：

import matplotlib.pyplot as plt

fig = plt.figure(figsize = (15,9))

ax1 = fig.add_subplot(2,1,1)
train_data['power'].plot(kind = 'kde',color = 'k',ylim = [0,0.005])
plt.axvline(mean-3*std,color = 'r',linestyle = '--')
plt.axvline(mean+3*std,color = 'r',linestyle = '--')

high_power = train_data[power > mean + 3 * std]
low_power = train_data[power < mean + 3 * std]

error = pd.concat([high_power,low_power], axis=0)

train_data.drop(error.index, axis=0, inplace=True)

ax2 = fig.add_subplot(2,1,2)
plt.scatter(train_data['power'].index, train_data['power'].values,color = 'k',alpha = 0.3)
plt.scatter(error.index,error['power'].values,color = 'r',alpha = 0.8)

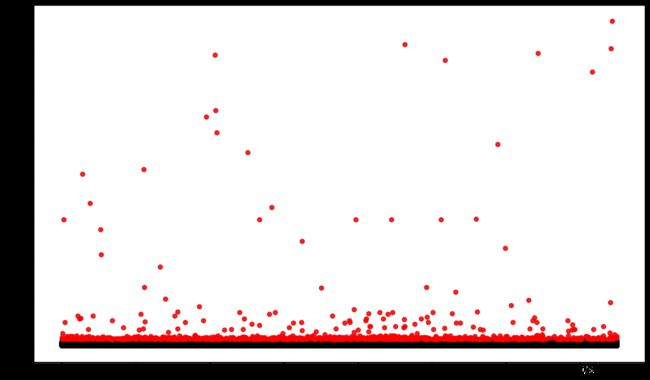
结果如下：

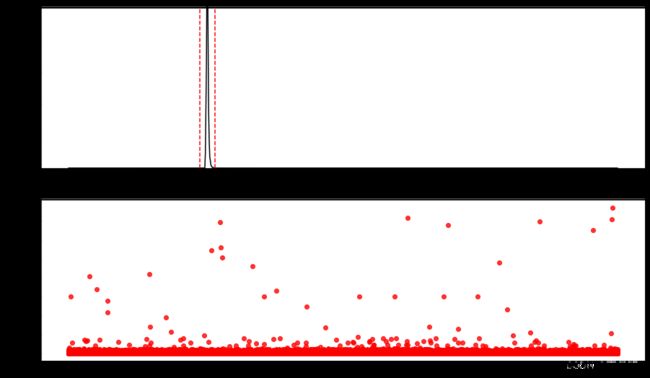
显然，这条路行不通，这样做的话所有的点都成了离群点了。

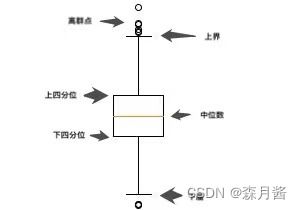
️根据箱线图分析

想要理解箱线图，首先我们需要理解箱线图的含义。

上四分位（Q1）：只有四分之一的值大于该四分位值
下四分位（Q3）：只有四分之一的值小于该四分位值
上界： Q1 + 1.5x（Q1-Q3）
下界： Q3 - 1.5 x（Q1-Q3）

超过上下界的点即被视为异常点，下面我们还是使用上述数据作为例子，首先绘制箱线图。

import seaborn as sns
plt.figure(figsize=(3,5), dpi=90)
sns.boxplot(y=train_data['power'], data=train_data)

由于异常点较多，导致原来的值都没有了，所以这里对异常点先做删除处理。

q1 = train_data['power'].quantile(0.75)
q3 = train_data['power'].quantile(0.25)
iqr = q1-q3
train_data.drop(train_data.loc[lambda x:x['power'] > q1 + 1.5 * iqr].index, inplace=True)
train_data.drop(train_data.loc[lambda x:x['power'] < q3 - 1.5 * iqr].index, inplace=True)

plt.figure(figsize=(3,5), dpi=90)
sns.boxplot(y=train_data['power'], data=train_data)

结果如下：

同样，这部分我也编写了相关函数:

def box(data, col,scale=1.5):
    # data: Dataframe数据
    # col：要处理的列名
    # scale: 默认为1.5
    # return: 高于设定的索引和低于设定的索引
    q1 = data[col].quantile(0.75)
    q3 = data[col].quantile(0.25)
    iqr = q1-q3
    high_power = train_data.loc[lambda x:x['power'] > q1 + scale * iqr].index
    low_power = train_data.loc[lambda x:x['power'] < q3 - scale * iqr].index
    return high_power,low_power
print(box(train_data, 'power'))

检测出的误差如下：

处理异常值

• 不处理：直接不对异常值进行处理，根据观察数据不同的异常情况使用此种方法。
• 删除数据：可以选择直接删除异常数据，但是前提是数据的异常值不能过高。
• 按照缺失值处理：可以按照处理缺失值的方法进行处理，根据不同的情况使用不同的方式。

总结

本次我们列举了比较常用的几种分析异常值的方法，要根据数据的不同使用不同的方法来处理。

本系列从数据处理到模型构建的全部文章已经更新完毕，感兴趣的同学可以点击下方链接支持一下。

• 【建议收藏】机器学习数据预处理（一）——缺失值处理方法（内附代码）
• 【建议收藏】机器学习数据预处理（二）——异常值处理方法（内附代码）
• 【建议收藏】机器学习数据预处理（三）——数据分桶及数据标准化（内附代码）
• 【建议收藏】机器学习数据预处理（四）——特征构造（内附代码）
• 【建议收藏】机器学习数据预处理（五）——特征选择（内附代码）
• 【建议收藏】机器学习模型构建（一）——建模调参（内附代码）
• 【建议收藏】机器学习模型构建（二）——模型融合（内附代码）