利用逻辑回归进行用户流失预测分析

1.项目背景

客户流失是所有与消费者挂钩行业都会关注的点。因为发展一个新客户是需要一定成本的，一旦客户流失，除了浪费拉新成本，还需要花费更多的用户召回成本。
所以，电信行业在竞争日益激烈当下，如何挽留更多用户成为一项关键业务指标。为了更好运营用户，这就要求要了解流失用户的特征，分析流失原因，预测用户流失，确定挽留目标用户并制定有效方案。

2.明确分析问题

1. 分析用户特征与流失的关系。
2. 从整体情况看，流失用户普遍具有哪些特征？
3. 尝试找到合适的模型预测流失用户。
4. 针对性给出增加用户黏性、预防流失的建议。

3.数据理解

本数据集来源Kaggle上公开的某电信公司的用户数据，共包含7043条数据，共21个字段。

4.数据清洗

数据清洗的“完全合一”规则：

• 完整性：单条数据是否存在空值，统计的字段是否完善。
• 全面性：观察某一列的全部数值，通过常识来判断该列是否有问题，比如：数据定义、单位标识、数据本身。
• 合法性：数据的类型、内容、大小的合法性。比如数据中是否存在非ASCII字符，性别存在了未知，年龄超过了150等。
• 唯一性：数据是否存在重复记录，因为数据通常来自不同渠道的汇总，重复的情况是常见的。行数据、列数据都需要是唯一的。

4.1数据导入

# 导入数据分析需要的包
import pandas as pd
import numpy as np
# 可视化包
import seaborn as sns
sns.set(style="whitegrid")
import matplotlib.pyplot as plt
%matplotlib inline
# 忽略警告信息
import warnings
warnings.filterwarnings('ignore')
# 显示中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
# 导入数据集
df=pd.read_csv('./WA_Fn-UseC_-Telco-Customer-Churn.csv')
# 查看数据
df.head(5)

4.2查看数据类型

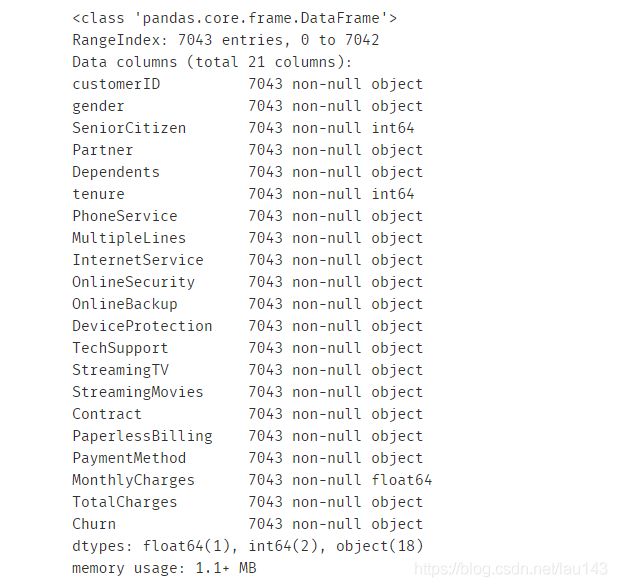
df.info()

MonthlyCharges和TotalCharges都为费用，类型都应该为数值,
但通过查看发现TotalCharges为object对象类型，需要转化数值类型。

#强制转换数字(包括字符串)
df['TotalCharges']=df['TotalCharges'].apply(pd.to_numeric,errors='coerce')
#df['TotalCharges'] = df['TotalCharges'].convert_objects(convert_numeric=True)
df['TotalCharges'].dtypes
# 输出结果
dtype('float64')

# convert_numeric=True 表示强制转换数字（包括字符串），不可转换的值Nan
df['MonthlyCharges']=df['MonthlyCharges'].convert_objects(convert_numeric=True)                                                     
df['MonthlyCharges'].dtypes
# 输出结果
dtype('float64')

4.3缺失值处理

# 查看缺失值
df.isnull().sum()

# 定位缺失值所在行，查看具体情况
df[df['TotalCharges']!=df['TotalCharges']][['tenure','MonthlyCharges','TotalCharges']]

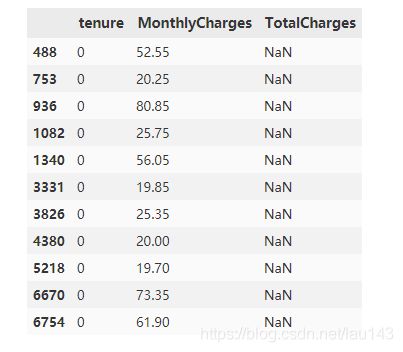
分析：
发现这11个用户tenure（入网时常）为0，推测是当月新入网用户。
根据一般经验，用户即使在注册的当月流失，也需缴纳当月费用。
因此将这11个用户入网时长改为1，将总消费额填充为月消费额，符合实际情况。

• 将总消费额填充为月消费额

#将总消费额填充为月消费额
df.loc[:,'TotalCharges'].replace(np.nan,df.loc[:,'MonthlyCharges'],inplace=True)
#查看是否替换成功
df[df['tenure']==0][['tenure','MonthlyCharges','TotalCharges']]

• 将‘tenure’入网时长从0修改为1

# 将‘tenure’入网时长从0修改为1
df.loc[:,'tenure'].replace(to_replace=0,value=1,inplace=True)

4.4数据归一化处理

对Churn 列中的值 Yes和 No分别用 1和 0替换，方便后续处理

df['Churn'].replace( 'Yes', 1,inplace = True)
df['Churn'].replace( 'No',  0,inplace = True)
df['Churn'].head()

# 保存数据集
df.to_csv('./Telecom_customer churn1.csv')

5.流失用户特征分析

根据用户主要特征。将用户属性分为三类，用户属性、服务属性及合同属性。

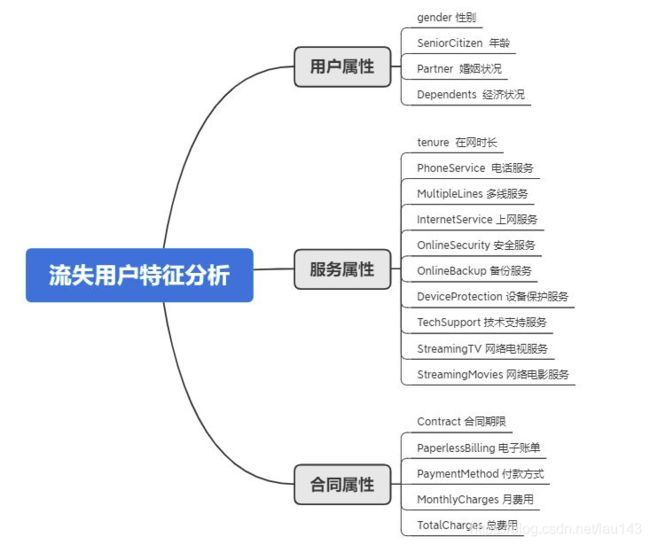
• 查看客户总体流失情况

# 查看总体客户流失情况
churnvalue = df["Churn"].value_counts()
labels = df["Churn"].value_counts().index
plt.pie(churnvalue,
        labels=["未流失","流失"],
        explode=(0.1,0),
        autopct='%.2f%%', 
        shadow=True,)
plt.title("客户流失率比例",size=24)
plt.show()

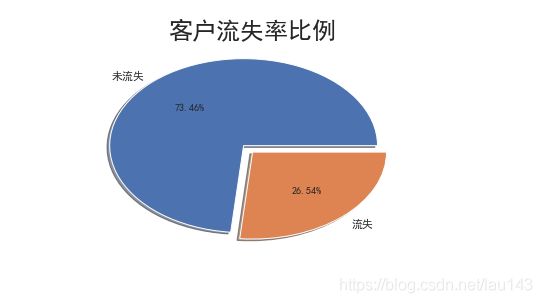
分析：
从饼形图中看出，流失客户占总客户数的四分之一比例，流失率达26.54%

5.1用户属性分析

fig, axes = plt.subplots(2, 2, figsize=(12,12))
plt.subplot(2,2,1) 
# palette参数表示设置颜色
gender=sns.countplot(x='gender',hue="Churn",data=df,palette="Pastel2") 
plt.xlabel("性别",fontsize=16)
plt.ylabel('count',fontsize=16)
plt.tick_params(labelsize=12)     # 设置坐标轴字体大小
plt.title("Churn by Gender",fontsize=18)

plt.subplot(2,2,2)
seniorcitizen=sns.countplot(x="SeniorCitizen",hue="Churn",data=df,palette="Pastel2")
plt.xlabel("年龄（0代表是年轻人，1代表是老年人）")
plt.title("Churn by Senior Citizen",fontsize=18)
plt.ylabel('count',fontsize=16)
plt.tick_params(labelsize=12)   # 设置坐标轴字体大小

plt.subplot(2,2,3)
partner=sns.countplot(x="Partner",hue="Churn",data=df,palette="Pastel2")
plt.xlabel("婚姻状态（yes代表已婚，no代表未婚）")
plt.title("Churn by Partner",fontsize=18)
plt.ylabel('count',fontsize=16)
plt.tick_params(labelsize=12)   # 设置坐标轴字体大小

plt.subplot(2,2,4)
dependents=sns.countplot(x="Dependents",hue="Churn",data=df,palette="Pastel2")
plt.xlabel("经济能力（yes代表经济独立，no代表未独立）")
plt.title("Churn by Dependents",fontsize=18)
plt.ylabel('count',fontsize=16)
plt.tick_params(labelsize=12)   # 设置坐标轴字体大小
plt.tight_layout()
plt.show()

分析：

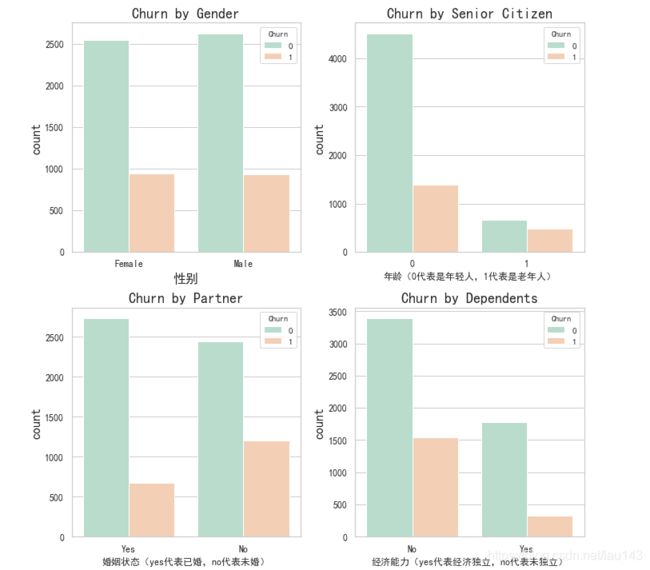
• 用户流失与性别基本无关，差异性较小；

• 年老客户用户量相对较少，但流失率较高；

• 未婚用户流失率高于已婚用户；

• 经济能力未独立的用户流失率高于经济能力独立用户

5.2服务属性

查看网络安全服务、在线备份业务、设备保护业务、技术支持服务、
网络电视、网络电影和无互联网服务对客户流失率的影响。

covariables=["OnlineSecurity", "OnlineBackup", "DeviceProtection", "TechSupport", "StreamingTV", "StreamingMovies"]
fig,axes=plt.subplots(2,3,figsize=(20,12))
for i, item in enumerate(covariables):
    '''
    0,'OnlineSecurit'
    1,'OnlineBackup'
    '''
    plt.subplot(2,3,(i+1))
    ax=sns.countplot(x=item,hue="Churn",data=df,palette="Set2",order=["Yes","No","No internet service"])
    plt.xlabel(str(item),fontsize=16)
    plt.tick_params(labelsize=14)     # 设置坐标轴字体大小
    plt.title("Churn by "+ str(item),fontsize=20)
    i=i+1
plt.tight_layout()
plt.show()

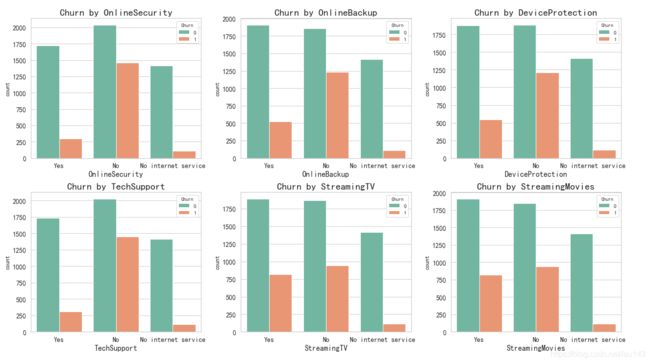
分析：
在这六个服务属性中，开通相关服务的用户流失率较低，
说明有这些方面需求的客户对此服务还比较满意，客户群体也比较稳定。
No internetserive这部分客户群体流失率基本相同，且相对较低。

5.3合同属性

• 查看合同签订方式对用户流失的影响

fig = plt.figure(figsize=(12,8))
sns.barplot(x="Contract",
            y="Churn", 
            data=df, 
            palette="Pastel1", 
            order= ['Month-to-month', 
                    'One year', 'Two year'])
plt.title("Churn by Contract type",fontsize=20)
plt.xlabel('Contract',fontsize=16)
plt.ylabel('Churn',fontsize=16)
plt.tick_params(labelsize=13)     # 设置坐标轴字体大小
plt.show()

分析：
从柱状图中看出，合同期限越长，流失率越低，一部分原因是选择长期合同的客户原本就比较稳定，
另外一个原因是长期合同具有长期约束率，在客户签订合同时，可以针对一次签订长期合同的客户进行优惠促销。

• 查看付款方式对用户流失率的影响

plt.figure(figsize=(12,8))
sns.barplot(x="PaymentMethod",y="Churn", data=df, palette="Pastel1", order= ['Bank transfer (automatic)', 'Credit card (automatic)', 'Electronic check','Mailed check'])
plt.title("Churn by PaymentMethod type",fontsize=20)
plt.xlabel('PaymentMethod',fontsize=16)
plt.ylabel('Churn',fontsize=16)
plt.tick_params(labelsize=13)     # 设置坐标轴字体大小
plt.show()

分析：
在四种支付方式中，使用Electronic check的用户流失率最高，其他三种支付方式基本持平，因此可以推断电子账单在设计上影响用户体验。

• 查看正常用户与流失用户在月消费金额上的差别

plt.figure(figsize=(10,6))
g = sns.FacetGrid(data = df,hue = 'Churn', height=4, aspect=3)
g.map(sns.distplot,'MonthlyCharges',norm_hist=True)
g.add_legend()
plt.ylabel('density',fontsize=16)
plt.xlabel('MonthlyCharges',fontsize=16)
plt.tick_params(labelsize=13)     # 设置坐标轴字体大小
plt.tight_layout()
plt.show()

分析：
从上图看出，月消费额大约在70-110这个区间内的用户流失率相对较高。

• 查看正常用户与流失用户在总消费金额上的差别

g = sns.FacetGrid(data = df,hue = 'Churn', height=4, aspect=3)
g.map(sns.distplot,'TotalCharges',norm_hist=True)
g.add_legend()
plt.ylabel('density',fontsize=16)
plt.xlabel('TotalCharges',fontsize=16)
plt.tick_params(labelsize=13)     # 设置坐标轴字体大小
plt.show()

分析：
从上图看出，总消费金额越多，客户流失率会相对较低,
说明当客户对此产品形成一定消费习惯后，忠诚度会升高。

6.用户流失预测

对数据集进一步清洗和提取特征，通过特征选取对数据进行降维，采用机器学习模型应用于测试数据集，
然后对构建的分类模型准确性进行分析。

7 数据预处理

#导入数据分析需要的包
import pandas as pd
import numpy as np
#可视化包
import seaborn as sns
sns.set(style="whitegrid")
import matplotlib.pyplot as plt
%matplotlib inline
#忽略警告信息
import warnings
warnings.filterwarnings('ignore')
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
#导入数据集
df = pd.read_csv('./Telecom_customer churn1.csv')

# CustomerID表示每个客户的标识，对后续建模不影响，这里选择删除CustomerID列
customerID=df['customerID']
df.drop("customerID",axis=1, inplace=True)
df.drop('Unnamed: 0',axis=1,inplace=True)
df.head() 

7.1 特征编码

特征主要分为连续特征和离散特征，其中离散特征根据特征之间是否有大小关系又细分为两类。

• 连续特征：“tenure”、“MonthlyCharges”、“TotalCharges”，一般采用归一标准化方式处理。
• 离散特征：特征之间没有大小关系，如：PaymentMethod：[bank transfer，credit card，electronic check，mailed check]，付费方式之间没有大小关系，一般采用one-hot编码。
• 离散特征：特征之间有大小关联，则采用数值映射。本数据集无此类特征。

7.1.1 连续特征编码

对tenure（在网时长），MonthlyCharges（月费用），TotalCharges（总费用）三个连续特征进行标准化处理，
使特征数据标准为1，均值为0，符合标准的正态分布，降低数值特征过大对预测结果的影响。

from sklearn.preprocessing import StandardScaler  
# 实例化一个转换器类
scaler = StandardScaler(copy=False)
# 调用fit_transform，其作用是先拟合数据，然后转化它将其转化为标准形式
scaler.fit_transform(df[['tenure','MonthlyCharges','TotalCharges']])
#利用transform函数实现标准化，作用是通过找中心和缩放等实现标准化
df[['tenure','MonthlyCharges','TotalCharges']]=scaler.transform(df[['tenure','MonthlyCharges','TotalCharges']])
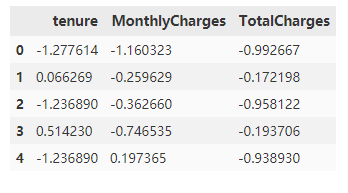
df[['tenure','MonthlyCharges','TotalCharges']].head()

7.1.2 离散特征编码

# 查看对象类型字段中存在的值
def uni(columnlabel):
    # unique函数去除其中重复的元素，返回唯一值
    print(columnlabel,"--" ,df[columnlabel].unique())
    
dfobject=df.select_dtypes(['object'])
for i in range(0,len(dfobject.columns)):
    uni(dfobject.columns[i])

结合服务属性，发现No internet service（无互联网服务）对客户流失率影响很小，
这些客户不使用任何互联网产品，因此可以将No internet service 和 No 是一样的效果，
可以使用 No 替代 No internet service

df.replace(to_replace='No internet service', value='No', inplace=True)
df.replace(to_replace='No phone service', value='No', inplace=True)
#再次查看
for i in range(0,len(dfobject.columns)):
    uni(dfobject.columns[i])

7.1.3 使用Scikit-learn标签编码，将离散特征转换为整数编码

# 编码转换
from sklearn.preprocessing import LabelEncoder  
def labelencode(columnlabel):
    df[columnlabel] = LabelEncoder().fit_transform(df[columnlabel])
    
for i in range(0,len(dfobject.columns)):
    labelencode(dfobject.columns[i])
    
for i in range(0,len(dfobject.columns)):
    uni(dfobject.columns[i])

7.2 数据相关性分析

电信用户是否流失与各变量之间的相关性

plt.figure(figsize=(16,8))
df.corr()['Churn'].sort_values(ascending = False).plot(kind='bar')
plt.tick_params(labelsize=14)     # 设置坐标轴字体大小
plt.xticks(rotation=45)         # 设置x轴文字转向
plt.title("Correlations between Churn and variables",fontsize=20)
plt.show()

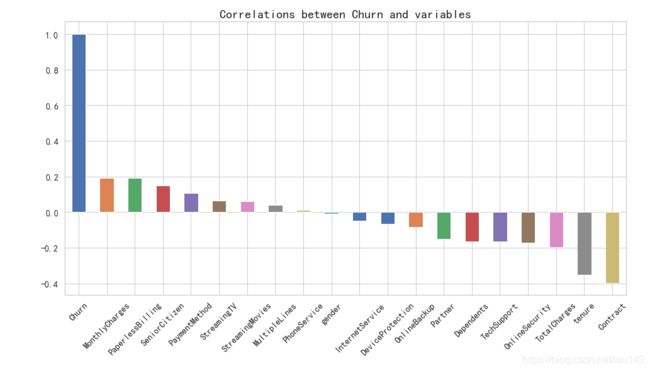
分析：
从上图可以直观看出，PhoneService 、gender这两个变量与churn目标变量相关性最弱。

7.3 特征选取

特征值选取时，去除相关性较弱的PhoneService 、gender两个变量。这里目标变量是churn。

# 特征选取
dropFea = ['gender','PhoneService']
df.drop(dropFea, inplace=True, axis =1)
# 深拷贝
X=df.copy()
X.drop(['Churn'],axis=1, inplace=True)
y=df["Churn"]
#查看预处理后的数据
X.head()

8 构建模型

8.1 样本不均衡处理

# 正常用户和流失用户数量分布
count_Churn = pd.value_counts(df['Churn']).sort_index()
plt.figure(figsize=(8,6))
count_Churn.plot(kind = 'bar')
plt.title("Churn histogram",size=20)
plt.xlabel("Churn")
plt.ylabel("Frequency")

从图中看出，该样本中正常用户和流失用户数量分布不平衡，建模过程中容易忽略数量较少的流失客户，模型出现一边倒的情况，如果模型不重视异常数据，就有悖我们建模的初衷，常用的解决方案有下采样和上采样，我们这里利用下采样方案进行处理。

下采样，简单的理解就是，两个唯一值，以数量最少值的个数为标准，随机对另外一个值选取相同个数，从而满足样本均衡化。本案例流失客户数为1869，从正常交易数据中同样选取1869个，各占比50%，总共3738个。

#下采样方案实现过程

#计算 Churn=1的样本的数量
number_records_Churn = len(df[df.Churn == 1]) 
# 取出Churn=1的样本对应的行索引
Churn_indices = np.array(df[df.Churn == 1].index) 
# 取出Churn=0样本对应的行索引
normal_indices = df[df.Churn == 0].index  

random_normal_indices = np.random.choice(normal_indices, number_records_Churn, replace = False) #随机选择和number_records_Churn一致的正常用户样本量
random_normal_indices = np.array(random_normal_indices) #转换成numpy的格式       

under_sample_indices = np.concatenate([Churn_indices,random_normal_indices])  #将正负样本拼接在一起

#下采样数据集
under_sample_data = df.iloc[under_sample_indices,:]

X_undersample = under_sample_data.iloc[:, under_sample_data.columns != 'Churn']  #下采样数据集的数据，可以理解为自变量
y_undersample = under_sample_data.iloc[:, under_sample_data.columns == 'Churn']  #下采样数据集的lable，可以理解为因变量

# 查看正负各自占比
print("Percentage of Churn_no: ", len(under_sample_data[under_sample_data.Churn == 0])/len(under_sample_data))
print("Percentage of Churn_yes: ", len(under_sample_data[under_sample_data.Churn == 1])/len(under_sample_data))
#查看总数
print("Total number of Churn in resampled data: ", len(under_sample_data))

'''
Percentage of Churn_no:  0.5
Percentage of Churn_yes:  0.5
Total number of Churn in resampled data:  3738
'''

8.2 模型交叉验证

将数据集分为训练集和测试集，以帮助完成模型测试工作

# 将数据集分成训练集和测试集，比例为7:3
from sklearn.linear_model import LogisticRegression          # 逻辑回归
from sklearn.metrics import precision_score, recall_score, f1_score,accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import GridSearchCV  # 网格搜索
# 把整体数据集进行切分
# test_size = 0.3, 表示30%的数据作为测试集合，
# 剩余70%的数据作为训练集；state=0在切分时进行数据重洗牌的标识位。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state = 40)
print("原始训练集包含样本数量: ", len(X_train))
print("原始测试集包含样本数量:  ", len(X_test))
print("原始样本总数: ", len(X_train)+len(X_test))

'''
原始训练集包含样本数量:  4930
原始测试集包含样本数量:   2113
原始样本总数:  7043

下采样训练集包含样本数量:  2616
下采样测试集包含样本数量:   1122
下采样样本总数: 3738
'''

8.3 逻辑回归建模

# 逻辑回归建模
model = LogisticRegression(solver='liblinear', penalty='l1')
model.fit(X_train, y_train)

# 用建好的模型model在测试集进行验证
predictions = model.predict(X_test)
actual_score = accuracy_score(y_test, predictions)
print(actual_score)
'''
0.7846663511594889
'''

8.2.1 正则化惩罚

在机器学习任务中经常会遇到过拟合现象，最常见的情况就是随着模型复杂程度的提升，训练集效果越来越好，但是测试集效果反而越来越差。如果在训练集上得到的参数值忽高忽低，很可能导致过拟合，这时候就需要用到正则化惩罚，即惩罚数值较大的权重参数，降低它们对结果的影响。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,precision_recall_curve,auc,roc_auc_score,roc_curve,recall_score,classification_report

#Recall = TP/(TP+FN)
from sklearn.linear_model import LogisticRegression
# from sklearn.cross_validation import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report
from sklearn.model_selection import cross_val_predict, KFold, cross_val_score

#print(help(KFold))

def printing_Kfold_scores(x_train_data,y_train_data):
    #fold = KFold(len(y_train_data),5,shuffle=False)
    fold = KFold(5,shuffle=False)

    # 定义不同力度的正则化惩罚力度
    c_param_range = [0.01,0.1,1,10,100]
    # 展示结果用的表格
    results_table = pd.DataFrame(index = range(len(c_param_range),2), columns = ['C_parameter','Mean recall score'])
    results_table['C_parameter'] = c_param_range

    # k-fold 表示K折的交叉验证，这里会得到两个索引集合: 训练集 = indices[0], 验证集 = indices[1]
    j = 0
    #循环遍历不同的参数
    for c_param in c_param_range:
        print('-------------------------------------------')
        print('正则化惩罚力度: ', c_param)
        print('-------------------------------------------')
        print('')

        recall_accs = []

        #下面来分解执行交叉验证
        #for iteration, indices in enumerate(fold,start=1):
        for iteration, indices in enumerate(fold.split(x_train_data)):

            # 指定算法模型，并且给定参数
            #lr = LogisticRegression(C = c_param, penalty = 'l1')
            lr = LogisticRegression(C = c_param, penalty = 'l1',solver='liblinear')

            # 训练模型，注意索引不要给错，训练的时候一定传入的是训练集，所以X和Y的索引都是0
            lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())

            # 建立好模型后，预测模型结果，这里用的就是验证集，索引为1
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)

            # 有了预测结果之后就可以来进行评估了，这里recall_score需要传入预测值和真实值。
            recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
            
            recall_accs.append(recall_acc)
            print('Iteration ', iteration,': 召回率 = ', recall_acc)


        # 当执行完所有的交叉验证后，计算平均结果
        results_table.loc[j,'Mean recall score'] = np.mean(recall_accs)
        j += 1
        print('')
        print('平均召回率 ', np.mean(recall_accs))
        print('')

    #找到最好的参数，Recall越高，效果越好
    best_c = results_table.loc[results_table['Mean recall score'].astype('float32').idxmax()]['C_parameter']

    # 打印最好的结果
    print('*********************************************************************************')
    print('效果最好的模型所选参数 = ', best_c)
    print('*********************************************************************************')

    return best_c

#交叉验证与不同参数结果
best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample) 

8.2.2 混淆矩阵

上面已经训练好模型，这里利用混淆矩阵进行可视化展示分析。

# 定义混淆矩阵的画法
 def plot_confusion_matrix(cm, classes,
                              title='Confusion matrix',
                              cmap=plt.cm.Blues):
        """
        绘制混淆矩阵
        """
        plt.imshow(cm, interpolation='nearest', cmap=cmap)
        plt.title(title)
        plt.colorbar()
        tick_marks = np.arange(len(classes))
        plt.xticks(tick_marks, classes, rotation=0)
        plt.yticks(tick_marks, classes)

        thresh = cm.max() / 2.
        for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
            plt.text(j, i, cm[i, j],
                     horizontalalignment="center",
                     color="white" if cm[i, j] > thresh else "black")

        plt.tight_layout()
        plt.ylabel('True label')
        plt.xlabel('Predicted label')

传入实际预测结果，调用之前的逻辑回归模型，得到测试结果，再把数据的真实标签值传进去即可：

import itertools
# lr = LogisticRegression(C = best_c, penalty = 'l1')
lr = LogisticRegression(C = best_c, penalty = 'l1', solver='liblinear')
lr.fit(X_train,y_train.values.ravel())
y_pred = lr.predict(X_test.values)

# 计算所需值
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)

print("召回率: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# 绘制
class_names = [0,1]
plt.figure(figsize=(10,8))
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()

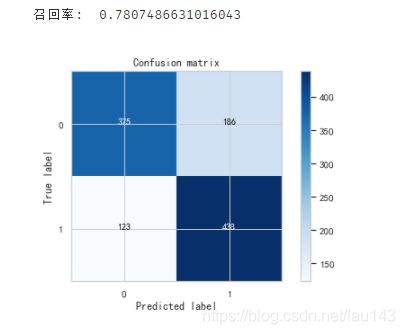
真实为1的召回率：表示在流失客户中有多少能预测到，覆盖面的大小。

用公式表达即：
Recall=TN/(TN+FP)=438/(438+123)=0.78

召回率为 0.78，该分数还算理想。因为下采样时对原数据进行过处理，
模型最终要回归实际，这里需要在整体数据集的测试集进行评估效果，使模型更加可信

lr = LogisticRegression(C = best_c, penalty = 'l1', solver='liblinear')
lr.fit(X_train,y_train.values.ravel())
y_pred = lr.predict(X_test.values)

# 计算所需值
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("召回率: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# 绘制
class_names = [0,1]
plt.figure(figsize=(10,8))
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()

在原始数据进行测试，得到的召回率为0.79，两者结果比较接近。

8.2.3 调整阈值

对于逻辑回归算法来说，我们还可以指定一个阈值，也就是说最终结果的概率是大于多少我们把它当成是正或者负样本。这里通过Sigmoid函数将得分值转换成概率值，默认情况下，模型都是以0.5为界限来划分类别：p>0.5为正例，p<0.5为负例。0.5是一个经验值，可以根据实际经验进行调整。我们指定0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9，9个不同阈值，分别查看模型效果。

# 用之前最好的参数来进行建模
# lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr = LogisticRegression(C = 0.01, penalty = 'l1',solver='liblinear')

# 训练模型，还是用下采样的数据集
lr.fit(X_train_undersample,y_train_undersample.values.ravel())

# 得到预测结果的概率值
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)

#指定不同的阈值
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]

plt.figure(figsize=(10,10))

j = 1

# 用混淆矩阵来进行展示
for i in thresholds:
    y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i

    plt.subplot(3,3,j)
    j += 1

    cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
    np.set_printoptions(precision=2)

    print("给定阈值为:",i,"时测试集召回率: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

    class_names = [0,1]
    plot_confusion_matrix(cnf_matrix
                          , classes=class_names
                          , title='Threshold >= %s'%i)

'''
给定阈值为: 0.1 时测试集召回率:  0.9982174688057041
给定阈值为: 0.2 时测试集召回率:  0.9732620320855615
给定阈值为: 0.3 时测试集召回率:  0.9411764705882353
给定阈值为: 0.4 时测试集召回率:  0.8841354723707665
给定阈值为: 0.5 时测试集召回率:  0.7807486631016043
给定阈值为: 0.6 时测试集召回率:  0.6042780748663101
给定阈值为: 0.7 时测试集召回率:  0.36185383244206776
给定阈值为: 0.8 时测试集召回率:  0.0071301247771836
给定阈值为: 0.9 时测试集召回率:  0.0
'''

通过对比九个不同阈值发现，当阈值越小时，召回率越高，但“误杀率”也比较高，实际意思不大。随着阈值增大，召回率降低，也就是“漏检”的数量增多，但“误杀率”也会降低。

如当阈值等于0.9时，有560个流失客户被正确预测，有1个流失客户没有被预测到，但有510个正常用户被误认为是流失用户，召回率为0.99，但精确率只有0.54；当阈值等于0.5时，有439个流失客户被正确预测，有122个流失客户没有被预测到，有170个正常用户被误认为是流失用户，召回率为0.78，准确率为0.73，准确率有所上升。

在预测客户流失中，理想状态时，所有的流失用户都被预测到(召回率)，这样我们就可以提前对这部分客户进行精细化运营，有效阻止客户流失，提高客户留存率；同时，也不存在正常用户被误判断为流失用户，减少运营成本，提高用户体验。但两者很难兼得，具体阈值调整需要结合实际业务，从实际业务出发，选择最优阈值。

9 建模

9.1 数据处理

9.1.1连续特征离散化

为了使模型更加稳定，使预测效果更好，对数值类型（tenure、MonthlyCharges）进行分析分箱操作。
其方法分为有监督分箱（卡方分箱、最小熵法分箱）和无监督分箱（等频分箱、等距分箱）。这里采用无监督分箱中的等频分箱进行操作。

df['tenure']=pd.qcut(df['tenure'],5)
df['MonthlyCharges']=pd.qcut(df['MonthlyCharges'],5)

9.1.2 One-Hot编码

前面，我们对区分度比较大的特征进行再次处理，如：Contract、InternetService、PaymentMethod等，同时这些变量为离散数据且数据内容标称属性，其数据本身不具有任何顺序意思。前面统一采用LabelEncode标签编码的方式欠妥。这里我们修正利用One-Hot独立编码的方式，构造虚拟变量。

sub_df=df.loc[:,['Contract','InternetService','PaymentMethod']] 
df = df.join(pd.get_dummies(sub_df))  #编码后并入数据集

9.2 模型调参 ——GridSearchCV（网格搜索）

GridSearchCV可以保证在指定的参数范围内自动找到精度最优的参数，但这也是网格搜索的缺陷所在，
它要求遍历所有可能参数的组合，在面对大数据集和多参数的情况下，非常耗时，适用范围有限。

本数据集体量较小，且决策树涉及参数较少，我们选择其中三个特征：criterion、max_depth和min_samples_split。

criterion：特征选择标准,可以使用"gini"或者"entropy"，前者代表基尼系数，后者代表信息增益。

max_depth：决策树最大深度。

min_samples_split：部节点再划分所需最小样本数。

#调用scikit-learn中集成的决策树tree
from sklearn import tree
#模型调参利器 gridSearchCV（网格搜索）
from sklearn.model_selection import GridSearchCV  
from sklearn import metrics
param_grid = {
    'criterion' : ['entropy','gini'], #特征选择标准
    'max_depth' : [2,3,4,5,6,7,8,9,10],            #决策树最大深度
    'min_samples_split' : [4,8,12,16,20,24,28]    #内部节点再划分所需最小样本数
}
clf = tree.DecisionTreeClassifier()
clfcv = GridSearchCV(estimator=clf,param_grid=param_grid,scoring='roc_auc',cv=4)
clfcv.fit(X_train,y_train)
clfcv.best_params_   #best_params_ ：最佳模型参数

'''
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_split': 8}
'''

9.3 构建决策树

利用最佳模型参数进行建树
决策树由结点和有向边组成。结点有两种类型：内部结点和叶结点，其中内部结点表示一个特征或属性，叶结点表示一个类。一般的，一棵决策树包含一个根结点、若干个内部结点和若干个叶结点。叶结点对应于决策结果，其他每个结点则对应于一个属性测试。

#利用balanced解决样本不均衡问题
clf= tree.DecisionTreeClassifier(criterion='entropy',
                                 max_depth=5,
                                 min_samples_split=4,
                                 class_weight="balanced")
clf.fit(X_train,y_train)
train_est = clf.predict(X_train)  #  用模型预测训练集的结果
train_est_p=clf.predict_proba(X_train)[:,1]  #用模型预测训练集的概率
test_est=clf.predict(X_test)  #  用模型预测测试集的结果
test_est_p=clf.predict_proba(X_test)[:,1]  #  用模型预测测试集的概率
from sklearn.metrics import accuracy_score
accuracy_score(y_test, clf.predict(X_test))

'''
0.7326076668244202
'''

ROC曲线中的表现

fpr_test, tpr_test, th_test = metrics.roc_curve(y_test, test_est_p)
fpr_train, tpr_train, th_train = metrics.roc_curve(y_train, train_est_p)
plt.figure(figsize=[6,6])
plt.plot(fpr_test, tpr_test, color='blue')
plt.plot(fpr_train, tpr_train, color='red')
plt.title('ROC curve')
plt.show()

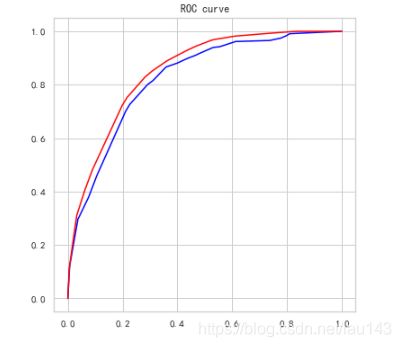
从ROC曲线可以观察到训练数据和测试数据曲线重合度较高，拟合较好。

模型已经构建好，决策树有独特之处，就是可以展示决策过程。

#调用scikit-learn中集成的决策树tree
from sklearn import tree
clf = tree.DecisionTreeClassifier(max_depth=5) 
clf = clf.fit(X_train, y_train)

#展示决策树，定义函数
with open("No-Yes.dot", 'w') as f:
     f = tree.export_graphviz(clf,
                              out_file=f,
                              max_depth = 5,   #最优5层
                              impurity = True,
                              feature_names = list(X_train),
                              class_names = ["Churn_No", "Churn_Yes"],
                              rounded = True,
                              filled= True )

from subprocess import check_call
check_call(['C:/Program Files/Graphviz 2.44.1/bin/dot','-Tpng','No-Yes.dot','-o','No-Yes.png'])

from IPython.display import Image as PImage
from PIL import Image, ImageDraw, ImageFont
img = Image.open("No-Yes.png")
draw = ImageDraw.Draw(img)
img.save('output.png')
PImage("output.png")

这颗树从InternetService_Fiber optic这一分类特征的用户群体发展而来。可以明显发现，在网时长在0到6个月之间的年轻人群体很容易流失，但0到6个月之间中用Credit card (automatic)这种付款方式的群体则不容易流失；合同为Month-to-month形式的客户容易流失，但其中月缴费金额在(25.05, 58.83]之间的用户则比较稳定、不容易流失。

基于上述分析，给出运营建议：

• 新入网用户比较容易流失，尤其年轻用户群体，应当针对年轻人细化运营策略；
• 对比分析Credit card (automatic)该支付方式相对其他三类付款方式的优点，分析其独特成功之处，用来改善其他付款方式的服务，或者可以在支付时利用优惠减免方式让客户直接选择该支付方式；
• 月缴费额和开通服务功能直接相关，相对于没有开通服务的用户，开通享受多种附加增值服务的用户相对稳定，可以在客户签订时赠送用户体验资格，让更多的用户了解增值服务的好处，促使开通相关服务，从而提高客户留存度。

前面，我们只是单独知道Month-to-month、Fiber optic、在网时间短等这部分群体容易流失，具体相互之间决策关系并不清楚，我们可以通过决策树更加直观的挖掘相互关系，实现策略联动，这也是决策树可视化的独特好处。

10 结论和建议

流失用户特征：

• 用户属性：老年用户，未婚用户、经济未独立的用户更容易流失；

• 服务属性：未开通相关附加增值服务的用户更容易流失；

• 合同属性：签订的合同期较短，电子账单支付、月租费约70-110元的客户容易流失。

建议：

• 新入网用户比较容易流失，尤其年轻用户群体，应当针对年轻人细化运营策略；
• 对比分析Credit card (automatic)该支付方式相对其他三类付款方式的优点，分析其独特成功之处，用来改善其他付款方式的服务，或者可以在支付时利用优惠减免方式让客户直接选择该支付方式；
• 月缴费额和开通服务功能直接相关，相对于没有开通服务的用户，开通享受多种附加增值服务的用户相对稳定，可以在客户签订时赠送用户体验资格，让更多的用户了解增值服务的好处，促使开通相关服务，从而提高客户留存度。