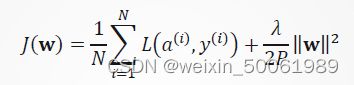Multilayer perceptron&Optimization algorithm

多层感知机和优化算法

目录

前言

一、Multilayer perceptron

二、BP算法

 三、BP算法的优缺点

四、Optimization algorithm

1、Momentum method

2、Adaptive Gradient

3、RMSProp: Root Mean Square Prop

4、Adam算法

总结

---

前言

        多层感知机是深度学习的基础，为了训练模型中，使得损失函数更好地接近最小值，对于小批量随机梯度下降提出了更好的优化算法，但是深度学习的目标是减少泛化误差。为了实现后者，除使优化算法来减少训练误差之外，我们还需要注意过拟合。

---

一、Multilayer perceptron

        传统机器学习的方法无法解决非线性问题，比如XOR问题，就是一个典型的线性不可分问题，如图无法用一条线解决分类问题。 

XOR

XOR图示

         可以使用多层感知机解决这个问题，在输入和输出层加一或多层隐单元，构成多层感知器(多层前馈神经网络)。加一层隐节点(单元)为三层网络，可解决XOR问题，如图所示。

多层感知机解决XOR问题

XOR问题表达式

        从这样一个简单的问题就能看出Multilayer perception的强大，可以解决非线性问题。实际上三层感知器可识别任一凸多边形或无界的凸区域。更多层感知器网络，可识别更为复杂的图形。这里给出两个定理，说明Multilayer perception的强大之处。

定理1　若隐层节点（单元）可任意设置，用三层阈值节点的网络，可以实现任意的二值逻辑函数。
定理2　若隐层节点（单元）可任意设置，用三层S型非线性特性节点的网络，可以一致逼近紧集上的连续函数或按 范数逼近紧集上的平方可积函数。

        这两个定理主要意义在于说明Multilayer perception可以描述任意函数，只用一层隐单元就能描述任意函数，但是实际操作上仅用一层是存在困难的，可能很难训练系统。

---

二、BP算法

        深度学习有一个损失函数作为目标函数，需要通过使这个目标函数(均方误差或者交叉熵损失)最小来更新权重。反向传播(BP)学习算法，即是梯度下降法在Multilayer perception的运用。很多问题没有解析解，所以使用梯度下降这一基本方法来求最小值。

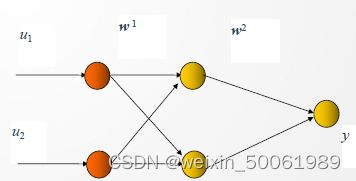
        Multilayer perception的结构：

Multilayer perception结构

        见图，u、y是网络的输入、输出向量，神经元用节点表示，网络由输入层、隐层和输出层节点组成，隐层可一层，也可多层(图中是单隐层)，前层至后层节点通过权联接。由于用BP学习算法，所以常称BP神经网络 。

① 正向传播是输入信号从输入层经隐层，传向输出层，若输出层得到了期望的输出，则学习算法结束；否则，转至反向传播。
② 反向传播是将误差(样本输出与网络输出之差）按原联接通路反向计算，由梯度下降法调整各层节点的权值和阈值，使误差减小。

        网络训练的目的，是使对每一个输入样本，调整网络参数，使输出均方误差最小化。

        考虑迭代算法，设初始权值为, k时刻权值为, 则使用泰勒级数展开，有：

         可以选择

        这样就能使得损失函数逐渐减小。

        BP算法基本思想：

        ① 设置初始权系数为较小的随机非零值；
        ② 给定输入/输出样本对，计算网络输出, 完成前向传播
        ③ 计算目标函数J。如J < , 训练成功，退出；否则转入④
        ④ 反向传播计算 由输出层，按梯度下降法将误差反向传播，逐层调整权值。

        至于算法具体推导的过程，可以参考具体的过程，实际上也很简单，就是一个求梯度的梯度的过程，也就是求偏导的过程，利用损失函数的梯度更新权重，来实现反向传播。如果有多个隐单元，可以看出从输出到输入逐层更新权重时，有一部分在计算过程中是相同的，也就是误差，实际上是对误差进行反传。实际上程序中对于梯度下降的计算，更多的依靠图论，这样可以大大减少多余的步骤。

        可以利用深度学习框架，来实现Multilayer perception，这里参考《动手学深度学习》给出简洁实现：

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
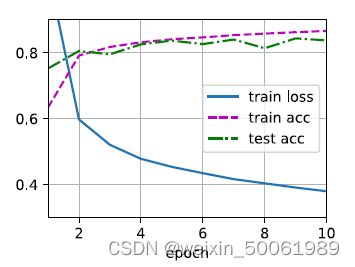
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

        使用的数据集为：Fashion-MNIST。结果：

结果

d2l.predict_ch3(net, test_iter) # 在一些测试集上使用

结果

 三、BP算法的优缺点

        为防止训练过程中权重过大，可以在这样一个最优化问题中的目标函数加上一个正则项，比如：

加入正则项的目标函数

         优点：

        学习完全自主；可逼近任意非线性函数。

        缺点：

        算法非全局收敛；收敛速度慢；学习速率α选择；神经网络如何设计(几层？节点数？)

        实际上对这些问题的研究促进了深度学习的发展，寻找问题，解决问题，促进发展。

---

四、Optimization algorithm

        这里仅关注优化算法的在最小化目标函数的性能，而不是模型的泛化误差，实际上目标函数取最小值时，并不一定使得整个模型的泛化误差最小。在深度学习中，⼤多数⽬标函数都很复杂，没有解析解。必须使⽤数值优化算法。

        深度学习存在很多挑战，比如：局部最小值、鞍点和梯度消失。

        局部最小值如图所示，并不是全局最小值：

局部最小值

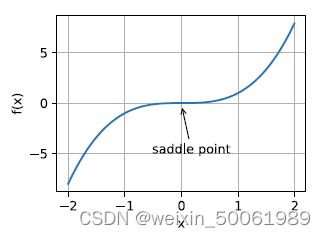
         鞍点指函数的所有梯度都消失但既不是全局最⼩值也不是局部最⼩值的任何位置。如图：

鞍点

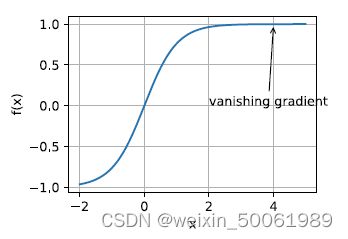
        可能遇到的最隐蔽问题是梯度消失。例如，假设我们想最⼩化函数f(x) = tanh(x)，然后我们恰好从x = 4开始。正如我们所看到的那样，f的梯度接近零。更具体地说，，因此是f′(4) = 0:0013。因此，在我们取得进展之前，优化将会停滞很⻓⼀段时间。事实证明，这是在引⼊ReLU激活函数之前训练深度学习模型相当棘⼿的原因之⼀。

梯度消失

         有一系列算法表现良好。实际上没有必要找到最优解。局部最优解或其近似解仍然⾮常有⽤。

1、Momentum method

        随机梯度下降(SGD)可能会遇到病态曲率问题。

病态曲率

        图为损失函数轮廓。在进入以蓝色标记的山沟状区域之前随机开始。颜色实际上表示损失函数在特定点处的值有多大， 红色表示最大值，蓝色表示最小值。我们想要达到最小值点，为此但需要我们穿过山沟。这个区域就是所谓的病态曲率。

        梯度下降沿着山沟的山脊反弹，向极小的方向移动较慢。这是因为脊的表面在这个方向上弯曲得更陡峭。

        使用泄露平均值(leaky average)代替梯度计算：

        v被称为动量。

        如果把原始的 SGD 想象成一个纸团在重力作用向下滚动，由于质量小受到山壁弹力的干扰大，导致来回震荡；或者在鞍点处因为质量小速度很快减为 0 ，导致无法离开这块平地。
        动量方法相当于把纸团换成了铁球；不容易受到外力的干扰，轨迹更加稳定；同时因为在鞍点处因为惯性的作用，更有可能离开平地。

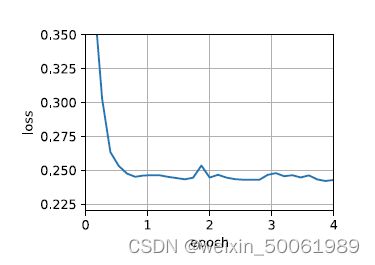
         利用深度学习框架，给出动量法的简洁实现：

%matplotlib inline
import torch
from d2l import torch as d2l

trainer = torch.optim.SGD
d2l.train_concise_ch11(trainer, {'lr': 0.005, 'momentum': 0.9}, data_iter)

 2、Adaptive Gradient

        参数自适应变化：具有较大偏导的参数相应有一个较大的学习率，而具有小偏导的参数则对应一个较小的学习率。

AdaGrad

         这种算法存在问题：学习率是单调递减的，训练后期学习率过小会导致训练困难，甚至提前结束。

3、RMSProp: Root Mean Square Prop

        使用RMSProp对于AdaGrad进行改善，按照动量法中的方式使用泄露平均值，对于AdaGrad进行修改。

RMSProp

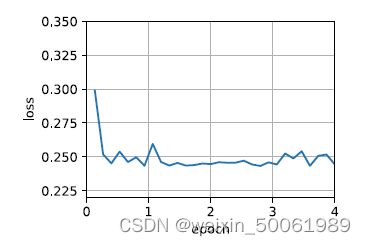
         给出RMSProp简洁实现。

import math
import torch
from d2l import torch as d2l

trainer = torch.optim.RMSprop
d2l.train_concise_ch11(trainer, {'lr': 0.01, 'alpha': 0.9}, data_iter)

 4、Adam算法

        回顾其他优化算法：随机梯度下降在解决优化问题时⽐梯度下降更有效。在⼀个⼩批量中使⽤更⼤的观测值集，可以通过向量化提供额外效率。这是⾼效的多机、多GPU和整体并⾏处理的关键。添加了⼀种机制，⽤于汇总过去梯度的历史以加速收敛。对每个坐标缩放来实现⾼效计算的预处理器。学习率的调整来分离每个坐标的缩放。

        Adam算法将这些优点进行汇总，是一种更强大和更有效的优化算法。但是仍存在问题，可能由于方差控制不良而发散。

        除了加入历史梯度平方的指数衰减平均()外还保留了历史梯度的指数衰减平均()，相当于动量。

        Adam 行为就像一个带有摩擦力的小球，在误差面上倾向于平坦的极小值。

Adam

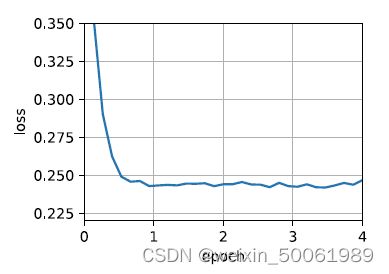
         简洁实现：

%matplotlib inline
import torch
from d2l import torch as d2l

trainer = torch.optim.Adam
d2l.train_concise_ch11(trainer, {'lr': 0.01}, data_iter)

---

总结

        主要对于深度学习的基础Multilayer Perception和一些优化算法进行了学习，主要参考了《动手学深度学习》，跟多代码科技参考这本书。