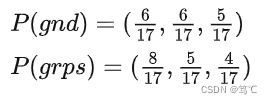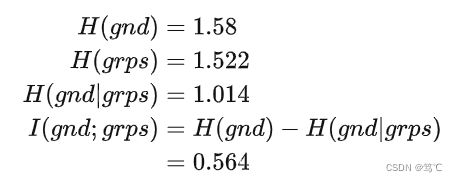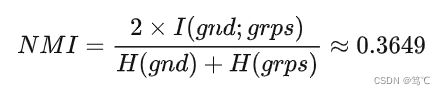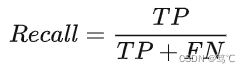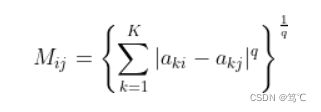【聚类指标】如何评估聚类算法：外部指标和内部指标、指标详解
【聚类指标】如何评估聚类算法：外部指标和内部指标、指标详解
文章目录
- 【聚类指标】如何评估聚类算法：外部指标和内部指标、指标详解
-
- 1. 前言
- 2. 外部指标
-
- 2.1 P（Purity）
-
- 2.1.1 例子
- 2.2 NMI（Normalized Mutual Information）
-
- 2.2.1 例子
- 2.3 对混淆矩阵（RI、Precision、Recall、F）
-
- 2.3.1 RI（兰德系数）
- 2.3.2 Precision（精确度）
- 2.3.3 Recall（召回率）
- 2.3.4 F值（平衡精确度与召回率）
- 2.3.5 例子
- 2.4 ARI（调整兰德系数）
- 2.5 AC（Accuracy）
- 3. 内部指标
-
- 3.1 紧密度（Compactness）
- 3.2 分割度（Seperation）
- 3.3 误差平方和 （SSE：Sum of squares of errors）
- 3.4 轮廓系数（SC）
- 3.5 Calinski-Harabaz 指数（CH）
- 3.6 Davies-Bouldin Index（DB）
- 4. 参考
1. 前言
一个好的聚类方法可以产生高品质簇，是的簇内相似度高，簇间相似度低。一般来说，评估聚类质量有两个标准，外部评价指标和内部评价指标。
- 外部指标，也就是有参考标准的指标，通常也可以称为有监督情况下的一种度量聚类算法和各参数的指标。具体就是聚类算法的聚类结果和已知的（有标签的、人工标准或基于一种理想的聚类的结果）相比较，从而衡量设计的聚类算法的性能、优劣。
- 内部指标是无监督的，无需基准数据集，不需要借助于外部参考模型，利用样本数据集中样本点与聚类中心之间的距离来衡量聚类结果的优劣。
2. 外部指标
外部质量评价指标是基于已知分类标签数据集进行评价的，这样可以将原有标签数据与聚类输出结果进行对比。
- 外部质量评价指标的理想聚类结果是：具有不同类标签的数据聚合到不同的簇中，具有相同类标签的数据聚合相同的簇中。外部质量评价准则通常使用熵，纯度等指标进行度量。
2.1 P（Purity）
在聚类结果的评估标准中，一种最简单最直观的方法就是计算它的聚类纯度（purity），别看纯度听起来很陌生，但实际上分类的准确率有着异曲同工之妙。因为聚类纯度也用聚类正确的样本数除以总的样本数。
- 但是对于聚类后的结果我们并不知道每个簇所对应的真实类别，因此需要取每种情况下的最大值。（注意与聚类准确率的区别：计算聚类准确率需要知道每个簇的真实类别，一一对应关系）。
具体的，纯度（Purity）的计算公式定义如下：
其中, N 表示总的样本个数， Ω = { w 1 , w 2 , . . . , w K } \Omega = \{ w_1, w_2,...,w_K\} Ω={w1,w2,...,wK}表示聚类簇 (cluster) 划分， C = { c i , c 2 , . . . , c J } C = \{ c_i, c_2,...,c_J\} C={ci,c2,...,cJ}表示真实类别 (class) 划分。
- 上述过程即给每个「聚类簇」分配一个「类别」,且「为这个类别的样本」在该簇中「出现的次数最多」,然后计算所有 K 个聚类簇的这个次数之和再归一化即为最终值。
- P u r i t y ∈ [ 0 , 1 ] Purity \in [0, 1] Purity∈[0,1]，越接近1表示聚类结果越好。
- 该值无法用于权衡聚类质量与簇个数之间的关系。
2.1.1 例子
2.2 NMI（Normalized Mutual Information）
NMI (Normalized Mutual Information) 即归一化互信息。
其中, I I I 表示互信息(Mutual Information), H 为熵，当 log 取 2 为底时，单位为 bit，取 e 为底时单位为 nat。
其中, P ( w k ) , P ( c j ) , P ( w k ∩ c j ) P(w_k), P(c_j), P(w_k ∩ c_j) P(wk),P(cj),P(wk∩cj)可以分别看作样本 (document) 属于聚类簇 w k w_k wk, 属于类别 c j c_j cj, 和同时属于两者的概率。第二个等价式子则是由概率的极大似然估计推导而来。
互信息 I ( Ω ; C ) I(\Omega; C) I(Ω;C) 表示给定类簇信息 C C C 的前提条件下，类别信息 Ω \Omega Ω的增加量，或者说其不确定度的减少量。直观地，互信息还可以写出如下形式：
- 互信息的最小值为 0，当类簇相对于类别只是随机的，也就是说两者独立的情况下, Ω \Omega Ω对于 C C C未带来任何有用的信息；
- 如果得到的 Ω \Omega Ω 与 C C C关系越密切, 那么 I ( Ω ; C ) I(\Omega; C) I(Ω;C)值越大。如果 Ω \Omega Ω完整重现了 C C C， 此时互信息最大。
- 当 K = N K=N K=N时，即类簇数和样本个数相等，MI 也能达到最大值。所以 MI 也存在和纯度类似的问题，即它并不对簇数目较大的聚类结果进行惩罚，因此也不能在其他条件一样的情况下，对簇数目越小越好的这种期望进行形式化。
NMI则可以解决上述问题，因为熵会随着簇的数目的增长而增大。当 K = N K=N K=N时， H ( Ω ) H(\Omega) H(Ω)会达到其最大值 l o g N log N logN，此时就能保证 NMI 的值较低。之所以采用 ( H ( Ω ) + H ( C ) ) / 2 (H(\Omega) + H(C))/2 (H(Ω)+H(C))/2 作为分母，是因为它是 I ( Ω ; C ) I(\Omega; C) I(Ω;C)的紧上界，因此可以保证 NMI ∈[0, 1]。
2.2.1 例子
- 1）先计算联合概率分布 p ( g r p s , g n d ) p(grps, gnd) p(grps,gnd)
- 2）计算边际分布
- 3）计算熵和互信息
- 4）计算 NMI
2.3 对混淆矩阵（RI、Precision、Recall、F）
与分类问题中的混淆矩阵类似，对于聚类问题中的对混淆矩阵，我们可以做出如下定义：
-
TP：表示两个同类样本点在同一个簇（布袋）中的情况数量；
-
FP：表示两个非同类样本点在同一个簇中的情况数量；
-
TN：表示两个非同类样本点分别在两个簇中的情况数量；
-
FN：表示两个同类样本点分别在两个簇中的情况数量；
-
正确决策:
- TP 将两篇相似文档归入一个簇 (同 - 同)
- TN 将两篇不相似的文档归入不同的簇 (不同 - 不同)
-
错误决策:
- FP 将两篇不相似的文档归入同一簇 (不同 - 同)
- FN 将两篇相似的文档归入不同簇 (同- 不同) (worse)
2.3.1 RI（兰德系数）
2.3.2 Precision（精确度）
2.3.3 Recall（召回率）
2.3.4 F值（平衡精确度与召回率）
2.3.5 例子
- 1）计算TP、FP、TN、FN：
- TP 表示两个同类样本点在同一个簇中的情况数量，因此根据图1中的聚类结果有：
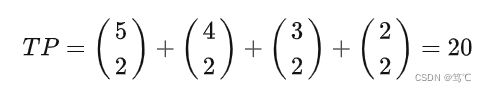
其表示的含义是，对于簇1来说5个叉形中取2个的情况；对于簇2来说4个圆形中取2个的情况；对于簇3来说3个菱形中取2个；以及2个叉形中取2个的情况。 - 注意：在计算完成TP后，我们发现其它三种情况都无法单独的进行计算了（因为都是交叉混合的情况），因此我们可以同时计算多种组合下的情况数。
- 由四种情况的定义可知，TP+FP 表示的是同一簇中任取两个样本点的情况数（包含了同类和非同类），因此根据图中的聚类结果有：
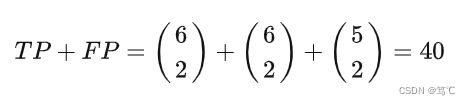
- 同理，TP+TN 表示的就是任意两个同类样本点分布在同一个簇和非同一个簇的所有情况总和，所以有：
- 同时，根据前面的分析可知，对于聚类后的结果，不管你是在某一个簇中任取2个样本，还是说你在任意不同的2个簇中各取1个样本，所有可能出现的情况都只会有上面的四种，所以有：
- 由此，我们便可以分别计算出：
- TP 表示两个同类样本点在同一个簇中的情况数量，因此根据图1中的聚类结果有：
- 2）求RI、Precision、Recall、F
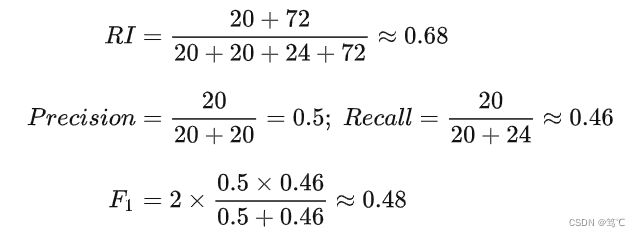
2.4 ARI（调整兰德系数）
调整兰德系数（ARI）是兰德系数（RI）的一个改进版本，目的是为了去掉随机标签对于兰德系数评估结果的影响。
- 例如对于图中的17个样本，你随机将每个样本都划到一个簇中（也就是17个簇）。那么其计算出来的兰德系数仍旧是0.68，此时的 TP=0, FP=0, FN=44, TN=92。
那具体的ARI该怎么计算呢？下面我们还是以上图中的聚类结果为例来进行讲解。
如上图所示， X X X(cluster) 表示聚类算法认为的聚类结果，每个圆圈代表一个簇；而 Y Y Y 表示我们根据正确标签对聚类结果标记后的结果（也就是每个样本的形状，形状一样则属于同一类）。因此，根据聚类得到的结果和真实标签我们便能得到如下所示的列联表（ contingency table）：
其中 X = { X 1 , X 2 , . . . , X r } X = \{X_1,X_2,...,X_r\} X={X1,X2,...,Xr}表示聚类得到 r 个簇的集合，而 Y = { Y 1 , Y 2 , . . . , Y s } Y = \{Y_1,Y_2,...,Y_s\} Y={Y1,Y2,...,Ys}表示根据样本正确标签对聚类结果修正后的集合，
n i j n_{ij} nij表示 X i X_i Xi 与 Y j Y_j Yj相交部分的样本数量，即 n i j = X i ∩ Y j n_{ij} = X_i ∩ Y_j nij=Xi∩Yj。
根据这张列联表我们便能够得到ARI的计算公式：
其中 ARI 的取值范围为[-1, 1]，越大也就表示聚类效果越好。
虽然上面这张表和公式开起来很复杂，但其实只要你看一遍具体的计算过程就会发现也就那么回事。我们就能够得到如下所示的列联表：
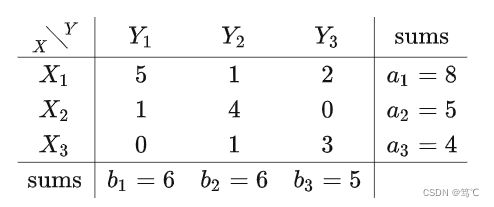
根据此表可得：
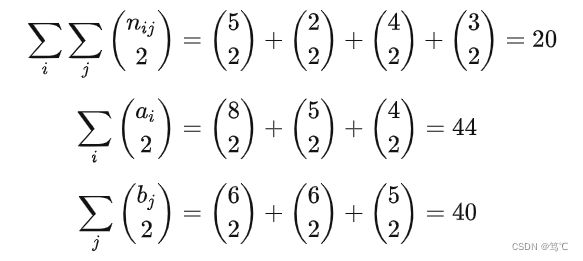
所以有：
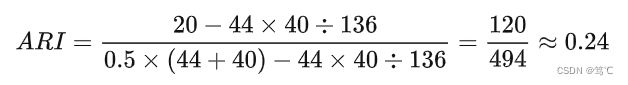
同时，根据各部分的意义我们还可以将公式写成：
2.5 AC（Accuracy）
Purity, NMI, RI 等上述指标均需要给定 truth label 才能对 cluster label 进行评价，但是均不要求后者的类标与前者一致。那什么时候需要进行类标签的 best map 呢？例如，我们需要对预测结果和真实值之间统计聚类正确的比例时就需要进行最佳类标的重现分配，这样才能保证统计的正确。
聚类精确度 (Accuracy, AC) 用于比较获得标签和数据提供的真实标签。
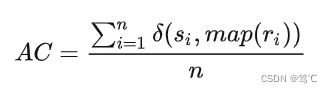
其中， r i , s i r_i, s_i ri,si 分别表示数据 x i x_i xi所对应的获得的标签和真实标签， n n n 为数据总的个数， δ \delta δ 表示指示函数如下：
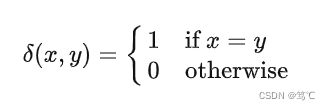
而式中的 map 则表示最佳类标的重现分配，以才能保证统计的正确。一般的该最佳重分配可以通过匈牙利算法 (Kuhn-Munkres or Hungarian Algorithm) 实现，从而在多项式时间内求解该任务（标签）分配问题。
3. 内部指标
内部评价指标是利用数据集的属性特征来评价聚类算法的优劣。通过计算总体的相似度，簇间平均相似度或簇内平均相似度来评价聚类质量。
- 评价聚类效果的高低通常使用聚类的有效性指标，所以目前的检验聚类的有效性指标主要是通过簇间距离和簇内距离来衡量。这类指标常用的有CH（Calinski-Harabasz）指标等。
3.1 紧密度（Compactness）
紧密度（Compactness）：每个聚类簇中的样本点到聚类中心的平均距离。对应聚类结果，需要使用所有簇的紧密度的平均值来衡量聚类算法和聚类各参数选取的优劣。紧密度越小，表示簇内的样本点越集中，样本点之间聚类越短，也就是说簇内相似度越高。
3.2 分割度（Seperation）
分割度（Seperation）：是个簇的簇心之间的平均距离。分割度值越大说明簇间间隔越远，分类效果越好，即簇间相似度越低。
3.3 误差平方和 （SSE：Sum of squares of errors）
误差平方和 （SSE：Sum of squares of errors）：类中数据聚类距离类中心的平方损失之和，即K-means算法的优化目标，表示为：
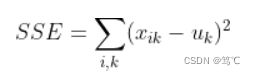
其中， x i k x_{ik} xik表示第k个类中第i个样本点， u k u_k uk表示第k个类的中心点。
3.4 轮廓系数（SC）
轮廓系数（Silhouette Coefficient）是聚类效果好坏的一种评价方式。轮廓系数取值范围为[-1,1]，取值越接近1则说明聚类性能越好，相反，取值越接近-1则说明聚类性能越差。为了求SC，我们作出以下定义：
- a：某个样本与其所在簇内其他样本的平均距离；
- b：某个样本与其他簇样本的平均距离；
则，针对某个样本的轮廓系数s为：
而聚类总的轮廓系数SC为：
-
轮廓系数优点：
- 轮廓系数为-1时表示聚类结果不好，为+1时表示簇内实例之间紧凑，为0时表示有簇重叠。
- 轮廓系数越大，表示簇内实例之间紧凑，簇间距离大，这正是聚类的标准概念。
-
轮廓系数的缺点：
- 对于簇结构为凸的数据轮廓系数值高，而对于簇结构非凸需要使用DBSCAN进行聚类的数据，轮廓系数值低。
- 因此，轮廓系数不应该用来评估不同聚类算法之间的优劣，比如Kmeans聚类结果与DBSCAN聚类结果之间的比较。
3.5 Calinski-Harabaz 指数（CH）
Calinski-Harabasz指数的本质是：簇间距离与簇内距离的比值，且整体计算过程与方差计算方式类似，所以又将其称之为方差比准则。
- 将容量为 N 的数据集合 X 聚成 K 类，通过计算类内各点与类中心的距离平方和来度量类内的紧密度（类内距离），各个类中心点与数据集中心点距离平方和来度量数据集的分离度（类间距离）。
CH指标的计算公式为：
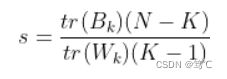
其中 B k B_k Bk为类间的协方差矩阵， W k W_k Wk类内数据的协方差矩阵，详细公式如下：
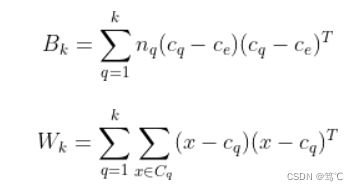
其中 c q c_q cq表示类q的中心点， c e c_e ce表示数据集的中心点， n q n_q nq表示类q中的数据的数目， C q C_q Cq表示类q的数据集合。
Calinski-Harabasz指数的分数越大说明越好（类别内部协方差越小越好，类别之间协方差越大越好）。
3.6 Davies-Bouldin Index（DB）
Davies-Bouldin Index（由大卫L·戴维斯和唐纳德·Bouldin提出）是一种评估是一种评估度量的聚类算法。
DB计算任意两类别的类内距离平均之和除以该两类中心距离，并求最大值。DB越小意味着类内距离越小同时类间距离越大。
其中 s i s_i si表示类中样本点分散度， M i j M_{ij} Mij则就是第 i 类与第 j 类中心的距离。计算公式如下所示：
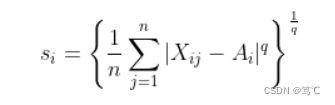
其中 X i j X_{ij} Xij表示第 i 类中第 j 个数据点； A i A_i Ai表示第 i 类的中心；n表示第i类中数据点的个数；
- q取1表示：各点到中心的距离的均值，q取2时表示：各点到中心距离的标准差，它们都可以用来衡量分散程度。
其中 a k i a_{ki} aki表示第i类的中心点的第K个属性的值。
4. 参考
【1】https://zhuanlan.zhihu.com/p/53840697
【2】https://zhuanlan.zhihu.com/p/343667804
【3】https://blog.csdn.net/xiaolong124/article/details/126345406