计算几何--简单多边形与圆面积交

求解二维空间内一个简单多边形和一个长度为R的圆公共面积。

因为任意简单多边形都可以划分成若干三角形，我们可以把这个简单多边形划分成三角形后，求三角形与圆的面积交，然后在把所有三角形的解合并。

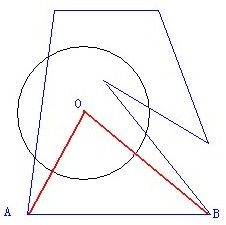
由于可能有凹多边形，我们计算三角形与圆面积交时采用向量叉乘，这样得到的是一个有向面积，刚好可以把凹多边形面积正负抵消掉，最后把总面积取绝对值就行了。

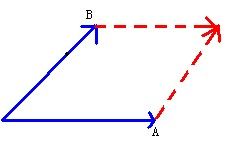
向量叉乘 A x B == 以向量A,B为2邻边，围城平行四边形的有向面积。  A在B顺时针方向值为正，逆时针为负。

AxB==

|A.x  ,  A.y |

|B.x  ,  B.y |

==A.x*B.y-A.y*B.x

 

计算一个圆与一个三角形的面积交(其中一个三角形顶点是圆心，如上图)，我采用的方法是分4种情况。

 

1.

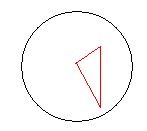另外2个顶点在圆内（上），这个非常好算直接求三角形的有向面积即可。

2.

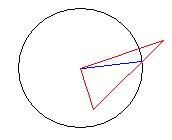
另外两个顶点有1个再圆内（上）,另外1个再圆外，求得直线与圆一个交点后求一个三角形面积+上一个扇形面积。

3.

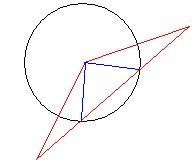
2个顶点在圆外，且2个顶点所在边与圆相交，先求圆外2顶点所在直线与圆交点，然后定比分点公式求另外2条直线与圆交点，然后求一个三角形+2个扇形面积即可。

 

4.

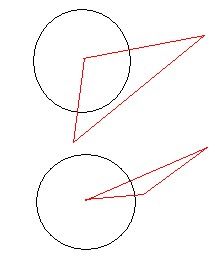
2个顶点都在圆外且2顶点所在边与圆不相交，这个情况求2个交点后算出那个扇形面积就行了。

 

下面是我写的圆与三角形有向面积交函数，注意三角形其中一个顶点在圆心，如果都不在圆心，可以把这个三角形在划分成3个其中一个顶点在圆心的三角形求解。

  1 /**************************************

  2 Author : lxgsbqylbk

  3 Date : 2012/08/12

  4 Function : Direct area of a circle and triangle

  5 ***********/

  6 const double eps = 1e-8;            //浮点数精度控制

  7 

  8 struct point                        //点或者向量结构

  9 {

 10     double x,y;

 11     point(double _x=0.0,double _y=0.0)

 12         : x(_x),y(_y) {}

 13     point operator - (const point & v)

 14     {

 15         return point(x-v.x,y-v.y);

 16     }

 17     double sqrx()                    //向量的模

 18     {

 19         return sqrt(x*x+y*y);

 20     }

 21 };

 22 double xmult(point & p1,point & p2,point & p0)        //叉乘

 23 {

 24     return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);

 25 }

 26 double distancex(point & p1,point & p2)

 27 {

 28     return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));

 29 }

 30 point intersection(point u1,point u2,point v1,point v2)        //两直线交点

 31 {

 32     point ret=u1;

 33     double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))

 34             /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));

 35     ret.x+=(u2.x-u1.x)*t;

 36     ret.y+=(u2.y-u1.y)*t;

 37     return ret;

 38 }

 39 void intersection_line_circle(point c,double r,point l1,point l2,point& p1,point& p2){

 40     point p=c;

 41     double t;

 42     p.x+=l1.y-l2.y;

 43     p.y+=l2.x-l1.x;

 44     p=intersection(p,c,l1,l2);

 45     t=sqrt(r*r-distancex(p,c)*distancex(p,c))/distancex(l1,l2);

 46     p1.x=p.x+(l2.x-l1.x)*t;

 47     p1.y=p.y+(l2.y-l1.y)*t;

 48     p2.x=p.x-(l2.x-l1.x)*t;

 49     p2.y=p.y-(l2.y-l1.y)*t;

 50 }

 51 point ptoseg(point p,point l1,point l2)            //点到线段的最近距离

 52 {

 53     point t=p;

 54     t.x+=l1.y-l2.y,t.y+=l2.x-l1.x;

 55     if (xmult(l1,t,p)*xmult(l2,t,p)>eps)

 56     return distancex(p,l1)<distancex(p,l2)?l1:l2;

 57     return intersection(p,t,l1,l2);

 58 }

 59 double distp(point & a,point & b)

 60 {

 61     return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);

 62 }

 63 double Direct_Triangle_Circle_Area(point a,point b,point o,double r)

 64 {

 65     double sign=1.0;

 66     a=a-o;

 67     b=b-o;

 68     o=point(0.0,0.0);

 69     if(fabs(xmult(a,b,o))<eps) return 0.0;

 70     if(distp(a,o)>distp(b,o))

 71     {

 72         swap(a,b);

 73         sign=-1.0;

 74     }

 75     if(distp(a,o)<r*r+eps)

 76     {

 77         if(distp(b,o)<r*r+eps) return xmult(a,b,o)/2.0*sign;

 78         point p1,p2;

 79         intersection_line_circle(o,r,a,b,p1,p2);

 80         if(distancex(p1,b)>distancex(p2,b)) swap(p1,p2);

 81         double ret1=fabs(xmult(a,p1,o));

 82         double ret2=acos( p1*b/p1.sqrx()/b.sqrx() )*r*r;

 83         double ret=(ret1+ret2)/2.0;

 84         if(xmult(a,b,o)<eps && sign>0.0 || xmult(a,b,o)>eps && sign<0.0) ret=-ret;

 85         return ret;

 86     }

 87     point ins=ptoseg(o,a,b);

 88     if(distp(o,ins)>r*r-eps)

 89     {

 90         double ret=acos( a*b/a.sqrx()/b.sqrx() )*r*r/2.0;

 91         if(xmult(a,b,o)<eps && sign>0.0 || xmult(a,b,o)>eps && sign<0.0) ret=-ret;

 92         return ret;

 93     }

 94     point p1,p2;

 95     intersection_line_circle(o,r,a,b,p1,p2);

 96     double cm=r/(distancex(o,a)-r);

 97     point m=point( (o.x+cm*a.x)/(1+cm) , (o.y+cm*a.y)/(1+cm) );

 98     double cn=r/(distancex(o,b)-r);

 99     point n=point( (o.x+cn*b.x)/(1+cn) , (o.y+cn*b.y)/(1+cn) );

100     double ret1 = acos( m*n/m.sqrx()/n.sqrx() )*r*r;

101     double ret2 = acos( p1*p2/p1.sqrx()/p2.sqrx() )*r*r-fabs(xmult(p1,p2,o));

102     double ret=(ret1-ret2)/2.0;

103     if(xmult(a,b,o)<eps && sign>0.0 || xmult(a,b,o)>eps && sign<0.0) ret=-ret;

104     return ret;

105 }