吴恩达《机器学习》笔记——第六章《逻辑回归/对数几率回归》
6、Logistic Regression(逻辑回归/对数几率回归)
- 6.1 Classification(分类)
- 6.2 Hypothesis Representation(假设表示)
- 6.3 Decision boundary(决策边界)
- 6.4 Cost function(代价函数)
- 6.5 Simplified cost function and gradient descent(简化代价函数与梯度下降)
- 6.6 Advanced optimization(高级优化)
- 6.7 Multi-class classification One-vs-all(多元分类:一对多)
6.1 Classification(分类)
Logistic回归虽然被称为“回归”,但是它是一个“分类”算法,用在预测值为离散值 0 0 0或 1 1 1的情况下。
6.2 Hypothesis Representation(假设表示)
当有一个分类问题时,用什么方程去表示该问题对应的假设?
Logistic Regression Model 想要 0 ≤ h θ ( x ) ≤ 1 0\leq h_\theta(x)\leq1 0≤hθ(x)≤1。令 h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx),其中 g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1称为Sigmoid函数或Logistic函数。Sigmoid函数的图像如图所示:
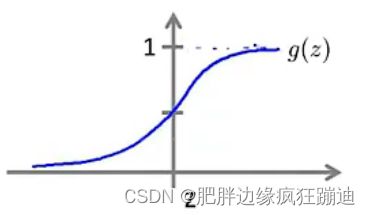
假设函数 h θ ( x ) h_\theta(x) hθ(x)输出的解释: h θ ( x ) = h_\theta(x)= hθ(x)= estimated probability that y = 1 y=1 y=1 on input x x x,即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x)=P(y=1|x;\theta) hθ(x)=P(y=1∣x;θ),因为 y y y只能取值 0 0 0或 1 1 1,所以 P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) P(y=0|x;\theta)=1-h_\theta(x) P(y=0∣x;θ)=1−hθ(x)。
注:上述的 θ = ( θ 0 , θ 1 , ⋯ , θ n ) T , x = ( x 0 , x 1 , ⋯ , x n ) , x 0 = 1 \theta=(\theta_0,\theta_1,\cdots,\theta_n)^T,x=(x_0,x_1,\cdots,x_n),x_0=1 θ=(θ0,θ1,⋯,θn)T,x=(x0,x1,⋯,xn),x0=1。
6.3 Decision boundary(决策边界)
假设预测 y = 1 y=1 y=1,如果 h θ ( x ) ≥ 0.5 h_\theta(x)\geq0.5 hθ(x)≥0.5;预测 y = 0 y=0 y=0,如果 h θ ( x ) < 0.5 h_\theta(x)<0.5 hθ(x)<0.5。由Sigmoid函数, g ( z ) ≥ 0.5 ⟺ z ≥ 0 , g ( z ) < 0.5 ⟺ z < 0 g(z)\geq0.5\iff z\geq0,g(z)<0.5\iff z<0 g(z)≥0.5⟺z≥0,g(z)<0.5⟺z<0 其中 z z z是关于 x , θ x,\theta x,θ的函数 z ( x , θ ) z(x,\theta) z(x,θ),比如6.1, z ( x , θ ) = θ T x z(x,\theta)=\theta^Tx z(x,θ)=θTx。 z ( x , θ ) = 0 z(x,\theta)=0 z(x,θ)=0被称为决策边界。
注: z ( x , θ ) z(x,\theta) z(x,θ)可以是多项式。决策边界不是训练集的属性,而是假设本身及其参数的属性。
6.4 Cost function(代价函数)
对于线性回归: J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{m}\sum_{i=1}^m\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=m1∑i=1m21(hθ(x(i))−y(i))2。令 C o s t ( h θ ( x ( i ) ) , y ( i ) ) = 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 Cost(h_\theta(x^{(i)}),y^{(i)})=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 Cost(hθ(x(i)),y(i))=21(hθ(x(i))−y(i))2。
注:其实所有回归的代价函数都可写成 J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) J(θ)=m1∑i=1mCost(hθ(x(i)),y(i))的形式。
如果直接使用逻辑回归的假设函数替代线性回归中的假设函数,则 J ( θ ) J(\theta) J(θ)是非凸的。所以,希望构造一个 C o s t ( h θ ( x ) , y ) Cost(h_\theta(x),y) Cost(hθ(x),y)使得 J ( θ ) J(\theta) J(θ)是凸的。对于逻辑回归,令 C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) , if y = 1 − l o g ( 1 − h θ ( x ) ) , if y = 0 Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x)),&\text{if }y=1 \\ -log(1-h_\theta(x)),&\text{if }y=0 \end{cases} Cost(hθ(x),y)={−log(hθ(x)),−log(1−hθ(x)),if y=1if y=0 则该 C o s t ( h θ ( x ) , y ) Cost(h_\theta(x),y) Cost(hθ(x),y)使得 J ( θ ) J(\theta) J(θ)是凸的。
6.5 Simplified cost function and gradient descent(简化代价函数与梯度下降)
由6.6知, J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) J(θ)=m1∑i=1mCost(hθ(x(i)),y(i)), C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) , if y = 1 − l o g ( 1 − h θ ( x ) ) , if y = 0 Cost(h_\theta(x),y)=\begin{cases} -log(h_\theta(x)),&\text{if }y=1\\-log(1-h_\theta(x)),&\text{if }y=0 \end{cases} Cost(hθ(x),y)={−log(hθ(x)),−log(1−hθ(x)),if y=1if y=0,
可以将 C o s t ( h θ ( x ) , y ) Cost(h_\theta(x),y) Cost(hθ(x),y)简化为
C o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x)) Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x)) 则 J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})=-\frac{1}{m}\sum_{i=1}^m[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
利用梯度下降算法最小化 J ( θ ) J(\theta) J(θ),有 θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta) θj:=θj−α∂θj∂J(θ)。对于 h θ ( x ) = 1 1 + e − θ T x h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=1+e−θTx1,有 ∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial}{\partial\theta_j}J(\theta)=\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} ∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)在求解时,可以把上述所有的 θ j \theta_j θj 组成向量求解。
注:第四章提到过的特征缩放和调整学习率也可以用在这。
6.6 Advanced optimization(高级优化)
就是提了除了梯度下降法最小化代价函数外,还有其它更好的方法来优化代价函数,比如共轭梯度法、BFGS、L-BFGS。这些都可以在数值优化的书上找到。
6.7 Multi-class classification One-vs-all(多元分类:一对多)
本文介绍了一个简单的使用逻辑回归解决多类别分类问题,该算法称为“一对多”的分类算法。
Idea:对于有着 n n n个分类的多分类问题 { y = i } i = 1 n \{y=i\}_{i=1}^n {y=i}i=1n,学习 n n n个逻辑回归分类器 { h θ i ( x ) = P ( y = i ∣ x ; θ ) } i = 1 n \{h_\theta^i(x)=P(y=i|x;\theta)\}_{i=1}^n {hθi(x)=P(y=i∣x;θ)}i=1n。在训练 h θ i ( x ) h_\theta^i(x) hθi(x)时,相当于是一个二分类,把 y = i y=i y=i看做 y = 1 y=1 y=1,其它训练样本看作 y = 0 y=0 y=0。
对于新输入的 x x x,做预测时,选择使得 h θ i ( x ) h_\theta^i(x) hθi(x)最大的 i i i,即 max i h θ i ( x ) \mathop{\max}\limits_{i}h_\theta^i(x) imaxhθi(x)。