Note_001 数据操作【深度学习_学习笔记】
文章目录
- 一、基本概念
- 二、函数解析
-
- 运算符
- 广播机制
- 索引和切片
- 节省内存
- 转换为其他Python对象
- 小结
- 练习
- 练习答案
- 要学习深度学习,首先应该掌握一些基本技能。所有机器学习方法都涉及从数据中提取信息。 因此,我们先学习一些关于数据的实用技能,包括存储、操作和预处理数据。
一、基本概念
N维数组 :也称为张量(tensor), 无论哪个深度学习框架,它的张量类(在MXNet中为ndarray, 在PyTorch和TensorFlow中为(Tensor)都与Numpy的ndarray类似,另外,深度学习框架比Numpy的ndarray多一些重要功能,这些功能使得张量类更适合深度学习
- GPU很好地支持加速计算,而NumPy仅支持CPU计算
- 张量类支持自动微分
张量表示一个由数值组成的数组,这个数组可能有多个维度 具有一个轴的张量对应数学上的向量(vector) 具有两个轴的张量对应数学上的矩阵(matrix) 具有两个轴以上的张量没有特殊的数学名称
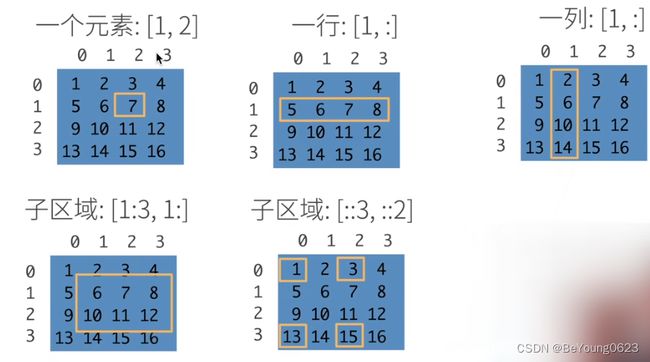
访问数组:
- 语法列表[起始 : 结束 : 步长]
- “::”这个形式有三个参数,前两个是左闭右开的区间,第三个是步长(可省略,默认为1)
- 左闭右开区间:在通过切片获取元素时,会包括起始位置的元素,不会包括结束位置的元素
- 起始位置和结束位置的索引可以不写如果省略结束位置, 则会从当前的开始位置一直截取到最后
- 如果省略开始位置, 则会从第一个元素截取到结束的元素,但是不包括结束的元素
- 如果开始位置和结束位置都省略, 则则会从第一个元素开始截取到最后一个元素
二、函数解析
import torch
x = torch.arange(12) # 用于生成一个整数序列
print(x.shape) # torch.Size([12])
# 如果只想知道张量中元素的总数,即形状的所有元素乘积,可以检查它的大小(size)
# 因为这里在处理的是一个向量,所以它的shape与它的size相同
print(x.numel()) # 12
X = x.reshape(3, 4) # 要想改变一个张量的形状而不改变元素数量和元素值,可以调用reshape函数
# 我们可以用x.reshape(-1,4)或x.reshape(3,-1)来取代x.reshape(3,4)
print(X)
print(torch.zeros((2, 3, 4))) # 有时,我们希望[使用全0、全1、其他常量,或者从特定分布中随机采样的数字]来初始化矩阵。
# 我们可以创建一个形状为(2,3,4)的张量,其中所有元素都设置为0。
print(torch.ones((2, 3, 4))) # 我们可以创建一个形状为(2,3,4)的张量,其中所有元素都设置为1
print(torch.randn(3, 4)) # 有时我们想通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。
# 例如,当我们构造数组来作为神经网络中的参数时,我们通常会随机初始化参数的值。
# 本行代码创建一个形状为(3,4)的张量。 其中的每个元素都从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。
print(torch.tensor([[2, 1, 4, 3],
[1, 2, 3, 4],
[4, 3, 2, 1]])) # 通过提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值
运算符
import torch
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
print(x + y, "\n" , x - y, "\n" ,
x * y , "\n", x / y, "\n",
x ** y) # **运算符是求幂运算
# 对于任意具有相同形状的张量
# 常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算(相同位置的元素进行计算)
print(torch.exp(x)) # “按元素”方式可以应用更多的计算,包括像求幂这样的一元运算符
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(torch.cat((X, Y), dim=0),"\n",torch.cat((X, Y), dim=1)) # 我们也可以把多个张量连结(concatenate)在一起
# 把它们端对端地叠起来形成一个更大的张量
# 我们只需要提供张量列表,并给出沿哪个轴连结
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]]) 3 + 3 = 6 行
# tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]]) 4 + 4 = 8 列
print(X == Y) # 按元素位置比对(要求是同型矩阵)
# tensor([[False, True, False, True],
# [False, False, False, False],
# [False, False, False, False]])
print(X.sum()) # 对张量中的所有元素进行求和,会产生一个单元素张量
# tensor(66.)
广播机制
上面部分中的元素操作,要求两个张量具有相同的形状。 在某些情况下,即使形状不同,我们仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作
- 通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状
- 对生成的数组执行按元素操作
当对两个 array 进行操作时,numpy 会逐元素比较它们的形状。
从尾(即最右边)维度开始,然后向左逐渐比较。
只有当两个维度相等或者其中一个维度是1 时,这两个维度才会被认为是兼容。
如果不满足这些条件,则会抛出 ValueError:operands could not be broadcast together 异常,表明 array 的形状不兼容。最终结果 array 的每个维度尽可能不为 1 ,是两个操作数各个维度中较大的值 。
import torch
a = torch.arange(6).reshape((3, 2))
b = torch.arange(2).reshape((1, 2))
print(a, "\n" ,b) # tensor([[0, 1],
# [2, 3],
# [4, 5]])
# tensor([[0, 1]])
print(a + b) # tensor([[0, 2],
# [2, 4],
# [4, 6]])
索引和切片
就像在任何其他Python数组中一样,张量中的元素可以通过索引访问。 与任何Python数组一样:第一个元素的索引是0,最后一个元素索引是-1; 可以指定范围以包含第一个元素和最后一个之前的元素
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
print(X[-1], "\n" ,X[1:3]) # 可以用[-1]选择最后一个元素,可以用[1:3]选择第二个和第三个元素
X[1, 2] = 9 # 除读取外,我们还可以通过指定索引来将元素写入矩阵
print(X)
节省内存
运行一些操作可能会导致为新结果分配内存。 例如,如果我们用Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
before = id(Y) # Python的id()函数提供了内存中引用对象的确切地址
Y = Y + X
print(id(Y) == before) # 运行Y = Y + X后,我们会发现id(Y)指向另一个位置。
# 这是因为Python首先计算Y + X,为结果分配新的内存,然后使Y指向内存中的这个新位置
# False
# 首先,我们不想总是不必要地分配内存
# 在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。通常情况下,我们希望原地执行这些更新
# 如果我们不原地更新,其他引用仍然会指向旧的内存位置,这样我们的某些代码可能会无意中引用旧的参数
##################################### 执行原地操作 #############################################
# 我们可以使用切片表示法将操作的结果分配给先前分配的数组,
# 例如Y[:] = 。 为了说明这一点,我们首先创建一个新的矩阵Z,其形状与另一个Y相同, 使用zeros_like来分配一个全 0 的块。
Z = torch.zeros_like(Y)
print('id(Z):', id(Z)) # id(Z): 140004761027024
Z[:] = X + Y
print('id(Z):', id(Z)) # id(Z): 140004761027024
before = id(X)
X += Y # 如果在后续计算中没有重复使用X, 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销
print(id(X) == before) # True
转换为其他Python对象
将深度学习框架定义的张量[转换为NumPy张量(ndarray)]很容易,反之也同样容易
torch张量和numpy数组将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
A = X.numpy()
B = torch.tensor(A)
print(type(A), type(B)) #
a = torch.tensor([3.5])
print(a, a.item(), float(a), int(a)) # 要(将大小为1的张量转换为Python标量),我们可以调用item函数或Python的内置函数
# tensor([3.5000]) 3.5 3.5 3
小结
深度学习存储和操作数据的主要接口是张量( N 维数组)。它提供了各种功能,包括基本数学运算、广播、索引、切片、内存节省和转换其他Python对象。
练习
- 将条件语句X == Y更改为X < Y或X > Y,看看得到什么样的张量?
- 用其他形状(例如三维张量)替换广播机制中按元素操作的两个张量。结果是否与预期相同?
练习答案
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(X > Y) # tensor([[False, False, False, False],
# [ True, True, True, True],
# [ True, True, True, True]])
print(X < Y) # tensor([[ True, False, True, False],
# [False, False, False, False],
# [False, False, False, False]])
import torch
a = torch.arange(27).reshape((3, 3, 3))
b = torch.arange(9).reshape((3, 3, 1))
print(a + b) # tensor([[[ 0, 1, 2],
# [ 4, 5, 6],
# [ 8, 9, 10]],
# [[12, 13, 14],
# [16, 17, 18],
# [20, 21, 22]],
# [[24, 25, 26],
# [28, 29, 30],
# [32, 33, 34]]])

