【机器学习】因子分解机(FM) 原理及在召回中的应用(python实现)
FM 原理及在召回中的应用(python实现)
1. 综述
为了学习推荐系统的召回模型，首先梳理了一下FM模型，权当是学习笔记，记录一下。
FM（factor Machine，因子分解机）算法是一种基于矩阵分解的机器学习算法，是为了解决大规模稀疏矩阵中特征组合问题。它是一种通用的预测方法，在即使数据非常稀疏的情况下，依然能估计出可靠的参数进行预测。与传统的简单线性模型不同的是，因子分解机考虑了特征间的交叉，对所有嵌套变量交互进行建模（类似于SVM中的核函数），因此在推荐系统和计算广告领域关注的点击率CTR（click-through rate）和转化率CVR（conversion rate）两项指标上有着良好的表现。此外，FM的模型还具有可以用线性时间来计算，以及能够与许多先进的协同过滤方法（如Bias MF、svd++等）相融合等优点,也被广泛的应用于召回模型中。
本文的主要组织思路如下：
为什么提出FM(演进)
FM具体是什么(原理)
FM模型在召回中的应用
具体怎样应用
2. FM演进
为什么会提出FM模型，下面我从两个角度来简单介绍下FM模型，一个角度是从特征组合模型的进化角度来讲；另外一个角度从协同过滤模型的进化角度来讲。FM模型刚好处于这两类模型进化的交汇口。
特征组合角度
这条路径主要的演进路线是从LR到SVM再到FM模型。LR模型是CTR预估领域早期成功的模型，在深度学习大规模应用之前，大多工业推荐排序系统采取LR这种“线性模型+人工特征组合引入非线性”的模式，具体公式表达如图1所示。因为LR模型具有简单方便易解释容易上规模等诸多好处，所以目前仍然有不少实际系统仍然采取这种模式。但是，LR模型最大的缺陷就是人工特征工程，耗时费力费人力资源，那么能否将特征组合的能力体现在模型层面呢？
image-20211028234308878 图1 LR公式表达为了解决上述的问题，可以直接在图1中的线性公式中直接加入二阶特征组合即可，具体得到图2 所示公式。任意两个特征进行组合，可以将这个组合出的特征看作一个新特征，融入线性模型中。而组合后的特征权重和一阶特征类似可以直接在训练阶段学习得到。其实这种二阶特征组合的使用方式，和多项式核SVM是等价的。虽然这个模型看上去貌似解决了二阶特征组合问题了，但是它有个潜在的问题：它对组合特征建模，泛化能力比较弱。这里举一个例子加深理解，如果设计一个电影评分系统，现在组合特征是用户U对电影M的评分，在数据集合中如果用户张三张三没有评论电影大话西游的记录，如果想要估计张三和大话西游之间，或者说特征分量张三和大话西游之间的相互关系，显然会得到稀疏张三大话西游。即对于观察样本中未出现过交叉的特征分量，不能对相应的参数进行估计。尤其是在大规模稀疏特征存在的场景下，这个毛病尤其突出。比如CTR预估和推荐排序，这些场景的最大特点就是特征的大规模稀疏。所以上述模型并未在工业界广泛采用。那么，有什么办法能够解决这个问题吗？
image-20211028235303494 图2 加入特征组合
于是，FM模型此刻可以闪亮登场了。如图3所示，FM模型也直接引入任意两个特征的二阶特征组合，和SVM模型最大的不同，在于特征组合权重的计算方法。FM对于每个特征，学习一个大小为k的一维向量，于是，两个特征 和的特征组合的权重值，通过特征对应的向量 和的内积$$ 来表示。这本质上是在对特征进行embedding化表征，和目前非常常见的各种实体embedding本质思想是一脉相承的，但是很明显在FM这么做的年代（2010年)，还没有现在能看到的各种眼花缭乱的embedding的形式与概念。所以FM作为特征embedding，可以看作当前深度学习里各种embedding方法的老前辈。当然，FM这种模式有它的前辈模型吗？有，等会会谈。其实，和目前的各种深度DNN排序模型比，它仅仅是少了2层或者3层MLP隐层，用来直接对多阶特征非线性组合建模而已，其它方面基本相同。
image-20211029003500966 图3 fm模型
为什么fm这种通过embedding模式能够解决上述稀疏特征下泛化能力弱的问题？如图3所示，如果和的特征组合在数据集合中没有出现过，在上述SVM模型的特征组合下，是无法学到这个特征组合的权重的。但是FM模型是学习单个特征的embedding,不依赖某个特定的特征组合是否存在，只要该特征在特征组合中出现过，就可以学习他对应的特征组合的embedding向量，于是，尽管这个特征组合没有看到过，但是在预测的时候，如果看到这个新的特征组合，因为和都能学会自己对应的embedding，所以可以通过内积算出这个新特征组合的权重。故而FM泛化能力更强。
协同过滤
协同过滤（Collaborative Filtering，CF）是推荐算法的鼻祖，至今各个互联网公司中，CF都扮演着不可或缺的角色。协同过滤是根据大家的反馈、评论和意见一起对海量的信息进行过滤，从中筛选出目标用户可能感兴趣的信息的推荐过程。大致过程是，将用户与商品放入一个共现矩阵中，矩阵中的值为某用户对某件商品的点击、评价或者购买行为的度量。我们可以将用户感兴趣的所有商品向量化，记为代表该用户的向量，进而可以计算用户间的相似度。于是，可以将与某待推荐用户相似的用户所感兴趣的商品推荐给该用户。类似的，可以将对商品感兴趣的所有用户向量化，记为代表该商品的向量，进而计算物品之间的相似度。在实际的计算过程中，还应该对爆品、高销品与其他商品的相似度进行一定程度上的衰减。相似度的计算也应该进行归一化，排除数量级的影响。
协同过滤的优点是没有显式的学习过程、可解释性强、简单、速度快。其缺点也很明显：协同过滤只考虑了用户和物品的id信息，而无法将用户的属性、物品的属性、上下文考虑在内，无法挖掘用户和物品之间的隐含关系。对于没有购买或者消费的新用户，协同过滤不知如何推荐，泛化性能差，推荐头部效应比较明显。针对这些问题，MF（Matrix Factorization，矩阵分解）模型被提出来。它的核心思想是通过两个低维小矩阵（一个代表用户embedding矩阵，一个代表物品embedding矩阵）的乘积计算，来模拟真实用户点击或评分产生的大的协同信息稀疏矩阵，本质上是编码了用户和物品协同信息的降维模型。当训练完成，每个用户和物品得到对应的低维embedding表达后，如果要预测某个 对 的评分的时候，只要它们做个内积计算$$，这个得分就是预测得分。
本质上，MF模型是FM模型的特例，MF可以被认为是只有User ID 和Item ID这两个特征Fields的FM模型，MF将这两类特征通过矩阵分解，来达到将这两类特征embedding化表达的目的。而FM则可以看作是MF模型的进一步拓展，除了User ID和Item ID这两类特征外，很多其它类型的特征，都可以进一步融入FM模型里，它将所有这些特征转化为embedding低维向量表达，并计算任意两个特征embedding的内积，就是特征组合的权重，如果FM只使用User ID 和Item ID，你套到FM公式里，看看它的预测过程和MF的预测过程一样吗？
在具体的实践过程中，FM模型和MF模型相比，前者继承了后者特征embedding化的特点，同时引入了更多的Side information作为特征，将更多的特征及Side information embedding化融入FM模型中。所以表现的也更加的灵活，能够适应更多的场景。在推荐排序阶段，绝大多数只使用ID信息的模型是不实用的，没有引入Side Information（也就是除了User ID／Item ID外的很多其它可用特征的模型）是不具备实战价值的。原因很简单，大多数真实应用场景中，User/Item有很多信息可用，而协同数据只是其中的一种，引入更多特征明显对于更精准地进行个性化推荐是非常有帮助的。而如果模型不支持更多特征的便捷引入，明显受限严重，很难真正实用，这也是为何矩阵分解类的方法很少看到在排序阶段使用，通常是作为一路召回形式存在的原因。
3. FM原理
FM模型的关键是：特征两两相关。具体的方程式如下：
其中，是第i维特征的隐向量，<-,->代表向量点积，具体表达关系式：
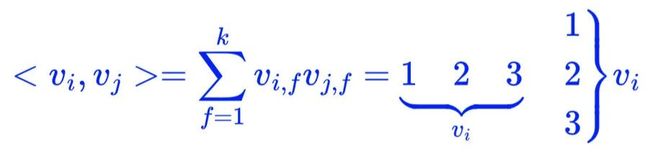image-20211113121414814
其中隐向量的长度为k(k< 第一行到第二行的公式理解可以借助图5所示的直观推理，所要计算的部分就是矩阵的上半角。 至于第二行到第三行提取公共部分理解相对较难，可以借助下图展开公式加以理解，先把k维特征内容抽取到最外层，第一项就剩下 ,然后再按照图6逐层展开合并，可以得到最终结果。 最终的计算等价转化为： 将时间复杂度降低为，即降到线性复杂度，提高了模型的实用性 在网上介绍最多的就是如果利用fm模型的交叉特征的特性提升网络的性能，更好的做分类或者回归任务。对于推荐系统的召回部分，如何通过fm模型计算user和item的相似度，在线上快速获取topK的item？基于上面的基础，下面来探讨一下如何用FM模型在线上做召回。 构建一个线上的召回模块，主要包含四大部分，训练数据的筛选、特征的选择、模型训练，线上服务搭建。数据样本的确认因场景不同而有很大的差异，细节和注意点较多，这里不做讨论，线上服务也不是讨论重点，这个章节主要集中的特征和模型部分。针对一个线上召回系统，可以将特征简化抽样为user特征，item特征，以及context上下文特征（比如用户点外卖所处地址、时间点等）。 为了简化理解，我们可以先考虑只包含user特征和item特征。对于某个用户，我们可以把属于这个用户子集合的特征，查询离线训练好的FM模型对应的特征embedding向量，然后将n个用户子集合的特征embedding向量累加，形成用户兴趣向量U，这个向量维度和每个特征的维度是相同的。类似的，我们也可以把每个物品，其对应的物品子集合的特征，查询离线训练好的FM模型对应的特征embedding向量，然后将m个物品子集合的特征embedding向量累加，形成物品向量I，这个向量维度和每个特征的维度也是是相同的。对于极简版FM召回模型来说，用户兴趣向量U可以离线算好,物品兴趣向量I可以类似离线计算或者近在线计算，问题都不大。 然后将上述计算得到的user embedding 存入线上redis中，线上通过id索引对应的embedding。离线计算的item embedding可以存入Faiss(Facebook开源的embedding高效匹配库)数据库中。通过用户的embedding和Faiss中存储的物料embedding做内积计算，按照得分由高到低返回得分Top K的物料作为召回结果。这样就完成了一个极简版本FM召回模型。但是这个版本的FM召回模型存在两个问题。 问题一：首先我们需要问自己，这种累加用户embedding特征向量以及累加物品embedding特征向量，之后做向量内积。这种算法符合FM模型的原则吗？和常规的FM模型是否等价？ 我们来分析一下。这种做法其实是在做用户特征集合U和物品特征集合I之间两两特征组合，是符合FM的特征组合原则的，考虑下列公式是否等价就可以明白了： 公式(1) 公式(2) 其实两者是等价的，具体推导过程和上节中第三步的推导类似，但是和完全版本的FM比，我们没有考虑U和I特征集合内部任意两个特征的组合。也可以这么思考问题：在上文我们说过，FM为了提升计算效率，对公式进行了改写，改写后的高效计算公式的第一个平方项其实等价于：把所有特征embedding向量逐位累加成一个求和向量V，然后自己和自己做个内积操作 第二个问题是：这个版本FM是个简化版本模型，因为它没考虑场景上下文特征，那么如果再将上下文特征引入，此时应该怎么做呢？ 上下文特征也是很重要的一个特征，它是用户发生行为的场景特征（比如什么时间在什么地方用的什么设备在刷新），这类特征几乎是实时变化的，比如用户上一时刻看了什么电影，下一刻会有历史有很大的相关性，这些动态的特征不太可能离线算好缓存起来。考虑进来上下文特征，如果我们希望构造和标准的FM等价的召回模型，就需要多考虑两个问题：既然部分上下文特征可能是实时变化的，无法离线算好，那么怎么融入上文所述的召回计算框架里？我们需要考虑上下文特征C和用户特征U之间的特征组合，也需要考虑C和物品特征I之间的特征组合。上下文特征有时是非常强的特征。那么，如何做能够将这两对特征组合考虑进来呢？ 首先由于上下文特征的动态性，所以给定用户uid后，可以在线查询或者计算某个上下文特征对应的embedding向量，然后所有上下文向量求和得到综合的上下文向量C。这个过程其实和U及I的累加过程是一样的，区别无非是上下文特征需要在线实时计算。而一般而言，场景上下文特征数都不多，所以在线计算，速度方面应可接受。然后，将U和C向量累加求和，利用（U+C）去Faiss通过内积方式取出Top K物品，这个过程和极简版是一样的，无非查询向量由U换成了（U+C）。通过这种方式取出的物品同时考虑到了用户和物品的特征组合 使用python做二分类任务。数据和代码下载在AI成长社 中回复FM即可 最终的训练结果如下图 使用tensorflow做召回的代码：链接 1.Factorization Machines 2. Factorization Machines 学习笔记 3. 推荐系统召回四模型之：全能的FM模型 4. FM因子分解机的原理、公式推导、python实现和应用 5.深入FFM原理与实战 6.Factorization Machines 7.FM推荐算法中的瑞士军刀 8.从矩阵分解到FM的演进 9.推荐算法中的倚天剑: FM (tensorflow2实现) 本站qq群955171419，加入微信群请扫码：
image-20211109005506337 图4 fm二次项等价化简过程
image-20211109010008253 图5 矩阵直观推理
image-20211113003736335 图6 第三步展开公式
4. 召回的应用
5. 代码实现
import numpy as np
import random
import pandas as pd
from numpy import *
from random import normalvariate # 正态分布
from datetime import datetime
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder
def loadData(base_dir):
'''
load ori_data
Returns: csv_data
'''
movie_columns = ['movie_id', 'title', 'genres']
movies = pd.read_csv(base_dir + "movies.dat", sep='::', header=None, names=movie_columns, engine='python')
rating_columns = ['user_id','movie_id','rating','timestamp']
ratings = pd.read_csv(base_dir + "ratings.dat", sep='::', header=None, names=rating_columns, engine='python')
user_columns = ['user_id','gender','age','occupation','zip']
users = pd.read_csv(base_dir + "users.dat", sep='::', header=None, names=user_columns, engine='python')
data = pd.merge(ratings, movies)
data = pd.merge(data, users)
return data
# 处理数据
def preprocessData(data, ratio):
label = data['rating'].map(lambda x: 1 if x > 3 else -1)
features = ['genres', 'gender', 'age']
data = data[features]
# onehot
data = pd.get_dummies(data)
num = int(data.shape[0] * ratio)
train = data[:num]
train_label = label[:num]
test = data[num:]
test_label = label[num:]
return train, train_label, test, test_label
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
# 训练FM模型
def FM(dataMatrix, classLabels, k, iter, alpha):
'''
:param dataMatrix: 特征矩阵
:param classLabels: 标签矩阵
:param k: v的维数
:param iter: 迭代次数
:return: 常数项w_0, 一阶特征系数w, 二阶交叉特征系数v
'''
# dataMatrix用的是matrix, classLabels是列表
m, n = shape(dataMatrix) # 矩阵的行列数，即样本数m和特征数n
# 初始化参数
w = zeros((n, 1)) # 一阶特征的系数
w_0 = 0 # 常数项
v = normalvariate(0, 0.2) * ones((n, k)) # 即生成辅助向量(n*k)，用来训练二阶交叉特征的系数
for it in range(iter):
for x in range(m): # 随机优化，每次只使用一个样本
# 二阶项的计算
inter_1 = dataMatrix[x] * v # 每个样本(1*n)x(n*k),得到k维向量（FM化简公式大括号内的第一项）
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # 二阶交叉项计算，得到k维向量（FM化简公式大括号内的第二项）
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2. # 二阶交叉项计算完成（FM化简公式的大括号外累加）
p = w_0 + dataMatrix[x] * w + interaction # 计算预测的输出，即FM的全部项之和
tmp = 1 - sigmoid(classLabels[x] * p[0, 0]) # tmp迭代公式的中间变量，便于计算
w_0 = w_0 + alpha * tmp * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] + alpha * tmp * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] + alpha * tmp * classLabels[x] * (
dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
# 计算损失函数的值
if it % 10 == 0:
loss = getLoss(getPrediction(mat(dataMatrix), w_0, w, v), classLabels)
print("第{}次迭代后的损失为{}".format(it, loss))
return w_0, w, v
# 损失函数
def getLoss(predict, classLabels):
m = len(predict)
loss = 0.0
for i in range(m):
loss -= log(sigmoid(predict[i] * classLabels[i]))
return loss
# 预测
def getPrediction(dataMatrix, w_0, w, v):
m = np.shape(dataMatrix)[0]
result = []
for x in range(m):
inter_1 = dataMatrix[x] * v
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # multiply对应元素相乘
# 完成交叉项
interaction = np.sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + dataMatrix[x] * w + interaction # 计算预测的输出
pre = sigmoid(p[0, 0])
result.append(pre)
return result
# 评估预测的准确性
def getAccuracy(predict, classLabels):
m = len(predict)
allItem = 0
error = 0
for i in range(m): # 计算每一个样本的误差
allItem += 1
if float(predict[i]) < 0.5 and classLabels[i] == 1.0:
error += 1
elif float(predict[i]) >= 0.5 and classLabels[i] == -1.0:
error += 1
else:
continue
return float(error) / allItem
if __name__ == '__main__':
data_file = "../data/ml-1m/"
Data = loadData(data_file)
dataTrain, labelTrain, dataTest, labelTest = preprocessData(Data, 0.8)
date_startTrain = datetime.now()
print("开始训练")
w_0, w, v = FM(mat(dataTrain), labelTrain, 4, 100, 0.001)
print("w_0:", w_0)
print("w:", w)
print("v:", v)
predict_train_result = getPrediction(mat(dataTrain), w_0, w, v) # 得到训练的准确性
print("训练准确性为：%f" % (1 - getAccuracy(predict_train_result, labelTrain)))
date_endTrain = datetime.now()
print("训练用时为：%s" % (date_endTrain - date_startTrain))
print("开始测试")
predict_test_result = getPrediction(mat(dataTest), w_0, w, v) # 得到训练的准确性
print("测试准确性为：%f" % (1 - getAccuracy(predict_test_result, labelTest)))
6. 参考
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载黄海广老师《机器学习课程》视频课黄海广老师《机器学习课程》711页完整版课件