【蓝桥杯-筑基篇】排序算法
系列专栏:蓝桥杯
个人主页:个人主页
目录
前言:
一、冒泡排序
二、选择排序
三、插入排序
四、图书推荐
前言:
算法工具推荐:
还在为数据结构发愁吗?这款可视化工具,帮助你更好的了解其数据结构数据结构和算法动态可视化 (Chinese) - VisuAlgo
![]()
一、冒泡排序
1.什么是冒泡排序?
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就象水底下的气泡一样逐渐向 上冒。
思想:
我们要把相邻的元素两两比较,当一个元素大于右侧相邻元素时,交换它们的位置;当一个元素小于右侧相邻元素时,位置不变
动图演示:
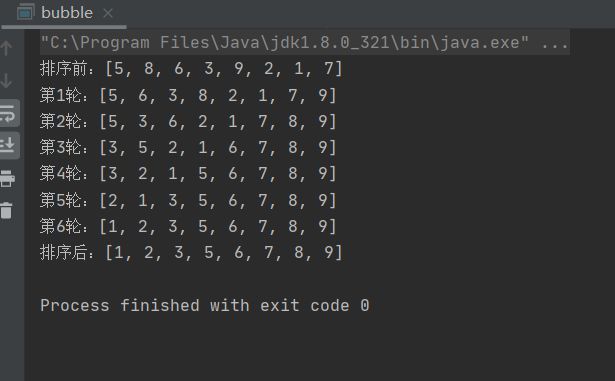
2.冒泡排序代码实现
代码1:
import java.util.Arrays;
public class bubble {
public static void main(String[] args) {
int arr[]={5,8,6,3,9,2,1,7};
System.out.println("排序前:"+Arrays.toString(arr));
BubbleSort(arr);
System.out.println("排序后:"+Arrays.toString(arr));
}
private static void BubbleSort(int[] arr) {
int temp=0; //临时存储变量
int n=0; //统计排序次数
for (int i = 1; i < arr.length; i++) {
n++;
for (int j = 0; j < arr.length-i; j++) {
if (arr[j]>arr[j+1]){
temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
}
}
System.out.println("第"+n+"轮:"+Arrays.toString(arr));
}
}
}
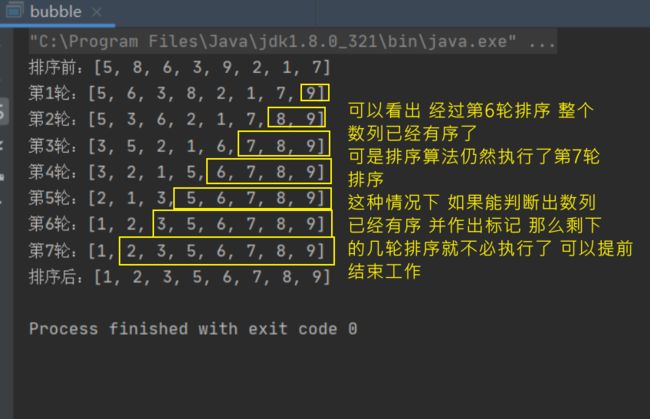
3.冒泡排序代码优化
优化:
因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。
代码2(第一次优化):
import java.util.Arrays;
public class bubble {
public static void main(String[] args) {
int arr[]={5,8,6,3,9,2,1,7};
System.out.println("排序前:"+Arrays.toString(arr));
BubbleSort(arr);
System.out.println("排序后:"+Arrays.toString(arr));
}
private static void BubbleSort(int[] arr) {
int temp=0; //临时存储变量
int n=0; //统计排序次数
for (int i = 1; i < arr.length; i++) {
n++;
boolean flag=true;
for (int j = 0; j < arr.length-i; j++) {
if (arr[j]>arr[j+1]){
temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
flag=false;
}
}
if (flag==true){
break;
}
System.out.println("第"+n+"轮:"+Arrays.toString(arr));
}
}
}与第1版代码相比,第2版代码做了小小的改动,利用布尔变量flag作为标记。如果在本轮排序中,元素有交换,则说明数列无序;如果没有元素交换,则说明数列已然有序,然后直接跳出大循环。
这只是冒泡序优化的第一步,我们还可以进一步来提开它的性能。为了说明问题,这次以一个新的数列为例。
为了说明问题,这次以一个新的数列为例
arr={3,4,2,1,5,6,7,8}
import java.util.Arrays;
public class bubble {
public static void main(String[] args) {
int arr[]={3,4,2,1,5,6,7,8};
System.out.println("排序前:"+Arrays.toString(arr));
BubbleSort(arr);
System.out.println("排序后:"+Arrays.toString(arr));
}
private static void BubbleSort(int[] arr) {
int temp=0; //临时存储变量
int n=0; //统计排序次数
for (int i = 1; i < arr.length; i++) {
n++;
boolean flag=true;
for (int j = 0; j < arr.length-i; j++) {
System.out.println("排序:"+Arrays.toString(arr));
if (arr[j]>arr[j+1]){
temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
flag=false;
}
}
if (flag==true){
break;
}
System.out.println("第"+n+"轮:"+Arrays.toString(arr));
}
}
}
第一轮中:
元素4和5比较,发现4小于5,所以位置不变。
元素5和6比较,发现5小于6,所以位置不变。
元素6和7比较,发现6小于7,所以位置不变。
元素7和8比较,发现7小于8,所以位置不变。
第二轮中:
元素3和4比较,发现3小于4,所以位置不变。
元素4和5比较,发现4小于5,所以位置不变。
元素5和6比较,发现5小于6,所位位置不变。
元素6和7比较,发现6小于7,所以位置不变。
元素7和8比较,发现7小于8,所以位置不变。
.................................................................
按照现有的逻辑,有序区的长度和排序的轮数是相等的。例如第1轮排序过后的有序区长度是1,第2轮排序过后的有序区长度是2....
实际上,数列真正的有序区可能会大于这个长度,如上述例子中在第2轮排序时,后面的5个元素实际上都已经属于有序区了。因此后面的多次元素比较是没有意义的。
那么,该如何避免这种情况呢?我们可以在每一轮排序后, 记录下来最后一次元素交换的位置,该位置即为无序数列的边界,再往后就是有序区了。
4.冒泡排序代码再次优化
代码3:
import java.util.Arrays;
public class bubble {
public static void main(String[] args) {
int arr[]={3,4,2,1,5,6,7,8};
System.out.println("排序前:"+Arrays.toString(arr));
BubbleSort(arr);
System.out.println("排序后:"+Arrays.toString(arr));
}
private static void BubbleSort(int[] arr) {
int temp=0; //临时存储变量
int n=0; //统计排序次数
int lastIndex= 0;//记录最后一次交换的位置
int sortBorder= arr.length-1;//无序数列的边界
for (int i = 1; i < arr.length; i++) {
n++;
boolean flag=true;
for (int j = 0; j < sortBorder; j++) {
System.out.println("排序:"+Arrays.toString(arr));
if (arr[j]>arr[j+1]){
temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
lastIndex=j;
flag=false;
}
}
sortBorder=lastIndex;
if (flag==true){
break;
}
System.out.println("第"+n+"轮:"+Arrays.toString(arr));
}
}
}
二、选择排序
基本介绍:
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。
思想:
选择排序 (select sorting) 也是一种简单的排序方法。它的基本思想是: 第一次从 arr[0]~arr[n-1]中选取最小值,与arr[0]交换,第二次从 ar[1]~arr[n-1]中选取最小值,与 arr[1]交换,第三次从 ar[2]~arr[n-1]中选取最小值,与 arr[2]交换,.................,第 i 次从arr[i-1]~arr[n-1]中选取最小值,与 arr[i-1]交换,.............,第n-1 次从arr[n-2] ~ arr [n-1]中选取最小值,与 arr[n-2]交换,总共通过 n-1 次,得到一个按排序码从小到大排列的有序序列。
1.选择排序
//普通选择排序
public static void sort1(int[] array){
int count = 0;//统计运行次数
int cnt = 0; //交换次数
for(int i=0;iarray[j]) {
min=array[j];
minIndex=j;
}
}
if(minIndex!=i){
cnt++;
array[minIndex]=array[i];
array[i]=min;
}
}
System.out.println(Arrays.toString(array));
System.out.println("运行次数:"+count+"次 交换次数:"+cnt);
} 2.优化版
import java.util.Arrays;
import java.util.Random;
/**
* 选择排序优化
*/
class SelectionSort2 {
public static void main(String[] args) {
//产生一个随机数组
Random r = new Random();
int arr[] = new int[2000];
for(int i=0;i arr[i]) {
minIndex = i;
}
if (arr[maxIndex] < arr[i]) {
maxIndex= i;
}
count++;
}
temp1 = arr[minIndex];
arr[minIndex] = arr[j];
arr[j] = temp1;
if(j!=maxIndex) { //maxIndex不能再原本的minIndex位置上
temp2 = arr[maxIndex];
arr[maxIndex] = arr[arr.length - j - 1];
}else{
temp2 = arr[minIndex];
arr[minIndex] = arr[arr.length - j - 1];
}
arr[arr.length - j - 1] = temp2;
}
//计算算法结束时间
long endStamp = System.currentTimeMillis();
System.out.println("用时总长:"+(endStamp-startStamp));
System.out.println("循环次数:"+count);
System.out.println(Arrays.toString(arr));
}
} 三、插入排序
插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n -1 个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
Java实现插入排序的代码如下:
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}上面的代码使用了两重循环,外层循环枚举未排序部分的元素,内层循环在已排序部分中找到适当的位置并进行插入。
这段代码的时间复杂度为O(n^2),空间复杂度为O(1)。
四、图书推荐
《经典算法的起源》是一本计算机算法方面的科普性书籍,作者以通俗易懂、引人入胜的叙述方式介绍各种算法思想,避免使用一些过于严谨的专业术语。比如,用“大海捞针”来形容一种搜索算法就非常形象,顾名思义,广大读者更容易理解该搜索策略。本书适合对计算机知识有兴趣的初中生、高中生或其他相关人员阅读。计算机专业一、二年级的大学生阅读此书,也会对相关知识的起源有深刻的印象。
本书的目的是向非专业人士介绍算法,使读者理解算法如何运作,而不是阐述算法在生活中的作用。有些书籍在某些方面做了杰出工作,如介绍如何改善大数据的处理,讨论将人工智能和计算设备融入日常生活对人类生存条件的改变。本书对“发生什么”不感兴趣,对“如何发生”感兴趣。为此,本书给出一些真实的算法,不仅描述它们做什么,更重要的是关注它们如何运作。本书将提供详细的解释说明,而非粗略的介绍。
本书由机械工业出版社提供