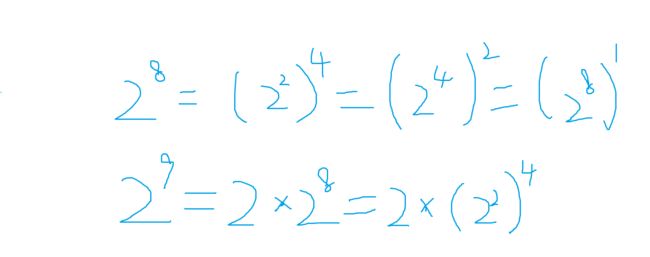【蓝桥杯-筑基篇】分治算法

系列专栏:蓝桥杯

个人主页:个人主页

目录

1.归并排序

2.快速排序

3.幂的相关运算

①API求幂

②幂运算

③分治法

④快速幂

4.二分法

二分查找

---

 

1.归并排序

视频推荐：069_尚硅谷_归并排序算法思路图解_哔哩哔哩_bilibili

对应笔记：归并排序java 

2.快速排序

视频推荐：066_尚硅谷_快速排序算法思路图解_哔哩哔哩_bilibili

对应笔记：快速排序

3.幂的相关运算

①API求幂

Java中求幂可以使用Math.pow()方法，该方法接受两个参数，第一个参数是底数，第二个参数是指数，返回值是底数的指数次幂。例如，要计算2的3次方，可以使用Math.pow(2, 3)方法，返回值为8.

  public static void main(String[] args) {
    	int a=2;
    	int b=3;
      System.out.println(Math.pow(a, b));
    }

②幂运算

这个函数接受两个参数，分别是底数和指数，返回底数的指数次幂。它使用一个循环来计算幂，每次循环将底数乘以自身，共循环 exponent 次。

public static int power(int base, int exponent) {
int result = 1;
for (int i = 0; i < exponent; i++) {
result *= base;
}
return result;
}

③分治法

Java中可以使用Math.pow()方法进行幂运算，但是如果需要使用分治法进行幂运算，可以使用以下代码：

这个函数接受两个参数，分别是底数和指数

	private static int ab2(int a, int b) {
		if(b==0) {
			return 1;
		}
		if(b==1) {
			return a;
		}
		if(b%2==0) {
			return ab2(a,b/2)*ab2(a,b/2);
		}
		else return ab2(a,(b-1)/2)*ab2(a,(b+1)/2);
		
	}

这个方法使用了递归的思想，将幂运算分解成多个小的幂运算，从而减少计算量。

④快速幂

 例如：题目让我们求9的20次方   的最后3位数。

如果用直接用   Math.pow()调用  ，f(x)=a^x ， 随着x单位长度的递增，f(x)会呈“爆炸性”增长。

导致数很大，大到没有任何类型可以承载。

一张纸对折一次，厚度变成原来的2倍。再对折第二次，变为原来的2的2次方倍即4倍。以此类推，假设纸的厚度为0.1mm，则对折24次以后，长度超过1千米；对折39次达55000千米，超过地球赤道长度；对折42次达44万千米，超过地球至月球的距离；对折51次达22亿千米，超过地球至太阳的距离；对折82次为51113光年，超过银河系半径的长度。

我们首先来了解一下“取模”运算的运算法则：

(a + b) % p = (a % p + b % p) % p （1）

(a - b) % p = (a % p - b % p ) % p （2）

(a * b) % p = (a % p * b % p) % p （3）

 所以，我们的代码可以变成这个样子：

public class A {
    public static void main(String[] args) {
    	int a=9;
    	int b=20;
    	
      System.out.println(power(a,b));

    }
    public static int power(int base, int exponent) {
    	int result = 1;
    	for (int i = 1; i <= exponent; i++) {
    	result *= base;
    	result=result%1000;
    	}
    	return result;
    	}



}

优化：扩底 降幂

base=base*base%p;    表示：扩底
exponent=exponent/2;  表示：降幂

 

 

public class A {
    public static void main(String[] args) {
    	int a=9;
    	int b=20;
    	int p=1000;
    	
      System.out.println(power(a,b,p));

    }
    public static int power(int base, int exponent,int p) {
    	int result = 1;
    	while(exponent>0) {
    		if(exponent%2==1) {
    			exponent=exponent-1;
    			result=result*base%p;
    		}
    		base=base*base%p;
    		exponent=exponent/2;
    		
    	}
         return result;

}
}
    

4.二分法

二分和分治都是常见的算法思想，它们的区别在于：

• 二分是一种特殊的分治，即每次将问题分成两个子问题，然后只解决其中一个子问题，另一个子问题则通过递归调用函数来解决。
• 分治是将问题分成多个子问题，然后分别解决每个子问题，最后将子问题的解合并起来得到原问题的解。

二分和分治的区别在于，二分只有两个子问题，而分治可以有多个子问题。此外，二分通常用于解决有序数组的查找问题，而分治则通常用于解决复杂的计算问题，例如排序、矩阵乘法等。

在实际应用中，二分和分治常常结合使用，例如在归并排序中，就使用了分治的思想，而在查找有序数组中的元素时，则使用了二分的思想。

二分查找

二分查找是一种在有序数组中查找某一特定元素的搜索算法。查找过程可以分为以下几个步骤：

1. 首先，确定数组的中间位置 mid。
2. 然后，将要查找的值与数组中间位置的值进行比较。
3. 如果要查找的值等于中间位置的值，则查找成功，返回中间位置的下标。
4. 如果要查找的值小于中间位置的值，则在数组的左半部分继续查找。
5. 如果要查找的值大于中间位置的值，则在数组的右半部分继续查找。
6. 重复上述步骤，直到查找成功或查找失败。

public static int binarySearch(int[] arr, int target) {
    int left = 0, right = arr.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

其中，arr 表示要查找的有序数组，target 表示要查找的值。函数返回要查找的值在数组中的下标，如果没有找到，则返回 -1。

在实际应用中，二分查找的时间复杂度为 O(log n)，比顺序查找的时间复杂度 O(n) 要快得多。因此，当需要在有序数组中查找某一特定元素时，可以考虑使用二分查找算法。