JAVA算法竞赛之搜索图论 思路与案例模板
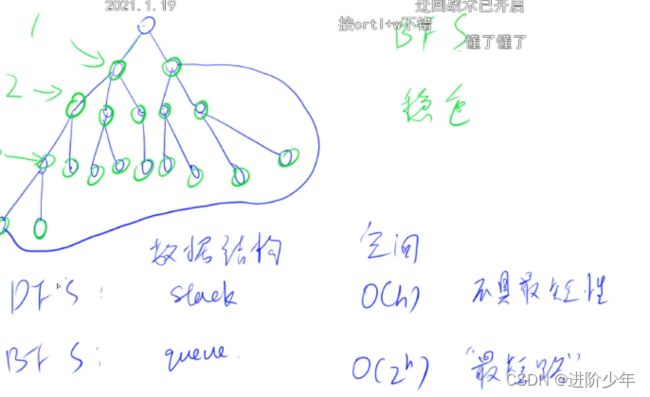
图片来自acwing算法基础课的上课截图可以更好理解这些算法
DFS(回溯+剪枝)
DFS注意顺序
一条路走到黑即选择一个方法一直走到尾部,到尾部之后返回上一个节点判断另一个方案直到本节点可以访问的节点区别访问完毕
桉树型结构来理解的话类似前序遍历
树的前序遍历是指对于树中的每个节点,先访问该节点,然后递归地访问该节点的左子树,再递归地访问该节点的右子树。树的中序遍历是指对于树中的每个节点,先递归地访问该节点的左子树,再访问该节点,最后递归地访问该节点的右子树。树的后序遍历是指对于树中的每个节点,先递归地访问该节点的左子树,再递归地访问该节点的右子树,最后访问该节点。简单来说,前序遍历是根左右,中序遍历是左根右,后序遍历是左右根。这三种遍历的顺序不同,因此它们可以被用来完成不同的任务。例如,在二叉搜索树中,中序遍历可以按照顺序访问树中的所有节点,因此可以用来排序。后序遍历则可以用来计算树中节点的后继和前驱。
经典案例:
给定一个整数 nn,将数字 1∼n1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 nn。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤71≤n≤7
输入样例:
3
输出样例:
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
package ACWing.SearchAndGraphTheory.DFS;
//842. 排列数字
import java.util.ArrayList;
import java.util.Scanner;
public class StaggeredNumerals {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
ArrayList list=new ArrayList<>();
boolean[]arr=new boolean[n+1];
dfs(list,n,arr);
}
public static void dfs(ArrayList list,int n,boolean[]arr){
if(list.size()==n){
for (Integer integer : list) {
System.out.print(integer+" ");
}System.out.println();
return;
}
for (int i = 1; i <= n; i++) {
if (!arr[i]){
list.add(i);
arr[i]=true;
dfs(list,n,arr);
//恢复现场回归到上次的状态
list.remove(list.size()-1);
arr[i]=false;
}
}
}
}
经典8皇后问题
package ACWing.SearchAndGraphTheory.DFS;
//843. n-皇后问题
import java.util.Scanner;
public class NQueensRroblem {
static String[][]arr=new String[20][20];//用截距来判断b=y+x所以有可能是20所以用20
static boolean[]col=new boolean[20];
static boolean[]dg=new boolean[20];
static boolean[]udg=new boolean[20];
static boolean[]row=new boolean[20];
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
arr[i][j]=".";
}
}
//dfs(0,n);
dfs2(0,0,0,n);
}
public static void dfs(int u,int n){
if(u==n){
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(arr[i][j]);
}
System.out.println();
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if(!col[i]&&!dg[u+i]&&!udg[n-u+i]){//精华所在用截距来判断对角线
arr[u][i]="Q";
col[i]=dg[u+i]=udg[n-u+i]=true;
dfs(u+1,n);
col[i]=dg[u+i]=udg[n-u+i]=false;
arr[u][i]=".";
}
}
}
//解法二与上解法的差别在于解法二通过递归遍历了整个节点去判断是否要放皇后解法一是通过循环去判断一整行如何递归到下一行
public static void dfs2(int x,int y,int s,int n){
//设置边界条件
if(y==n){
y=0;
x++;
}
if(x==n){
if(s==n){
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(arr[i][j]);
}
System.out.println();
}
System.out.println();
}return;
}
//不放皇后
dfs2(x,y+1,s,n);
//放皇后
if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[x-y+n]){//条件允许的情况下放皇后
arr[x][y]="Q";
row[x]=col[y]=dg[x+y]=udg[x-y+n]=true;
dfs2(x,y+1,s+1,n);
row[x]=col[y]=dg[x+y]=udg[x-y+n]=false;
arr[x][y]=".";
}
}
}
大体的思路一致没有具体的模板
弹出(边界)条件
进入符合条件的递归
恢复现场
刷题总结:
先判断暴力搜索的情况是否为有顺序的接下去搜索还是全排列,因为时间复杂度不够确定所以尽可能剪枝来缩小查询次数
如果是不按顺序搜索的话一般情况下便是这种模板(全排列)
例题://184. 虫食算 InsectFeedingCalculation
private static boolean dfs(int u) {
if(u==n){
return true;
}
for (int i = 0; i < n; i++) {
if(!st[i]){
path[qu[u]]=i;
st[i]=true;
if(check()&&dfs(u+1)){
return true;
}
path[qu[u]]=-1;
st[i]=false;
}
}
return false;
}
如果是按顺序搜索的话一般便是这种模板(内含有一个遍历的过程必须按照顺序进行遍历组合)即按顺序进行选择来遍历所有的选择情况每种情况之后都必须要恢复现场
例题//187. 导弹防御系统 MissileDefenseSystem
public static void dfs(int[]arr,int su,int sd,int k,int n){
弹出条件
第一种一种情况
第二种情况
.
.
.
}
dfs求组合数类型:
先对要组合的数排序再进行dfs而且必须保证值的不降序性
洛谷例题:
package luogu.dfs;
//P1036 [NOIP2002 普及组] 选数
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Selectron {
static boolean[]st=new boolean[30];
static int n;
static int m;
static int sum=0;
static List set=new ArrayList<>();
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
int[]arr=new int[n];
for (int i = 0; i < n; i++) {
arr[i]=sc.nextInt();
}
Arrays.sort(arr);
dfs(0,0,arr);
int num=0;
for (Integer integer : set) {
if(sushu(integer)){
num++;
}
}
System.out.println(num);
}
public static void dfs(int u,int a,int[]arr){//a和u其实可以合并
if(u==m){
set.add(sum);
return;
}
for (int i = a; i < n; i++) {
if(!st[i]){
sum=sum+arr[i];
st[i]=true;
dfs(u+1,i+1,arr);
sum=sum-arr[i];
st[i]=false;
}
}
}
public static boolean sushu(int a){
for (int i = 2; i < Math.sqrt(a); i++) {
if(a%i==0){
return false;
}
}
return true;
}
}
BFS
按数来理解的话就是依次遍历整层,一层一层遍历,适用与查找最短路径,最短步数等等根据情况使用
将所有一步可以走到的节点全部存到队列中,因为队列的先进先出特性所以必定可以保证先遍历完路径为1的节点才能去遍历2的节点所以保证了到某个点的距离最短
经典迷宫问题
给定一个 n×mn×m 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)(n,m) 处,至少需要移动多少次。
数据保证 (1,1)(1,1) 处和 (n,m)(n,m) 处的数字为 00,且一定至少存在一条通路。
输入格式
第一行包含两个整数 nn 和 mm。
接下来 nn 行,每行包含 mm 个整数(00 或 11),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤1001≤n,m≤100
输入样例:
5 5 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0
输出样例:
8
思路将这一层符合条件的坐标放入队列中,在进入下一层时从队列中取出上一层的坐标进行上下左右的判断以此类推最后遍历到最后一层无法遍历为止
便可以求出这个点到每个点的最短路径(权重相等时是最短路径)
package ACWing.SearchAndGraphTheory.BFS;
//844 走迷宫
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.Scanner;
public class WalkTGHEMaze {
static class Pall{
int x;
int y;
public Pall(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public String toString() {
return "Pall{" +
"x=" + x +
", y=" + y +
'}';
}
}
static Pall[][]palls=new Pall[110][110];//记录路径
static Queue queue=new ArrayDeque<>();
static int[][]d=new int[110][110];
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int[][]arr=new int[n][m];
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < m; j++) {
arr[i][j]=sc.nextInt();
}
}
//初始化距离-1为未被访问过
for (int i = 0; i 0){
Pall t=queue.poll();
for (int i = 0; i < 4; i++) {
int x=t.x+dx[i],y=t.y+dy[i];
if(x>=0&&x=0&&y
例题二
package ACWing.SearchAndGraphTheory.BFS;
//845. 八数码
import java.util.*;
/**
* @author :chenjie
* @date :Created 2022/12/17 13:01
*/
/**
* 本题的总体思路:
* bfs:将所有一步可以走到的节点全部存到队列中,因为队列的先进先出特性所以必定可以保证先遍历完路径为1的节点才能去遍历2的节点所以保证了到某个点的距离最短
* 而本题难点在于如何存储节点的状态和存储节点对应的距离
* 存储节点的状态:题目也有提示1 2 3 x 4 6 7 5 8这样输入便是可以将二维数组压成一维。在进行做题
* 存储节点对应的距离:刚好就对应hashmap类
*/
public class TheEightDigits {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
String s="";
for (int i = 0; i < 9; i++) {
s+=sc.next();
}
System.out.println(s);
System.out.println(bfs(s));
}
public static int bfs(String t){
Queue queue=new ArrayDeque<>();//记录状态
queue.add(t);
Map map=new HashMap<>();//记录对应的步数
map.put(t,0);
int[]dx={1,-1,0,0};
int[]dy={0,0,1,-1};
while (!queue.isEmpty()){
String s = queue.remove();
if("12345678x".equals(s)){
return map.get(s);
}
int n=s.indexOf('x');
int x=n/3;
int y=n%3;
for (int i = 0; i < 4; i++) {
int a=x+dx[i],b=y+dy[i];//遍历上下左右
if(a>=0&&b>=0&&a<3&&b<3){
int l=map.get(s);
String str=swap(s,n,a*3+b);//必须用对象来接副本不然直接用s=的话会出现意外
if(map.containsKey(str)){//如果已经走过来便不在走
continue;
}
map.put(str,l+1);
queue.add(str);
}
}
}
return -1;
}
/**
* setCharAt是精髓所在原本我只能转成char在操作现在可以在字符串上进行修改
* 交换字符串中的俩个字符
* @param s 字符串11
* @param x x的位置下标
* @param x2 交换位的位置下标
* @return
*/
public static String swap(String s,int x,int x2){
StringBuilder str=new StringBuilder(s);
str.setCharAt(x,s.charAt(x2));
str.setCharAt(x2,'x');
return str.toString();
}
}
俩者区别:
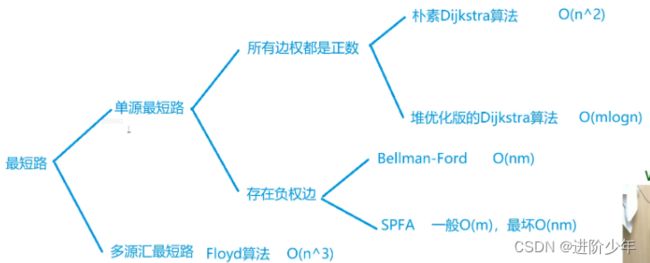
最短路
难点:建图及根据题目构建出响应的模型
对应的使用场景及其时间复杂度
迪杰斯特拉算法:(基于贪心算法)
从未访问的点中找出当前与我最短距离的点并更新这个点到其他点的距离选取最小值来进行存储,所以最后到n点肯定是最短的距离
朴素方法:
package ACWing.SearchAndGraphTheory.最短路;
//849. Dijkstra求最短路 I 朴素版的适用与稠密图即边比点大的多
import java.util.Arrays;
import java.util.Scanner;
/**
* 贪心思想
* 从未访问的点中找出当前与我最短距离的点并更新这个点到其他点的距离选取最小值来进行存储,所以最后到n点肯定是最短的距离
*/
public class Dijkstra1 {
static int n,m;
static int[][]arr=new int[510][510];
static int[]dist=new int[510];
static boolean[]st=new boolean[510];
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
for (int i = 0; i < n; i++) {
Arrays.fill(arr[i],(int)1E9);
}
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int t=sc.nextInt();
arr[a][b]=Math.min(arr[a][b],t);
}
System.out.println(dijkstra());
}
//模板开始处
public static int dijkstra(){
Arrays.fill(dist,(int)1E9);
dist[1]=0;
for (int i = 0; i < n; i++) {
int t=-1;
for (int j = 1; j <= n; j++) {
if(!st[j]&&(t==-1||dist[t]>dist[j])){
t=j;
}
}
st[t]=true;
for (int j = 1; j <= n; j++) {
dist[j]=Math.min(dist[j],arr[t][j]+dist[t]);
}
}
if(dist[n]==(int)1E9){
return -1;
}
return dist[n];
}
}
堆优化法(稀疏图)
这里的堆优化就是利用堆(优先队列)的特点会将最小权值点存储在队头这样便可以不需要去通过遍历邻接表的权值信息来实现查找最小值。
package ACWing.SearchAndGraphTheory.最短路;
//850. Dijkstra求最短路 II
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
//堆优化及可以用堆的特性可以找出当前权值最小的一个节点
public class Dijkstra2 {
static int n , m , N = 1000010;
static PriorityQueue q = new PriorityQueue<>((a, b)->{return a[1] - b[1];});//堆定义排序规则
static int[] dist = new int[N];//距离数组
static boolean[] f = new boolean[N];//标记数组
static int[] h = new int[N], ne = new int[N], e = new int[N], w = new int[N];//邻接表
static int idx ;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
Arrays.fill(h,-1);
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
add(a,b,c);
}
System.out.println(Dijkstra());
}
static int Dijkstra(){
Arrays.fill(dist,0x3f3f3f3f);//初始化数组使其达到无穷大
dist[1]=0;
q.offer(new int[]{1,0});//初始化堆中的元素
while (q.size()!=0){//类似与bfs
int[] poll = q.poll();
int t=poll[0];
int distmin=poll[1];
if(f[t]){
continue;
}
f[t]=true;
for (int i = h[t]; i != -1; i=ne[i]) {
int j=e[i];
if(dist[j]>distmin+w[i]){//如果存储的距离大小大于本节点到j节点的距离的话更新
dist[j]=distmin+w[i];
q.offer(new int[]{j,dist[j]});//将这个节点存储进去排序
}
}
}
if(dist[n]==0x3f3f3f3f){
return -1;
}else {
return dist[n];
}
}
public static void add(int a,int b,int c){
e[idx]=b;
ne[idx]=h[a];
w[idx]=c;//存储到b的权值
h[a]=idx++;
}
}
bellman-ford(可处理负权边)
查询存在负权值的边而且不得走超过k条边而到达目的地的题
思想为不断更新本节点的最短距离循环k次便是从1走了k条路径因为一次时dist被更新成上一个点到这个点的最短距离第二遍历时dist[a]就是其他点到这个点的最短距离用这个a去更新b便是从a的上一个节点走到了b的最短距离,因此循环k次便是1到n经过不超过k条路径的最短距离
模板/案例:
package ACWing.SearchAndGraphTheory.最短路;
//853. 有边数限制的最短路
import java.util.Arrays;
import java.util.Scanner;
public class BellmanFord {
static int[]dist=new int[510];
static int[]backup=new int[510];
static int n,m,k;
static class Edge{
int a;
int b;
int w;
public Edge(int a, int b, int w) {
this.a = a;
this.b = b;
this.w = w;
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
k=sc.nextInt();
Edge[]edges=new Edge[510];
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int w=sc.nextInt();
edges[i]=new Edge(a,b,w);
}
bellman_ford(edges);
if(dist[n]>0x3f3f3f3f/2){//除二的意义在于负权边可能会导致走不到的点被更新成小于0x3f3f3f3f的数所以小于0x3f3f3f3f/2可以更好判断是否走的到
System.out.println("impossible");
return;
}
System.out.println(dist[n]);
}
//模板处
public static void bellman_ford(Edge[] edges){
Arrays.fill(dist,0x3f3f3f3f);
dist[1]=0;
for (int i = 0; i < k; i++) {
backup= Arrays.copyOf(dist, 510);//防止联代更新b点的距离及a刚刚更新过就作为起始点去更新b导致不是走少于k条路径这个条件
for (int j = 0; j < m; j++) {
int a=edges[j].a,b=edges[j].b,w=edges[j].w;
dist[b]=Math.min(dist[b],backup[a]+w);
}
}
}
}
spfa(可处理负权边)
思想:
利用栈来实现不断的更新相接的边来实现连环的更新与遍历有着相同的作用
模板:
static int spfa(){
Arrays.fill(dist,0x3f3f3f3f);
Queuequeue=new ArrayDeque<>();
queue.add(1);
st[1]=true;
dist[1]=0;
while (!queue.isEmpty()){
int remove = queue.remove();
st[remove]=false;
for (int i = h[remove]; i !=-1; i=ne[i]) {
int j=e[i];
if(dist[j]>dist[remove]+w[i]){
dist[j]=dist[remove]+w[i];
if(!st[j]){
queue.add(j);
st[j]=true;
}
}
}
}
return dist[n];
}
判断负环:
记录走的步数就好了如果大于n就一定存在一个点走了俩次又因为是负的所以才能走所以是负环
//851. spfa求最短路
import java.util.*;
public class Main {
static int n , m , N = 1000010;
static int[] dist = new int[N];//距离数组
static int[] cnt=new int[1000010];
static boolean[] st = new boolean[N];//标记数组
static int[] h = new int[N], ne = new int[N], e = new int[N], w = new int[N];//邻接表
static int idx ;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
Arrays.fill(h,-1);
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
add(a,b,c);
}
if(spfa()){
System.out.println("Yes");
}else{
System.out.println("No");
}
}
static boolean spfa(){
Queuequeue=new ArrayDeque<>();
for(int i=1;i<=n;i++){
queue.add(i);
st[i]=true;
}
while (!queue.isEmpty()){
int remove = queue.remove();
st[remove]=false;
for (int i = h[remove]; i !=-1; i=ne[i]) {
int j=e[i];
if(dist[j]>dist[remove]+w[i]){
dist[j]=dist[remove]+w[i];
cnt[j]=cnt[remove]+1;
if(cnt[j]>=n){
return true;
}
if(!st[j]){
queue.add(j);
st[j]=true;
}
}
}
}
return false;
}
public static void add(int a,int b,int c){
e[idx]=b;
ne[idx]=h[a];
w[idx]=c;//存储到b的权值
h[a]=idx++;
}
}
Floyed(多源多汇最短路问题)
利用邻接矩阵来存储图
基于动态规划
状态转移方程: distj=Math.min(distj,distj+disti);将一条路径拆分成俩条路径的和这样只要俩条路径被更新过那便可以去更新一整条路径
利用中间点来优化掉所有路径的最小值实现每个点到另一个点的距离最小
模板:
package ACWing.SearchAndGraphTheory.最短路;
//854. Floyd求最短路
import java.util.Scanner;
public class Floyd {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int k=sc.nextInt();
int[][]dist=new int[n+1][n+1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if(i==j){
dist[i][j]=0;
}else {
dist[i][j]=(int)1E9;
}
}
}
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
dist[a][b]=Math.min(dist[a][b],c);
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int l = 1; l <=n ; l++) {
dist[j][l]=Math.min(dist[j][l],dist[j][i]+dist[i][l]);
}
}
}
for (int i = 0; i < k; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
if(dist[a][b]<(int)1E9/2){
System.out.println(dist[a][b]);
}else {
System.out.println("impossible");
}
}
}
}
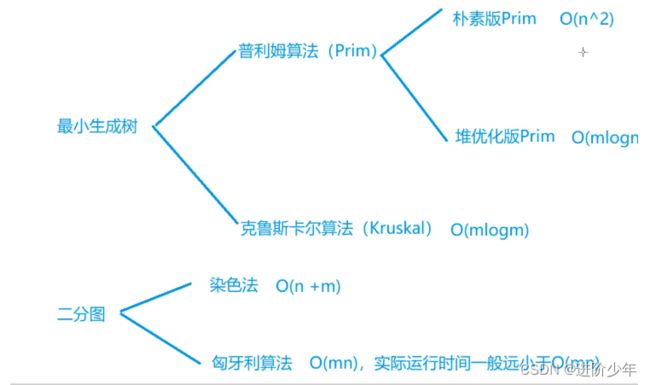
最小生成树
pirm最小生成树算法(On^2)
与迪杰斯特拉极度相似
迪杰斯特拉是查找未在集合中的距离源点最近的节点去更新未在集合中的点到源点的距离
prim算法是查找未在集合中的距离集合最近的节点去更新未在集合中的点到整个集合的距离
俩个距离最短的差别:虽然这两个算法在添加新结点时,都是选择“距离最短”的结点加入集合,但是Prim算法中,“距离最短”是指未访问的结点到已经访问的所有结点距离最小,即将已经访问的结点视为一个整体,将距离最小的结点加入到已访问的集合中;而在Dijkstra算法中,“距离最短”是指所有未访问结点(通过已访问的结点)到源点距离最小。
package ACWing.SearchAndGraphTheory.最小生成树;
//858. Prim算法求最小生成树
import java.util.Arrays;
import java.util.Scanner;
public class Prim {
static int sum;
static int n,m;
static int[]dist=new int[510];//代表着这个点到集合的距离把已访问过的节点看成一个集合
static boolean[]st=new boolean[510];//代表进入了集合
static int[][]arr=new int[510][510];
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
for (int i = 0; i <= n; i++) {
Arrays.fill(arr[i],0x3f3f3f3f);
}
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
arr[a][b]=Math.min(arr[a][b],c);
arr[b][a]=Math.min(arr[b][a],c);
}
prim();
if(sum==0x3f3f3f3f){
System.out.println("impossible");
}else {
System.out.println(sum);
}
}
static void prim(){
Arrays.fill(dist,0x3f3f3f3f);
for (int i = 0; i < n; i++) {
int t=-1;
for (int j = 1; j <= n; j++) {
if(!st[j]&&(t==-1||dist[t]>dist[j])){//确保t=j至少执行一次
t=j;
}
}
if(i!=0&&dist[t]==0x3f3f3f3f){
sum=0x3f3f3f3f;
return;
}
if(i>0){
sum=sum+dist[t];//提前相加防止出现负权值的自环将本身更新了最小生成树不能有自环
}
for (int j = 1; j <= n; j++) {
dist[j]=Math.min(dist[j],arr[t][j]);
}
st[t]=true;
}
}
}
Kruskal (Omlogm)
思路:
就是并查集的思路,先按权值从小到大排序然后对他进行并查集操作,如果俩个点所属的集合不同就说明这俩个点还没被访问过所以进行并查集操作将俩个点合并起来成为一个集合因为排序过所以一定是小的先被访问到就与上方prim算法的查找最小值一致了,再一个就是修改了他们的父节点使其成为一个集合这样便可以无视重边,当重复遍历到这俩个点的时候因为已经是一个集合的点了就跳过
模板的重点在于并查集查询find,class的自定义排序
package ACWing.SearchAndGraphTheory.最短路;
//859. Kruskal算法求最小生成树
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
//类似并查集合并操作去添加集合
public class Kruskal{
static int N=100010;
static int[]p=new int[N];
static class Pall{
int x;
int y;
int l;
public Pall(int x, int y, int l) {
this.x = x;
this.y = y;
this.l = l;
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
Pall[]palls=new Pall[m];
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
palls[i]=new Pall(a,b,c);
}
Arrays.sort(palls,cmp);
for (int i = 1; i <= n; i++) {
p[i]=i;
}
int sum=0,num=0;
for (int i = 0; i < m; i++) {
int a=palls[i].x;
int b=palls[i].y;
a=find(a);
b=find(b);
if(a!=b){
p[a]=b;
sum=sum+palls[i].l;
num++;
}
}
if(num cmp=new Comparator()
{
@Override
public int compare(Pall o1, Pall o2) {
return o1.l-o2.l;
}
//将两边的权值按照从小到大排序
};
}
二分图
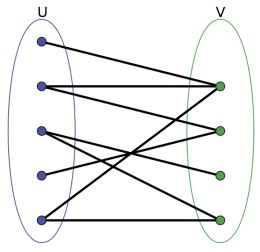
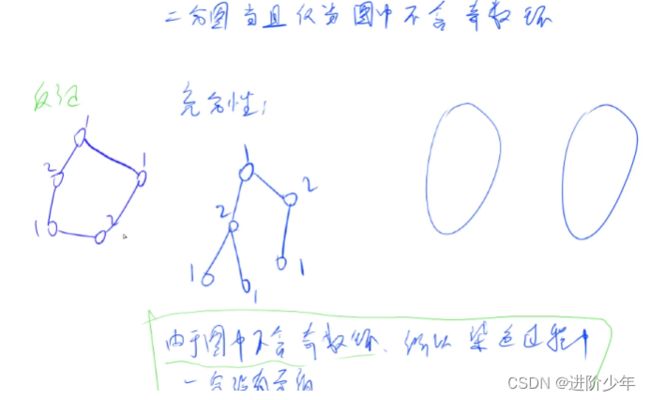
二分图定义:
-
二分图又称为二部图,如果一个点集可以被分成两个部分,所有的边都在这两个部分之间,而每个集合内部没有边,则称这个图是一个二分图。如下图:
集合内部没有边。
显然(哈哈),如果一个图是二分图,则其去掉一些边之后还是二分图。
下面证明一个重要的定理:一个图是二分图 ⟺图中不存在奇数环 (存在奇数环的话集合中必定存在边就矛盾了) ⟺ 染色过程中不存在矛盾
首先证明:图中不存在奇数环 ⟺ 染色过程中不存在矛盾
染色法判断二分图
一个二分图确定一个点的颜色便可以确定所有点的颜色
因此如果知道一条边存在同样的颜色便可以确定他不是二分图
模板:
package ACWing.SearchAndGraphTheory.二分图;
//860. 染色法判定二分图
import java.util.Arrays;
import java.util.Scanner;
public class DichotomousGraphDeterminedStainingMethod {
static int n,m,idx;
static int[]h=new int[100010];
static int[]e=new int[100010];
static int[]ne=new int[100010];
static int[]color=new int[100010];
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
Arrays.fill(h,-1);
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
add(a,b);
add(b,a);
}
for (int i = 1; i <= n; i++) {
if(color[i]==0){//防止有不想连的连通块及俩个图没有相较的情况
if(!dfs(i,1)){
System.out.println("No");
return;
}
}
}
System.out.println("Yes");
}
public static void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
public static boolean dfs(int u,int c){//根据dfs去遍历所有的相连边使其染色
color[u]=c;//染色
for (int i = h[u]; i !=-1; i=ne[i]) {
int j=e[i];
if(color[j]==0){
if (!dfs(j,3-c)) {//精髓处理2 1反复使用
return false;
}
}else if(color[j]==c){//我的子节点与我出现相同的颜色便矛盾了
return false;
}
}
return true;
}
}
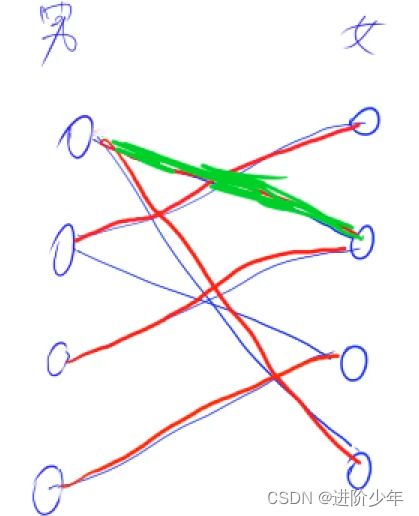
匈牙利算法
思路:
选定一个集合去匹配了一个集合的相连点,如果另一个集合中与我连线的点已经被匹配走了那就去访问将他匹配的点查看是否还可以匹配别的点是否可以将已匹配的点让出来如果可以就将已匹配的点让出来去匹配另一个未被匹配的点,将之前匹配的点让给别人以此实现最大匹配
模板:
package ACWing.SearchAndGraphTheory.二分图;
//匈牙利算法 861. 二分图的最大匹配
import java.util.Arrays;
import java.util.Scanner;
public class Hungary {
static int N=510,M=100010;
static int[]e=new int[M];
static int[]ne=new int[M];
static int[]h=new int[N];
static int n,m,idx;
static int[]match=new int[N];//记录右半边所匹配的点的位置
static boolean[]st=new boolean[N];//防止多条匹配
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n1=sc.nextInt();
n=sc.nextInt();
m=sc.nextInt();
Arrays.fill(h,-1);
for (int i = 0; i < m; i++) {
int a=sc.nextInt();
int b=sc.nextInt();
add(a,b);
}
int res=0;
for (int i = 1; i <= n1; i++) {
Arrays.fill(st,false);
if(find(i)){//本节点可以匹配就可以加一
res++;
}
}
System.out.println(res);
}
public static void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
public static boolean find(int x){
for (int i = h[x]; i !=-1; i=ne[i]) {
int j=e[i];
if(!st[j]){
st[j]=true;
if(match[j]==0||find(match[j])){//如果这个点未被匹配或者匹配者可以有其他没有访问的点了可以访问就对这个点的匹配对象进行修改
match[j]=x;
return true;
}
}
}
return false;
}
}
图论刷题总结: