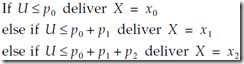计算统计-Chap4 生成随机变量 （1）通用技术

许多计算统计方法需要从已知概率分布中生成随机变量，这也是用于统计推断（statistical inference)的蒙特卡罗方法的核心。

1.均匀随机数（Uniform Random Numbers）

均匀分布在(0,1)上的随机数是生成其它随机变量的基础。目前，计算机依靠判决算法生成的其实是伪随机数。生成均匀随机变量的相关方法在[Gentle, 1998]中有详尽的讨论。

 

生成均匀分布随机变量的matlab函数是rand，其语法如下

1）rand(m,n)：生成m*n的均匀随机矩阵

2）rand(n)：生成n*n的均匀随机矩阵

该函数生成的随机数序列依赖于生成器的种子（或状态）

1）rand(‘state’,0)：生成器设为初始状态

2）rand('state',j)：生成器设为地j个状态

3）S = rand(‘state’)：获取当前状态，s是35维的向量

 

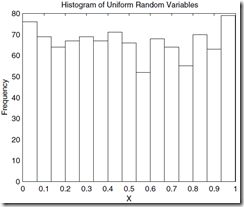
例：绘制均匀分布随机变量的直方图

% Obtain a vector of uniform random variables in (0,1).

x = rand(1,1000);

% Do a histogram to plot.

% First get the height of the bars.

[N,X] = hist(x,15);

% Use the bar function to plot.

bar(X,N,1,'w')

title('Histogram of Uniform Random Variables')

xlabel('X')

ylabel('Frequency')

2.逆变化法（Inverse Transform Method）

逆变化法可用从连续分布中生成随机变量，它利用累计分布函数（CDF，cumulative distribution function）是(0,1)上的均匀分布[Ross, 1997]：若U是uniform(0,1)随机变量，那么可通过 获得需要的随机变量。该方法的通用流程如下：

1）推导逆分布函数

2）生成均匀随机数

3）从 获得需要的随机变量X

 

该方法也可扩展到离散情况[Banks, 2001，流程如下：

1）定义概率质量函数（PMF，probability mass function），。注意k可能无限增长

2）生成均匀随机数

3）通过 ，获得随机变量X

   

   

 

 

例：生成离散随机变量

假设其概率质量函数为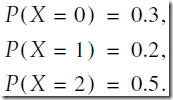 ，则累计分布函数为 ，生成随机变量X的原则为 ，代码如下

% Set up storage space for the variables.

X = zeros(1,100);

% These are the x's in the domain.

x = 0:2;

% These are the probability masses.

pr = [0.3 0.2 0.5];

% Generate 100 rv’s from the desired distribution.

for i = 1:100

  u = rand; % Generate the U.

  if u <= pr(1)

    X(i) = x(1);

  elseif u <= sum(pr(1:2))

    % It has to be between 0.3 and 0.5.

    X(i) = x(2);

  else

    X(i) = x(3); % It has to be between 0.5 and 1.

  end

end

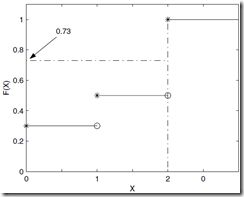
下图说明了利用你变化法生成离散随机变量的过程：当生成均匀随机数u=0.73时，相应生成随机变量x=2，如虚线所示。

3.接受-拒绝 方法(Acceptance-Rejection Method)

某些情况下，有简单方法可以从概率密度g(y)中生成随机变量。那么，可以利用这个密度来生成我们需要的概率密度f(x)，方法是从g(y)中生成随机数Y，并且以正比f(x)/g(y)的概率接受这个生成的数值，流程如下：

1）选择容易抽样的密度g(y)

2）找到常数c，保证

3）从g(y)生成随机数Y

4）从均匀分布中生成随机数U

5）若 ，则接受X＝Y，否则进入第3 步

 

例：生成beta(2,1)分布

带入的此分布的概率密度函数为

1）由于此概率密度定义域为(0,1)，因而选择g(y)为均匀分布，g(y)＝1，0<x<1

2）f(x)/g(y)最大值为2，因此取常数C=2

c = 2; % constant

n = 100; % Generate 100 random variables.

% Set up the arrays to store variates.

x = zeros(1,n); % random variates

xy = zeros(1,n);% corresponding y values

rej = zeros(1,n);% rejected variates

rejy = zeros(1,n); % corresponding y values

irv = 1;

irej = 1;

while irv <= n

  y = rand(1); % random number from g(y)

  u = rand(1); % random number for comparison

  if u <= 2*y/c;

    x(irv) = y;

    xy(irv) = u*c;

    irv = irv+1

  else

    rej(irej) = y;

    rejy(irej) = u*c; % really comparing u*c<=2*y

    irej = irej + 1

  end

end

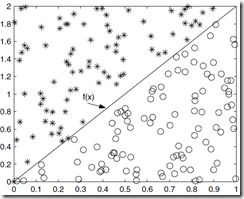
下图说明接受的变量值位于曲线f(x)下方