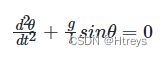数字孪生示范项目——从单摆谈起(1)
谈到数字孪生,相信大家都不感到陌生,举几个离我们很近的例子吧:当你戴上一个特殊手套,弯曲手指或者攥紧拳头时,一只机械臂也会跟你做出相同的动作。还有当今特别火热的元宇宙,我们构造出来的虚拟人,能够仿照我们讲话、做手势等等。
而我最近在做的项目,其背后逻辑也是数字孪生,也就是make sense digital twins.
数字孪生项目1
先放个视频在这里看一下我要做的单摆大致是个什么东西,大致能达到什么效果。我所做的与之相似,我是利用物理中的单摆,在单摆上绑上一个传感器,用于抓捕数据来获取单摆目前所在位置,利用传感器中抓捕出来的数据,在计算机中绘制出一个反映单摆位置的图像,拿这个图像跟实际的单摆进行对比,达到同步的效果,也就是上述视频里的那样。
用到的传感器就是上篇文章里介绍到的Waffle Nano——一块OpenHarmony2.0的海思芯片Python开发板。
idea有了,话不多说开始动手。
先从某宝上买到了单摆的模型,用于研究其运动规律。收到包裹打开安装完成后,试验了几次,发现效果还不错,于是开始动手写项目方案。
单摆模型大致组装好了,下一步我先研究利用角加速度、角速度读取数据,拿waffle nano先抓几组数据测测看,顺便推进算法的编写,还是先采用把waffle nano绑到物块上的方法搞装置,外接供电电池已经充上电了,下一步我先把抓什么数据和算法搞好,再考虑WiFi传数据和电脑端绘制图像的问题
(图为当时设计的方案)
想法固然是好,但是理论就是得结合实际啊。
虽然想法设计的是挺好的,但是手头的这个单摆模型并不像是初中高中所学到的那样,在一个二维平面内有规律的摆动,而是三维的摆动,且因受空气阻力及及其他因素的影响,随着时间的推移摆动幅度越来越小,逐渐停了下来,更甚者,小球由于还要受地转偏向力的作用,摆的形态会越来越歪。这仿佛是给我幼小的心灵蒙上了一层阴霾。原来之前学到的理论知识放到实际生活里还是有很多干扰因素,跟理想情景还是存在蛮多偏差的。。。
单摆实验,摆球的质量需要比较大,摆线必须是轻质不可伸长的,质量越小越好。摆线的长度需要比较长,一般在米这个量级。摆线越长,越轻,摆球越重,单摆实验的实验误差就会越小。 —— by 互联网
上网查阅资料得知,误差是固然存在的,我只能通过不断改进装置来减小误差。
正当我冥思苦想之际,同实验室的学长给出了一个很好的建议:
考虑到地转偏向力的影响,小球摆着摆着会碰到底座上的杆子,不如把一根绳吊着的小球改成亚克力长条+轴承结构
这无疑是一个很棒的idea,看来虽然我年龄不小,思维却固化了(其实是学长接触的机械结构比较多,遇到情况能一针见血地指出问题所在)
与此同时,我也想到了一个方案,把传感器Waffle Nano制作成一个大球,里面塞好配重,让绳子重一些,这样就能把实验误差减小一部分。
这时导师说,先搞IoT,先把算法模型写出来,也就是利用电脑上的编程软件,不根据现实情况,利用单摆的公式,去建立起一个展现在电脑屏幕上的二维模型,原理可能跟现在的“数学建模”比较类似。我上网查阅了单摆的相关公式:(感谢度娘)
决定设计一个微分方程来绘制单摆轨迹。
用到的方程如下:
于是经过设计和参考Github上的一些demo @skyerhxx 等人,首先设计出了一个纯数学算法:
首先先导入必要的库
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import math
import matplotlib.animation as animation然后是设计微分方程,
dtheta1_dt表示theta对t的一阶导数
dtheta2_dt表示theta对t的二阶导数
def mode1(theta,t,g,l):
theta1 = theta[0]
theta2 = theta[1]
dtheta1_dt = theta2
dtheta2_dt = - (g/l)*math.sin(theta1)
dtheta_dt = [dtheta1_dt, dtheta2_dt]
return dtheta_dt然后后面是我们可以自己根据实际情况来写的量以及定义了一些初始量:绳长l和当地重力加速度g
g=9.8
l=1
theta_0 = [0,3] #theta初值
t = np.linspace(0,10,150)然后是利用常微分方程求解
#solving 常微分方程
theta = odeint(mode1,theta_0,t,args = (g,l))最后利用Artistanimation生成gif动画:
fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(1, 1, 1,facecolor='black')
plt.rcParams['font.size'] = 15
ims = [] #将每一帧都存进去
for i in range(len(theta)):
ln, = ax.plot([0, np.sin(theta[i, 0])], [0, -np.cos(theta[i, 0])], color='white', lw=2)
bob, = ax.plot(np.sin(theta[i, 0]), -np.cos(theta[i, 0]),'o',markersize=20,color='yellow')
tm = ax.text(-0.9, 0.25, 'Time = %.1fs' % t[i])
ims.append([ln, bob, tm])
ax.set_aspect('equal', 'datalim')
#ax.set_aspect('equal')
ani = animation.ArtistAnimation(fig, ims, interval=50) #生成动画
#保存成gif
ani.save("单摆.gif", writer='pillow')
最终实现了单摆的数学模型。(未完待续)