计算机图形学实验二——二维图形几何变换及裁剪

【实验名称】 二维图形几何变换及裁剪
【实验目的】
1． 通过实验，进一步理解和掌握二维几何图形的基本变换及复合变换的原理；
2． 理解和掌握cohen-sutherland裁剪算法的基本思想。
【实验原理】
1．平移变换、旋转变换、比例变换、对称变换的变换矩阵；
绕任意点旋转、相对任意点缩放的变换矩阵；
相对于任意参考点(xF,yF)的二维几何变换,基本思路是，将图形经过平移，使参考点与原点重合，此时相对于参考点的变换变成相对于原点的基本几何变换，最后再平移，使参考点回到原来的位置。
（1）相对于(xF,yF)点的比例变换，变换矩阵如下：

(2) 相对于(xF,yF)点的旋转变换，变换矩阵如下：

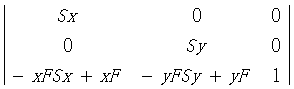
2．Cohen-Sutherland端点编码算法
（1）若线段P1P2两端点的四位编码均为0,则两端点均在窗口内,该线段完全可见,显示该线段,算法结束;
(2) 若线段P1P2两端点的四位编码按位“与”结果为非0,则该线段完全不可见,算法结束。
(3)若线段两端点的四位编码按位“与”结果为0, 找到P1P2在窗口外的一个端点P1(或P2),用窗口相应的边与P1P2的交点取代该端点P1（或P2）, 返回(1)步。
【实验内容】
1．显示一个飞机：（飞机各顶点的坐标存放在数组中）
(1)按比例缩小或放大.缩放比例由键盘输入，缩放的参考点由用户确定；

#include 
#include 
#include 
#include 
//f[20][2]中存放的是飞机的关键点
Int f[15][2] = 
{285,70,310,100,310,185,430,240,440,260,310,225,310,355,345,400,225,400,260,355,260,225,130,260,140,240,260,185,260,100};
int b;
float k;
int n = 15;
int a[15][2];
void DDALine( int x0,int y0,int x1,int y1 )
{
    //DDA画直线算法
	int dx,dy,epsl,k;
	float x,y,xIncre,yIncre;
	dx = x1 - x0;
	dy = y1 - y0;
	x = x0;
	y = y0;
	if( abs(dx) > abs(dy) )
        epsl = abs(dx);
    else
        epsl = abs(dy);
	xIncre = (float)dx / (float)epsl;
	yIncre = (float)dy / (float)epsl;
	for( k = 0; k <= epsl; k++ )
	{
		putpixel((int)(x+0.5),(int)(y+0.5),GREEN);
		x += xIncre;
		y += yIncre;
	}
 
}
void Draw()
{
	int i,j,p,q;
	int gdriver = DETECT,gmode;
    printf("请输入参考点(X,Y):\n");
	scanf("%d %d",&p,&q);
	printf( "请输入放大倍数(缩小0.5倍也是可以的)：" );
	scanf( "%f",&k );
    for( i = 0; i < n; i++ )
	{
	    //a[i][0]中存的是x
	    //a[i][1]中存的是y
	    a[i][0] = ((f[i][0] - p) * k) + p;
	    a[i][1] = ((f[i][1] - q) * k) + q;
    }
	initgraph( 960,540 );
	for( j = 0; j < 1000; j++ )
		for( i = 0; i < 1000; i++ )
            putpixel( i,j,WHITE );//首先生成一个960*540大小的窗口，并置成白色
	for( i = 0; i < n - 1; i++ )
        //DDA画直线，首先将飞机的点顺时针按序连成线
		DDALine( a[i][0],a[i][1],a[i+1][0],a[i+1][1] );
	DDALine( a[0][0],a[0][1],a[n-1][0],a[n-1][1] );
}

void change()
{
	int i,j,k,s,dx,dy,temp;
	int x0,y0,x1,y1,x2,y2;
	for( i = 0; i < n; i++ )
	{
		if( i == n - 1 )
		{
			x0 = a[i][0];
			y0 = a[i][1];
			x1 = a[0][0];
			y1 = a[0][1];
		}
		else
		{
			x0 = a[i][0];
			y0 = a[i][1];
			x1 = a[i+1][0];
			y1 = a[i+1][1];
		}
		dx = x0 - x1;
		dy = y0 - y1;
		if( y0 > y1 )
		{
			temp = x0;
              x0 = x1;
			  x1 = temp;
            temp = y0;
			  y0 = y1;
			  y1 = temp;
		}
		for( j = y0; j < y1; j++ )
		{
			s = int( (j - y0) * dx / dy ) + x0;//求交点坐标
			for( k = s; k < 1000; k++ )
			{
					if( getpixel( k,j ) == WHITE )
                        putpixel( k,j,BLACK);
					else if( getpixel(k,j) == BLACK)
					    putpixel( k,j,WHITE );
					else
					    putpixel( k,j,GREEN);
			}
       }
	}
}
 
 
int main()
{
	Draw();
	change();
	getch();
	return 0;
}

运行截图：

(2)旋转.由键盘输入旋转角度和旋转中心;

#include 
#include 
#include 
#include 
//f[20][2]中存放的是飞机的关键点
int f[15][2] = 
{285,70,310,100,310,185,430,240,440,260,310,225,310,355,345,400,225,400,260,355,260,225,130,260,140,240,260,185,260,100};
int b;
float k;
int n = 15;
int a[15][2];
void DDALine( int x0,int y0,int x1,int y1 )
{
    //DDA画直线算法
	int dx,dy,epsl,k;
	float x,y,xIncre,yIncre;
	dx = x1 - x0;
	dy = y1 - y0;
	x = x0;
	y = y0;
	if( abs(dx) > abs(dy) )
        epsl = abs(dx);
    else
        epsl = abs(dy);
	xIncre = (float)dx / (float)epsl;
	yIncre = (float)dy / (float)epsl;
	for( k = 0; k <= epsl; k++ )
	{
		putpixel((int)(x+0.5),(int)(y+0.5),GREEN);
		x += xIncre;
		y += yIncre;
	}
 
}
void Rotate()
{
	int i,j,d,p,q;
	int gdriver = DETECT,gmode;
    printf("请输入旋转度数:");
	scanf("%d",&d);
	printf("\n请输入旋转中心:");
	scanf("%d %d",&p,&q);
       	for( i = 0; i < n; i++ )
	{
	    //a[i][0]中存的是x
	    //a[i][1]中存的是y
	    a[i][0] = (f[i][0] - p) * cos(d*1.0) - (f[i][1] - q) * sin(d*1.0) + p;
	    a[i][1] = (f[i][0] - p) * sin(d*1.0) + (f[i][1] - q) * cos(d*1.0) + q;
    }
	initgraph( 960,540 );
	for( j = 0; j < 1000; j++ )
		for( i = 0; i < 1000; i++ )
            putpixel( i,j,WHITE );//首先生成一个960*540大小的窗口，并置成白色
	for( i = 0; i < n - 1; i++ )
        //DDA画直线，首先将飞机的点顺时针按序连成线
		DDALine( a[i][0],a[i][1],a[i+1][0],a[i+1][1] );
	DDALine( a[0][0],a[0][1],a[n-1][0],a[n-1][1] );
}
 


void change()
{
	int i,j,k,s,dx,dy,temp;
	int x0,y0,x1,y1,x2,y2;
	for( i = 0; i < n; i++ )
	{
		if( i == n - 1 )
		{
			x0 = a[i][0];
			y0 = a[i][1];
			x1 = a[0][0];
			y1 = a[0][1];
		}
		else
		{
			x0 = a[i][0];
			y0 = a[i][1];
			x1 = a[i+1][0];
			y1 = a[i+1][1];
		}
		dx = x0 - x1;
		dy = y0 - y1;
		if( y0 > y1 )
		{
			temp = x0;
              x0 = x1;
			  x1 = temp;
            temp = y0;
			  y0 = y1;
			  y1 = temp;
		}
		for( j = y0; j < y1; j++ )
		{
			s = int( (j - y0) * dx / dy ) + x0;//求交点坐标
			for( k = s; k < 1000; k++ )
			{
					if( getpixel( k,j ) == WHITE )
                        putpixel( k,j,BLACK);
					else if( getpixel(k,j) == BLACK)
					    putpixel( k,j,WHITE );
					else
					    putpixel( k,j,GREEN);
			}
       }
	}
}
 
 
int main()
{
	Rotate();
	change();
	getch();
	return 0;
}

运行截图：

2．编码实现Cohen-Sutherland端点编码算法（用矩形窗口裁剪一条直线段）
（选做）关于任意一条水平线（或垂直线）对称
(选做) 任意画出一个多边形，由用户确定一个矩形裁剪窗口的位置和大小,保留窗口里的图形,抹去其余部分;

#include 
#include 
#include 
#define LEFT 1//0001
#define RIGHT 2//0010
#define BOTTOM 4//0100
#define TOP 8//1000
int XL = 100,XR = 400,YB =300,YT = 100;
int encode(int x,int y)
{ 
     int c=0;
	 if(x<XL) c=c|LEFT;
	 else if(x>XR) c=c|RIGHT;
	 if(y>YB) c=c|BOTTOM;
	 else if(y<YT) c=c|TOP;
	 return c;
}
 
// 使用中点算法画任意斜率的直线（包括起始点，不包括终止点）
void DisplayLine(int x1, int y1, int x2, int y2, int color)
{
	int x = x1, y = y1;
	int a = y1 - y2, b = x2 - x1;//a,b分别为x和y的增量
	//考虑四种情况，分别计算增量
	int cx = (b >= 0 ? 1 : (b = -b, -1));
	int cy = (a <= 0 ? 1 : (a = -a, -1));
 
	putpixel(x, y, color);
 
	int d, d1, d2;
	if (-a <= b)		// 斜率绝对值 <= 1
	{
		d = 2 * a + b;
		d1 = 2 * a;
		d2 = 2 * (a + b);
		while(x != x2)
		{
			if (d < 0)
				y += cy, d += d2;
			else
				d += d1;
			x += cx;
			putpixel(x, y, color);
		}
	}
	else				// 斜率绝对值 > 1
	{
		d = 2 * b + a;
		d1 = 2 * b;
		d2 = 2 * (a + b);
		while(y != y2)
		{
			if(d < 0)
				d += d1;
			else
				x += cx, d += d2;
			y += cy;
			putpixel(x, y, color);
		}
	}
}
 
//画裁剪区域：Breasenham方法和中点画线法均不能画出该裁剪区域
void DisplayRec(int x1,int y1,int x2,int y2,int color){
    DisplayLine(x1,y1,x2,y1,color);
	DisplayLine(x2,y1,x2,y2,color);
	DisplayLine(x2,y2,x1,y2,color);
	DisplayLine(x1,y2,x1,y1,color);
}
 
 
//直线裁剪算法
void Cohen_Sutherland(int x1,int y1,int x2,int y2,int XL,int XR,int YB,int YT)
{ 
   int code1,code2,code;
   int x,y;
   code1=encode(x1,y1);//对端点P1进行编码
   code2=encode(x2,y2);//对端点P2进行编码
   while(code1!=0||code2!=0)
   {
       //相交不为0,第二种情况，全舍去
      if((code1&code2)!=0) return;//整条直线段都在窗口外侧，故简弃
	  code=code1;
	  if(code==0) code=code2;//如果P1点在窗口内,则将code2赋给code，然后判断P2点的位置
	  if((LEFT&code)!=0)//线段与左边界相交
	  {  //根据三角形相似的知识求出P1P2直线段与左边界的交点
	     x=XL;
		 y=y1+(y2-y1)*(XL-x1)/(x2-x1);
	  }
	  else if((RIGHT&code)!=0)//线段与右边界相交
	  {  //根据三角形相似的知识求出P1P2直线段与右边界的交点
	     x=XR;
		 y=y1+(y2-y1)*(XR-x1)/(x2-x1);
	  }
	   else if((BOTTOM&code)!=0)//线段与下边界相交
	  {  //根据三角形相似的知识求出P1P2直线段与下边界的交点
	     y=YB;
		 x=x1+(x2-x1)*(YB-y1)/(y2-y1);
	  }
	   else if((TOP&code)!=0)//线段与上边界相交
	  {  //根据三角形相似的知识求出P1P2直线段与上边界的交点
	     y=YT;
		 x=x1+(x2-x1)*(YT-y1)/(y2-y1);
	  }
	   if(code==code1){
	      x1=x;
		  y1=y;
		  code1=encode(x,y);
	   }
	   else{
	      x2=x;
		  y2=y;
		  code2=encode(x,y);
	   }
   }
   DisplayLine(x1,y1,x2,y2,RED);
   return;
}
 
 
int main()
{
	initgraph(800,800);//根据测试结果初始化图形界面
 
 
	//画裁剪区域
	DisplayRec(XL,YT,XR,YB,GREEN);
 
 
	//裁剪直线
	DisplayLine(380,30,500,245,BLUE);
	Cohen_Sutherland(380,30,500,245,100,400,300,100);//全部区域外
 
   Cohen_Sutherland(250,200,350,250,100,400,300,100);//区域内
 
   DisplayLine(60,250,300,160,WHITE);
Cohen_Sutherland(60,250,300,160,100,400,300,100);//部分区域内
 
    // 按任意键退出
	getch();
	closegraph();
 
	return 0;
}

运行截图：

【小结或讨论】
在制作飞机的过程中，关键点的确定非常重要，否则画出的图形是奇形怪状的。在这个实验中，运用了DDA算法将飞机的关键点连接成线，然后用动态填充算法对飞机进行填充，在此过程中，还要对飞机进行比例缩放，为了减少代码，就是直接求的放大倍数（小于1也是可以的）。紧接着是让飞机进行旋转，此时需要输入旋转角度和旋转中心，这就需要对图形的变换有着较为深刻地理解。特别注意的是，整个显示屏都是以屏幕左上角作为坐标原点，实验中由于没有意识到这个问题，犯了一些错误。
第二个实验是编码实现Cohen-Sutherland端点编码算法（用矩形窗口裁剪一条直线段），这个实验我们首先要确定一个窗口，然后对各个不同方向编码，在这个实验中采取了中点算法画任意斜率的直线，对直线的两个端点编码，判断与窗口的位置关系。根据直线与窗口是否有交点以及交点的位置判断是否对直线进行裁剪，在主函数中，我设置了三种不同位置的直线，以便观察直线与窗口的位置关系。同样要注意的是，屏幕左上角才是坐标原点。