The 2022 ICPC Asia Regionals Online Contest (II) 2022ICPC第二场网络赛 ABEFGJKL题解
文章目录
- A Yet Another Remainder【费马小定理】
- B Non-decreasing Array【线性DP】
- E An Interesting Sequence【签到】
- F Infinity Tree 【签到】
- G Good Permutation【排列组合,树形结构】
- J A Game about Increasing Sequences【博弈】
- K Black and White Painting【模拟】
- L Quadruple【简单容斥】
A Yet Another Remainder【费马小定理】
首先明确x是无法求解的,当x大于1e6,一共有1e4个方程组,不可能求解1e6个未知数。
因为题目将x的各个十进制位拆开,并且按照不同的步长分组,因此可能是通过计算组内的值,再将各组的值拼接起来得到 x m o d p x\ mod\ p x mod p的结果。
p p p都是小于100的数, m o d p mod\ p mod p的结果必然都是100以内的值,因此推测 m o d p mod\ p mod p的结果可能会产生某种规律,比如形成循环节出现。
到这里没有什么新的思路,因此可以翻翻书找找跟质数和模数有关的定理来辅助解题…最常见最相关的就是费马小定理了!
费马小定理: 如果p是一个质数,而整数a不是p的倍数,则有 a ( p − 1 ) ≡ 1 a^{(p-1)}≡1 a(p−1)≡1(mod p)。
费马小定理中的 p p p就是我们题目中的 p p p,那么 a a a可以是什么呢?题目将 x x x按照10进制进行拆分,因此 a a a可以是 1 0 i 10^i 10i,可惜发现 p = 5 p=5 p=5时 1 0 i 10^i 10i是5的倍数,但是!题目非常细心地将 p = 5 p=5 p=5的情况给剔除掉了!因此可以确定这个方向应该是正确的!
接下来就是利用费马小定理给 x m o d p x\ mod\ p x mod p进行分组求和了。因为 1 0 p − 1 ≡ 1 ( m o d p ) 10^{p-1}≡1(mod\ p) 10p−1≡1(mod p),因此有 1 0 2 ( p − 1 ) ≡ ( m o d p ) , 1 0 3 ( p − 1 ) ≡ ( m o d p ) . . . 1 0 s ( p − 1 ) ≡ ( m o d p ) 10^{2(p-1)}≡(mod\ p),\ 10^{3(p-1)}≡(mod\ p)...\ 10^{s(p-1)}≡(mod\ p) 102(p−1)≡(mod p), 103(p−1)≡(mod p)... 10s(p−1)≡(mod p),其中s表示最后一项。因此可以将 1 0 k ( p − 1 ) ≡ 1 ( m o d p ) 10^{k(p-1)}≡1(mod\ p) 10k(p−1)≡1(mod p)当成一组同时求解。而在第 p − 1 p-1 p−1行,给定的恰好是以 p − 1 p-1 p−1为步长的十进制位的和。
因为 x = 1 0 n − 1 ∗ a 1 + 1 0 n − 2 ∗ a 2 + . . . + 1 0 n − i ∗ a i + 1 0 0 ∗ a n x=10^{n-1}*a^1+10^{n-2}*a^2+...+ 10^{n-i}*a^i+10^0*a^n x=10n−1∗a1+10n−2∗a2+...+10n−i∗ai+100∗an,可知找到 1 0 s ( p − 1 ) 10^{s(p-1)} 10s(p−1)对应的是a数组的第 n − s ( p − 1 ) n-s(p-1) n−s(p−1)项,即 b p − 1 , n − s ( p − 1 ) b_{p-1,n-s(p-1)} bp−1,n−s(p−1)。
将 1 0 k ( p − 1 ) + 1 , k = 0 , 1 , 2 , . . . , s 10^{k(p-1)+1},\ k=0,1,2,...,s 10k(p−1)+1, k=0,1,2,...,s的项作为一组,将 1 0 k ( p − 1 ) + 2 , k = 0 , 1 , 2 , . . . , s 10^{k(p-1)+2},\ k=0,1,2,...,s 10k(p−1)+2, k=0,1,2,...,s作为一组。
即将x拆解为 ( a 1 + a 1 + ( p − 1 ) + a 1 + 2 ( p − 1 ) + . . . + a 1 + s ( p − 1 ) ) ∗ 1 0 ( n − 1 ) % ( p − 1 ) ) + ( a 2 + a 2 + ( p − 1 ) + a 2 + 2 ( p − 1 ) + . . . + a 2 + s ( p − 1 ) ) ∗ 1 0 ( n − 2 ) % ( p − 1 ) ) + . . . + ( a p − 1 + a p − 1 + ( p − 1 ) + a p − 1 + 2 ( p − 1 ) + . . . + a p − 1 + s ( p − 1 ) ) ∗ 1 0 ( n − p + 1 ) % ( p − 1 ) ) (a_1+a_{1+ (p-1)}+a_{1+2(p-1)}+...+a_{1+s(p-1)})*10^{(n-1)\%(p-1)})+\\(a_2+a_{2+ (p-1)}+a_{2+2(p-1)}+...+a_{2+s(p-1)})*10^{(n-2)\%(p-1)})+\\...+\\(a_{p-1}+a_{p-1+ (p-1)}+a_{p-1+2(p-1)}+...+a_{p-1+s(p-1)})*10^{(n-p+1)\%(p-1)}) (a1+a1+(p−1)+a1+2(p−1)+...+a1+s(p−1))∗10(n−1)%(p−1))+(a2+a2+(p−1)+a2+2(p−1)+...+a2+s(p−1))∗10(n−2)%(p−1))+...+(ap−1+ap−1+(p−1)+ap−1+2(p−1)+...+ap−1+s(p−1))∗10(n−p+1)%(p−1))
用b表示为 b p − 1 , 1 ∗ 1 0 ( n − 1 ) % ( p − 1 ) + b p − 1 , 2 ∗ 1 0 ( n − 2 ) % ( p − 1 ) + . . . + b p − 1 , p − 1 ∗ 1 0 ( n − p + 1 ) % ( p − 1 ) b_{p-1,1}*10^{(n-1)\%(p-1)}+b_{p-1,2}*10^{(n-2)\%(p-1)}+...+b_{p-1,p-1}*10^{(n-p+1)\%(p-1)} bp−1,1∗10(n−1)%(p−1)+bp−1,2∗10(n−2)%(p−1)+...+bp−1,p−1∗10(n−p+1)%(p−1)
#includeB Non-decreasing Array【线性DP】
赛时没过题,一直往区间dp想,复杂度是 n 4 n^4 n4的,很难优化。但是dp最简单的就是从头到尾推的线性dp啊…下次思路卡住就看看书吧!dp入门!
先简单地证明一下,将一个数字删除总是会得到更好的结果
假设现在的数组是 a , b , c ( c > = b > = a ) a,b,c(c>=b>=a) a,b,c(c>=b>=a),三个数对答案的贡献是 ( c − b ) 2 + ( b − a ) 2 (c-b)^2+(b-a)^2 (c−b)2+(b−a)2,而将中间的数删除之后,对答案的贡献变成 ( c − a ) 2 = ( ( c − b ) + ( b − a ) ) 2 = ( c − b ) 2 + ( b − a ) 2 + 2 ( c − b ) ( b − a ) (c-a)^2=((c-b)+(b-a))^2=(c-b)^2+(b-a)^2+2(c-b)(b-a) (c−a)2=((c−b)+(b−a))2=(c−b)2+(b−a)2+2(c−b)(b−a),因为 c > = b , b > = a c>=b,b>=a c>=b,b>=a,因此每删除一个中间数,答案就相比原来增加2*中间数与前数的差*后数与前数的差。删除一个数,答案增加如上所述,而改变一个数,其实最佳方式就是直接将其变成它的某个相邻数,因为相邻差变为0,对答案不再有贡献,其实和删除的操作是一样的。因此第 k k k次操作,就是选两个数删除掉。
先记录起始的答案,接下来只有相邻差有用,而原来的数已经没有用了,因此直接记录它们的相邻差数组 d i f dif dif即可。接下来的问题就像石子合并:一开始有 n − 1 n-1 n−1堆石子,每堆石子的数量为 d i f [ i ] dif[i] dif[i],每次选择相邻的两堆石子 i , j i,j i,j,答案增加 2 ∗ d i f [ i ] ∗ d i f [ j ] 2*dif[i]*dif[j] 2∗dif[i]∗dif[j],然后将两堆石子合并起来。
f [ i ] [ j ] f[i][j] f[i][j]表示从第一堆石子到第 i i i堆石子,已经合并了 j j j堆石子获得的最大答案。
接下来思考如何更新 f [ i ] [ j ] f[i][j] f[i][j]。只需要考虑最后第 i i i堆和前面多少堆连续合并在一起即可。
- 第 i i i堆不合并,直接从 f [ i − 1 ] [ j ] f[i-1][j] f[i−1][j]更新过来。
- 第 i i i堆只和第 i − 1 i-1 i−1合并,答案为 f [ i − 2 ] [ j − 1 ] f[i-2][j-1] f[i−2][j−1]再加上第 i i i堆和第 i − 1 i-1 i−1堆合并的新答案。
- 第 i i i堆和第 i − 1 , i − 2 i-1,i-2 i−1,i−2堆合并,一共合并2次,答案为 f [ i − 3 ] [ j − 2 ] f[i-3][j-2] f[i−3][j−2]再加上后面三堆合并的新答案。
依次类推即可。
note: 可预处理出数组 g [ i ] [ j ] g[i][j] g[i][j]表示从 i i i到 j j j连续段石子合并的答案。
#includeE An Interesting Sequence【签到】
找到第一个和k互质的数,然后一直放2323…或者3232…即可。
F Infinity Tree 【签到】
观察发现,第n秒树的大小为 ( k + 1 ) n (k+1)^n (k+1)n,不难推出,节点x的父亲节点为 ( x − t − 1 ) / k + 1 (x - t - 1) / k + 1 (x−t−1)/k+1,其中 t t t为第一个小于x的 ( k + 1 ) n (k+1)^n (k+1)n,每次暴力找到第一个小于x和小于y的节点,一直往上跳即可。
G Good Permutation【排列组合,树形结构】
考虑最简单的情况,只有 [ 1 , n ] [1,n] [1,n]一个区间,答案就是 n ! n! n!。如果 [ 1 , n ] [1,n] [1,n]中包含 3 3 3个区间限制,恰好覆盖 [ 1 , n ] [1,n] [1,n]整个区间,长度分别为 l e n 1 , l e n 2 , l e n 3 len1,len2,len3 len1,len2,len3,答案是 3 ! ∗ l e n 1 ! ∗ l e n 2 ! ∗ l e n 3 ! 3!*len1!*len2!*len3! 3!∗len1!∗len2!∗len3!。 3 ! 3! 3!表示将3个限制区间在 [ 1 , n ] [1,n] [1,n]之间进行全排列, l e n 1 ! len1! len1!表示被分到第1个区间的连续数字的排列方案。但是如果区间1还有2个小区间,长度分别为 l e n 11 , l e n 12 len11,len12 len11,len12,这时区间1的方案数就变成 2 ! ∗ l e n 11 ! ∗ l e n 12 2!*len11!*len12 2!∗len11!∗len12,全区间的方案数也会从 3 ! ∗ l e n 1 ! ∗ l e n 2 ! ∗ l e n 3 ! 3!*len1!*len2!*len3! 3!∗len1!∗len2!∗len3!变成 3 ! ∗ 2 ! ∗ l e n 11 ! ∗ l e n 12 ∗ l e n 2 ! ∗ l e n 3 ! 3!*2!*len11!*len12*len2!*len3! 3!∗2!∗len11!∗len12∗len2!∗len3!。因此应该先将小区间更新,更新完小区间再用小区间更新大区间。
因为每个区间只有包含和并列关系,因此构成了树形结构,可以给每个区间一个编号。然后排序乱搞一通获得一棵树结构。先利用set将区间去重,然后按照左端点从小到大,右端点从大到小排序。这样排序可保证后面的区间必然不是前面的区间的父亲,因此每次记录上一次排序结束的区间节点 p r e pre pre,当前区间的节点为 c u r cur cur,则 c u r cur cur的父亲就是 c u r cur cur和 p r e pre pre的最近公共祖先,因为 p r e pre pre和 c u r cur cur区间中间已经没有隔着其他区间了。
#includeJ A Game about Increasing Sequences【博弈】
可以发现,只有数列从左向右最长的一段递增序列和从右向左最长的一段递增序列有用。
考虑这两段序列的起始元素,如果两个元素大小相同,且两段序列中存在一段奇数长度的序列则先手必胜。
否则:
如果大的那个元素对应的序列长度为奇数,那么先手必胜;
不然先手必然选小的那个元素,然后轮到后手选;
我们直接模拟一遍即可得出结果。
K Black and White Painting【模拟】
因为整个网格的大小只有200*200,因此考虑标记每个网格的有贡献的边和圆弧来统计答案。用左下角的点来表示网格。对于每个网格,直线边有上下左右四条边,网格内可能存在四种圆弧。因此只需要考虑边和圆弧的所有组合情况即可。
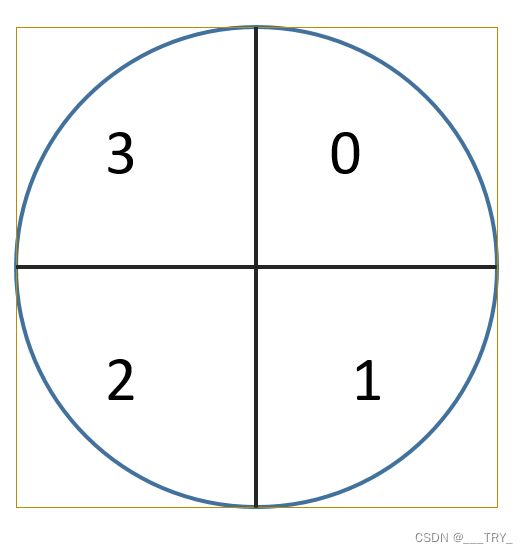
-
若整个网格都某个正方形覆盖,那么不管网格里的所有圆弧都会失效,枚举网格四条边看是否存在一条正方形边,且不会被其他的图形覆盖。比如判断网格左边是否有贡献,要检查:网格左侧有正方形边,当前网格左侧的网格没有整个网格被覆盖且没有23形状的圆弧。
-
存在两段圆弧(除了02组合和13组合的其他圆弧组合情况),都会有1/3的圆弧贡献
-
存在一段圆弧,都会有1/2的圆弧贡献。
#include<bits/stdc++.h>
using namespace std;
const int N = 210, mod = 998244353;
bool a[N][N], b[N][N][4], c[N][N][2];
int qpow(int a, int b)
{
int ans = 1;
while(b)
{
if(b & 1) ans = 1ll * ans * a % mod;
a = 1ll * a * a % mod;
b >>= 1;
}return ans;
}
bool ckl(int i, int j){return (!a[i][j - 1] && !b[i][j - 1][2] && !b[i][j - 1][3]) && c[i][j][0];}
bool ckr(int i, int j){return (!a[i][j + 1] && !b[i][j + 1][0] && !b[i][j + 1][1]) && c[i][j + 1][0];}
bool cku(int i, int j){return (!a[i - 1][j] && !b[i - 1][j][0] && !b[i - 1][j][3]) && c[i - 1][j][1];}
bool ckd(int i, int j){return (!a[i + 1][j] && !b[i + 1][j][1] && !b[i + 1][j][2]) && c[i][j][1];}
int main()
{
int n; cin >> n;
for(int i = 1; i <= n; i ++)
{
int op, x, y; cin >> op >> x >> y;
x += 102, y += 102;
if(op == 1)
a[x][y] = a[x + 1][y] = a[x + 1][y - 1] = a[x][y - 1] = true,
c[x][y - 1][0] = c[x][y + 1][0] = c[x + 1][y - 1][0] = c[x + 1][y + 1][0] = true,
c[x - 1][y - 1][1] = c[x - 1][y][1] = c[x + 1][y - 1][1] = c[x + 1][y][1] = true;
else b[x][y][0] = b[x + 1][y][1] = b[x + 1][y - 1][2] = b[x][y - 1][3] = true;
}
int r1 = 0, r2 = 0;
for(int i = 1; i < N - 1; i ++)
{
for(int j = 1; j < N - 1; j ++)
{
if((b[i][j][0] && b[i][j][2]) || (b[i][j][1] && b[i][j][3])) continue;
else if(a[i][j]) r1 += ckl(i, j) + ckr(i, j) + cku(i, j) + ckd(i, j);
else if((b[i][j][0] || b[i][j][2]) && (b[i][j][1] || b[i][j][3])) r2 += 2;
else if(b[i][j][0] || b[i][j][1] || b[i][j][2] || b[i][j][3]) r2 += 3;
}
}
printf("%d %d\n", r1, 1ll * r2 * qpow(6, mod - 2) % mod);
return 0;
}
L Quadruple【简单容斥】
首先不难想到处理出ICPC的前缀和来对付区间询问,但是这样会算多一些,因为区间外的I与区间内的CPC组成的ICPC、区间外的IC和区间内的PC组成的ICPC和区间外的ICP和区间内的C组成的ICPC都会被算进去。于是我们减掉这些即可。CPC的方案数和PC的方案数计算方法也是类似的。
#include