2021年蓝桥杯省赛JavaB组真题解析

距离蓝桥杯省赛还有1个多月，为了拿到更好地成绩，让我们刷起来。

一：填空题

1. ASC

已知大写字母 A 的 ASCII 码为 65，请问大写字母 L 的 ASCII 码是多少？

分析：签到题。看到这题的时候会想，这题咋这么简单，直接计算就行，都不需要写程序。实际上，在蓝桥杯省赛中，填空题的前两题和编程题的第一题都是签到题，比较简单。但同时，这也是我们要想尽办法拿下来的题目，因此一定要细心，细心，再细心。同时，我建议简单的题也最好是编程解决或者用计算器计算，毕竟考试的时候紧张的话还是有可能算错最基本的运算的。

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        System.out.println((int)'L');
    }
}

输出答案：

76

注意：填空题只需要填最后的答案即可，因此可采取所有得到答案的方法。暴力+合理利用工具。

2. 卡片

小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。 小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个， 就保存起来，卡片就不能用来拼其它数了。 小蓝想知道自己能从 1 拼到多少。 例如，当小蓝有 30张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10， 但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。 现在小蓝手里有 0到 9的卡片各 2021 张，共 20210 张，请问小蓝可以从 1拼到多少？ 提示：建议使用计算机编程解决问题

分析：从1开始遍历，判断遍历到的数可否用目前的卡片拼出来，可以的话，继续遍历，否则输出答案（答案为现在遍历到的数减1）。

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int[] arr = new int[10];
        Arrays.fill(arr, 2021);
        for(int i = 1;;i++){
          int temp = i;
          while(temp > 0){
            int r = temp % 10;
            if(arr[r] > 0){
              arr[r]--;
            }
            else{
              break;
            }
            temp /= 10;
          }
          if(temp > 0){
            System.out.println(i - 1);
            break;
          }
        }
        scan.close();
    }
}

输出答案：

3181

对于这道题，如果想要验证自己得到的答案是否正确的话。可以修改一下程序，主动输入一个n，n表示有0到9的卡片各n张，然后输入3，如果输出的是10，则意味着自己的计算是正确的。

3. 直线

在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，
那么这些点中任意两点确定的直线是同一条。
给定平面上 2 × 3 个整点 {(x,y)|0 ≤ x < 2,0 ≤ y < 3, x ∈ Z,y ∈ Z}，即横坐标
是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数
的点。这些点一共确定了 11 条不同的直线。
给定平面上 20 × 21 个整点 {(x,y)|0 ≤ x < 20,0 ≤ y < 21, x ∈ Z,y ∈ Z}，即横
坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之
间的整数的点。请问这些点一共确定了多少条不同的直线。

分析：枚举两个不同的点，两点确定一条直线。具体的，直线由y=kx+b表示，看有多少种（k,b）的组合。但由于k和b都是浮点数，Java中是不能够通过==直接判断两个浮点数是否相等的，为此我们用"(b2 - b1) / (a2 - a1) (b1 * (a2 - a1) - a1 * (b2 - b1) / (a2 - a1))"字符串的形式表示一根直线。然后通过Set集合去重，自定义的类需要通过重写equals方法和hashCode()方法才能被Set集合去重。

import java.util.*;
public class Main {
	public static void main(String[] args) {
		Set<String> ans = new HashSet<String>();
		for(int a1 = 0; a1 <= 19; a1++) {
			for(int b1 = 0; b1 <= 20; b1++) {
				for(int a2 = 0; a2 <= 19; a2++) {
					for(int b2 = 0; b2 <= 20; b2++) {
                        // 斜率不存在和斜率为0的特殊情况，我们可以手动计算无需特殊判断
						if(a1 == a2 || b1 == b2) {
							continue;
						}
                        // 以分子/分母的形式表达斜率k和截距b时，分子和分母需要是最简的形式
						StringBuilder sb = new StringBuilder();
						int up = b2 - b1;
						int down = a2 - a1;
						int r = gcd(up, down);
						sb.append(up / r + " ");
						sb.append(down / r + " ");
						up = b1 * down - a1 * up;
						r = gcd(up, down);
						sb.append(up / r + " ");
						sb.append(down / r);
						ans.add(sb.toString());
					}
				}
			}
		}
        // 斜率不存在的直线20根，斜率为0的直线21根
		System.out.println(ans.size() + 20 + 21);
	}
	static int gcd(int a, int b) {
		return b == 0 ? a : gcd(b, a % b);
	}
}

输出：

40257

4. 货物摆放

现在，小蓝有 n箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、宽、高。

小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足n=L×W×H。

给定 n，请问有多少种堆放货物的方案满足要求。

例如，当 n = 4 时，有以下 6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1。

请问，当 n = 2021041820210418（注意有 16位数字）时，总共有多少种方案？

提示：建议使用计算机编程解决问题。

分析：给出一个数n，求多少个三元组（L，W，H）使得L x W x H等于n。同时三元组是考虑顺序的，L，W，H是n的因数，即n % L == 0 && n % W == 0 && n % H == 0，为此，我们可以先将n的所有因数求出来，然后三重循环遍历L,W,H，若它们相乘等于n，则找到了一种方案。（暴力）

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
      // 常数默认值为int，告诉编译器它是long型常量
      long n = 2021041820210418l;
      int ans = 0;
      List<Long> l = new ArrayList<>();
      for(long i = 1; i <= Math.sqrt(n); i++){
        if(n % i == 0){
          l.add(i);
          if(i != n / i){
            l.add(n / i);
          }
        }
      }
      for(int i = 0; i < l.size(); i++){
        for(int j = 0; j < l.size(); j++){
          if(l.get(i) * l.get(j) > n){
            continue;
          }
          for(int k = 0; k < l.size(); k++){
            if(l.get(i) * l.get(j) * l.get(k) == n){
              ans++;
            }
          }
        }
      }
      System.out.println(ans);
    }
}

输出答案：

2430

5. 路径

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图 中的最短路径。

小蓝的图由 2021 个结点组成，依次编号 1 至 2021。

对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点 之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。

例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无 向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。

请计算，结点 1 和结点 2021 之间的最短路径长度是多少。

提示：建议使用计算机编程解决问题。

分析：题目意思很明确，求源点到某个点的最短路径。最短路问题有两个常见的算法，Dijkstra算法和Floyed算法。本题适合用Dijkstra算法，为此我们先建图，图用二维矩阵e存储，dist数组表示源点到某个点的最短距离。最后输出dist[2021]的值。

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        int[][] e = new int[2022][2022];
        int[] dist = new int[2022];
        boolean[] visit = new boolean[2022];
        Arrays.fill(dist, Integer.MAX_VALUE);
        for(int i = 1; i <= 2021; i++){
          for(int j = 1; j <= 2021; j++){
            if(i == j){
              e[i][j] = 0;
            }
            else{
              if(Math.abs(i - j) <= 21){
                e[i][j] = i * j / gcd(i, j);
              }
              else{
                e[i][j] = Integer.MAX_VALUE;
              }
            }
          }
        }
        dist[1] = 0;
        for(int i = 1; i <= 2021; i++){
          int u = 0, min = Integer.MAX_VALUE;
          for(int j = 1; j <= 2021; j++){
            if(!visit[j] && dist[j] < min){
              min = dist[j];
              u = j;
            }
          }
          visit[u] = true;
          for(int j = 1; j <= 2021; j++){
            if(e[u][j] != Integer.MAX_VALUE && dist[u] + e[u][j] < dist[j]){
              dist[j] = dist[u] + e[u][j];
            }
          }
        }
        System.out.println(dist[2021]);
    }
    static int gcd(int a, int b){
      return b == 0 ? a : gcd(b, a % b);
    }
}

输出答案：

10266837

二：编程题

6. 时间显示

题目描述

小蓝要和朋友合作开发一个时间显示的网站。

在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 19701970 年 11 月 11 日 00:00:0000:00:00 到当前时刻经过的毫秒数。

现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。

给定一个用整数表示的时间，请将这个时间对应的时分秒输出。

输入描述

输入一行包含一个整数，表示时间。

输出描述

输出时分秒表示的当前时间，格式形如 HH:MM:SS，其中 HH 表示时，值为 00 到 2323，MM 表示分，值为 00 到 5959，SS 表示秒，值为 00 到 5959。时、分、秒 不足两位时补前导 00。

输入输出样例

示例 1

输入

46800999

输出

13:00:00

示例 2

输入

1618708103123

输出

01:08:23

评测用例规模与约定

对于所有评测用例，给定的时间为不超过 10的18次方的正整数。

运行限制

• 最大运行时间：1s
• 最大运行内存: 512M

分析：签到题，注意1s=1000ms，先将ms转化为s，即n/1000(采用整除)。对于这一题，需理解取余的含义，即不需要知道它经历了多少年，算出它对于60s一分钟剩了多少秒，对于60min一小时剩了多少分钟，24h一天剩余了多少小时即可，剩余多少用取余表示。

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        long n = scan.nextLong();
        n /= 1000;
        // 1s = 1000ms
        // 1min = 60s = 60000ms
        // 1h = 60min = 3600s = 3600000ms
        System.out.printf("%02d:%02d:%02d", (n % (3600 * 24)) / 3600,(n % 3600) / 60,n % 60);
        scan.close();
    }
}

7. 最少砝码

问题描述

你有一架天平。现在你要设计一套砝码，使得利用这些砝码可以称出任意 小于等于 N的正整数重量。

那么这套砝码最少需要包含多少个砝码？

注意砝码可以放在天平两边。

输入格式

输入包含一个正整数 N。

输出格式

输出一个整数代表答案。

样例输入

7

样例输出

3

样例说明

33 个砝码重量是 1、4、6，可以称出 1 至 7的所有重量。

1 = 1;

2 = 6 − 4(天平一边放 66，另一边放 44)；

3 = 4 − 1;

4 = 4；

5 = 6 − 1；

6 = 6；

7 = 1 + 6；

少于 3 个砝码不可能称出 1 至 7 的所有重量。

评测用例规模与约定

对于所有评测用例，1 ≤ N ≤ 1000000000。

运行限制

• 最大运行时间：1s
• 最大运行内存: 512M

分析：思维题吧，如果以前没做过的话估计是想不到的，反正我看到之后第一反应是懵的。看到有的文章是这样推理的，称取质量1只需一个砝码1，第二个需要称取质量2，这时添加一个砝码1可以和第一个1组成2，添加砝码2除了可以组成2之外还可以组成3，添加砝码3可以组成2,3,4，添加砝码4的话就不能得到质量2因此不行，由贪心的思想第二个砝码还是选取砝码3好，然后可以依次退出规律。

应称重量	选择的砝码(choice)	最终可称到的重量（total)
1	1	1
2	3	4
5	9	13
14	27	40
total+1	choice*3	choice*3 + total

通过上表可以找出规律，而实际上，由首项为1，公比为3的等差数列，可以自由组成任意正整数。

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int n = scan.nextInt();
        int count = 1, now = 1, sum = 1;
        while(sum < n){
          count++;
          now *= 3;
          sum += now;
        }
        System.out.println(count);
        scan.close();
    }
}

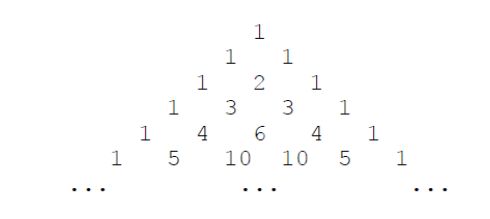
8. 杨辉三角形

下面的图形是著名的杨辉三角形：

如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列： 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ⋯

给定一个正整数 N，请你输出数列中第一次出现 N是在第几个数？

输入描述

输入一个整数 N。

输出描述

输出一个整数代表答案。

输入输出样例

示例 1

输入

6

输出

13

评测用例规模与约定

对于 20% 的评测用例，1≤N≤10； 对于所有评测用例，1≤N≤1000000000。

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

分析：又是偏思维的题，这还是大家所讨论的暴力杯吗。虽然考试的时候，我们可能想不到能够AC的代码，但一定不能留空白，哪怕写的是纯暴力的代码也给它交上去，蓝桥杯是按点给分的（总共10个计分点），而且题目这不是明显的暗示吗——对于 20% 的评测用例，1≤N≤10。好了进入正题，杨辉三角实际上就是一个排列组合的表格。要是数据少的话我们还能通过极限打表给它打出来，但题目给出的n的最大值有10的9次方，为此我们需要尽可能的优化，毕竟优化之后可能又能多过一个点呢。优化第一步：从图中可以看出，每一行左边的数与右边的数对称，因此在遍历的时候，我们可以只遍历左边的图，且最大值第一次出现一定是在图的左边。但这样还是AC不了。优化第二步：考虑左边图形的斜行，第0斜行的开始是(C00)，第1斜行的开始是(C21)，第2斜行的开始是(C42)依次第n斜行的开始是(C2nn)，且每一斜行是单调递增的，下面的斜行比上面的斜行大。可以计算到n取最大值也是在第16斜行可以遍历到，因此我们对于输入的n，从第16斜行往第0斜行遍历，直到第一次找到。对于每一斜行采用二分查找。哎，反正我是没想到这么巧妙的方法，长长见识。

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    static int n;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        n = scan.nextInt();
        for(int i = 16;;i--){
          if(check(i)){
            break;
          }
        }
        scan.close();
    }
    static boolean check(int i)
	{
    // 二分该斜行,找到大于等于该值的第一个数
    // 左边界2k，右边界为max(l, n)取二者最大，避免右边界小于左边界
    int r = 2 * i, l = Math.max(n,r);
    while(r < l)
    {
        int mid = (l - r) / 2 + r;
        if(C(mid, i) >= n) l = mid;
        else r = mid + 1;
    }
    if(C(r, i) != n)
        return false;
    else{
    // 1L * (r + 1) * r / 2中这个1L是不能少的，因为r是int类型的，如果没有1L将表达式的值提高到	// long的话，表达式的值会先溢出，这时在强制转化为long没有作用
    System.out.println((long) (1l * (r + 1) * r / 2) + i + 1);
    return true;
    }
}
    static long C(int a, int b){
      long ans = 1;
      for(int i = a, j = 1; j <= b; j++, i--){
        ans = ans * i / j;
        if(ans > n){
            // 避免ans超过long的最大值
          return ans;
        }
      }
      return ans;
    }
}

9. 双向排序

题目链接：https://www.lanqiao.cn/problems/1458/learning/

博客链接：https://blog.csdn.net/qq_35975367/article/details/116277383

说实话看不太懂……

10. 括号序列

题目链接：https://www.lanqiao.cn/problems/1456/learning/

博客链接：https://blog.csdn.net/qq_51972900/article/details/116428039

从上面这套真题可以看出蓝桥杯的题目难易分明，也不是大家口中常说的暴力杯。虽然说确实有签到送分题，但也不会缺少思维题（好难啊），对于思维题是在想不出的话还是暴力拿部分样例分吧……